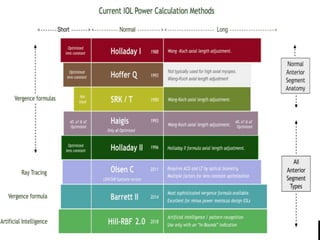
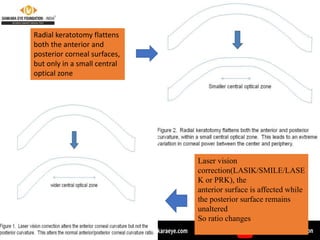
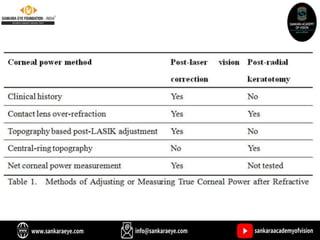
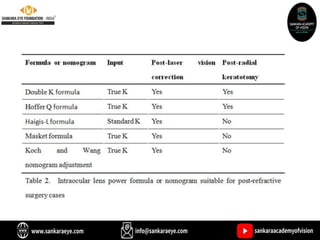
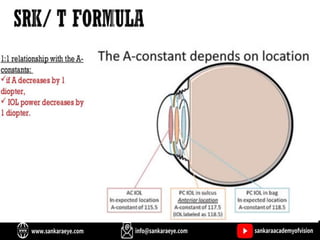
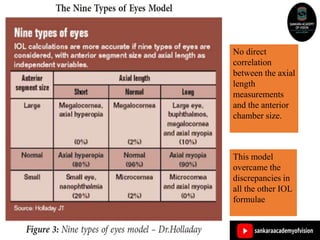
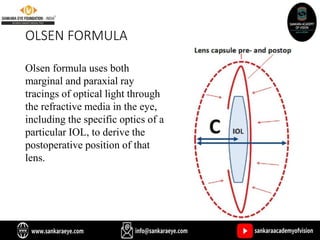
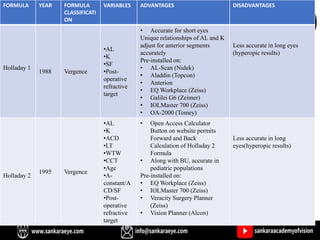
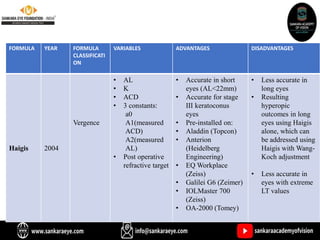
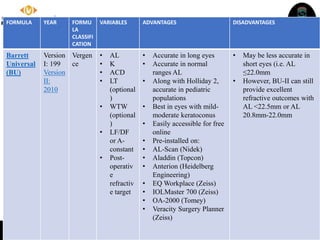
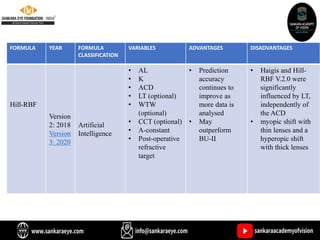
The document discusses various intraocular lens (IOL) calculation formulas used for cataract surgery, detailing their historical development and mathematical foundations. It explores different generations of formulas, including theoretical, regression, and AI-driven methods, highlighting factors affecting effective lens position and the importance of accurate biometric measurements. Additionally, it explains the adaptation of IOL power based on anatomical and surgical factors, ensuring optimal refractive outcomes for patients.

1. Biometry –IOL formulas
and Calculation
Presenter : Dr. Kervi

2. HISTORY-

3. IDEM LENSES
In the 1980s IDEM lenses(ideal emmetropia lenses) with them pre
and post refraction was similar.
• Done in patients who were emmetropic before cataract
development.
• The power of this lens was mathematically deduced to be +17.0 D
for an AC lens
• +19.0D for an iris fixated lens
• +21.0D for a posterior chamber lens.

4. STANDARD LENSES
• The standard lens is approx. 2D stronger than the IDEM lens,
thereby rendering the Pseudophakic eye myopic as compared
to preoperative emmetropic refraction.
• Lens power calculated by adding +1.25D to the calculated
power of an IDEM lens to restore emmetropia.

5. EMMETROPIA LENS
Done in previous ammetropia patients
• To restore the patient to an emmetropic status after cataract surgery
• Take care of pre-existing refractive error
• Power calculated by multiplying the pre existing refractive error
with a conversion factor of 1.25 and algebraically adding it on to
the IDEM lens power (hypermetropia patients)
• Subtracting in myopic patients

6. • For example: if a patient had an axial myopia of 3.0D before the onset
of cataract
• The power of the emmetropia lens may be calculated thus:
3.0 x 1.25 = 3.75
Idem lens power for a Posterior chamber IOL = 21.0D
Emmetropia lens power = 21.0 + (-3.75) = +17.25D

7. DUAL LENS SYSTEM
• The human eye forms a homo centric complex lens system.
The primary or the
objective lens as well as
the distance of the
focusing screen are fixed
– then the effective
power of this system of
lenses will depend on
the power and the
position of the second
lens.

8. SCHEMATIC EYE
• According to GAUSS concept eye can be resolved into 6 cardinal
points

9. LISTINGS REDUCED EYE DONDERS REDUCED EYE

10. GAUSS THEOREM
• For a system of two or more lenses in succession : the image
produced by the first lens acts as an object to the second lens
• The image produced by the second Lens acts as an object for the third
lens and so on.

11. According to the GAUSS
theorem for a system of homo
centric Lens, there exist
three pairs of cardinal points
2 focal points
2 Principal points and
2 nodal points
which are all situated on the
principal axis of the system

13. Having known all the three pairs of
cardinal points of a thick lens, it is easier
to calculate the power of the lens

14. • Using the corneal refractive indices and radius of curvature as given
by Gullstrand, the net corneal power can be derived by applying
Gaussian optics
Da is the anterior corneal power;
Dp is the posterior corneal
power; ra is anterior radius of
curvature of cornea; rp is
posterior radius of curvature of
cornea; Dnet is the total/net
power of cornea

15. PRE-REQUISITES FOR IOL POWER
CALCULATION FORMULA
• 3 Essential parameters needed for accurate IOL power calculation
• 2 Measured parameters- Keratometry measurement of corneal
curvature and Axial Length
• 1 predicted parameter- Post op anterior chamber depth

16. TYPES OF IOL POWER FORMULAE
• Theoretical formulae
• Regression formulae

17. THEORETICAL FORMULAE
• Based on an optical model of the eye
• An optics equation is used to determine the IOL power
• Complex calculations
• Assumptions are made
• Examples of Theoretical formulae- Binkhorst Formula, colenbrander ,
Gill formula

18. • Different theoretical formulae, make different assumptions about,
• Refractive index of the cornea
• Distance of the Cornea to the IOL
• Distance of the IOL to the retina
• All these theoretical equations make simplifying assumptions about
the optics of the eye.
• Therefore they do not provide a perfect prediction of the IOL power.
• Obsolete

19. REGRESSION/EMPIRICAL FORMULAE
• These are based on retrospective analysis of actual post operative
refractive data.
• Large number of IOL implantation plotted with respect to
• Corneal power
• Axial length of the eye
• The best fit equation is then determined by statistical regression
analysis of data

20. • No assumptions are made about the optics of the eye
• The regression equations are only as good as the accuracy of
the data used to derive them
• Example is SRK formula, SRK 2 , Hoffer formula

21. VERGENCE FORMULAE
• Are 3rd and 4th generation formulae which incorporate theoretical and
regression analysis
• Accurate calculation of Effective lens position (ELP) is possible when
both theoretical and regression analysis are combined
• Sub classified based on number of biometry variables
• Holladay 1 , hoffer Q , SRK T , T 2 : 2 variables
• Haigis formula : 3 variables
• Barrett universal 2 : 5variables
• Holladay 2 : 7 variables

22. RAY TRACING FORMULAE
• Individual rays path through different refracting surfaces is traced
• It calculates the postoperative lens position as a fraction of the
crystalline lens thickness and the ACD.
• This allows accurate calculation of lens position
• Prediction of IOL position with C constant
• Example- Olsen formula

23. Ray tracing
formula that
takes in account
both paraxial as
well as marginal
rays of light
entering the eye.

24. ARTICIFICAL INTELLIGENCE
FORMULA
• Researchers in Boston and Los Angeles have developed an artificial
intelligence (AI) neural network to calculate IOL power.
• The Hill-radial basis function (RBF) uses artificial intelligence and
regression analysis of a very large database of actual postsurgical
refractive outcomes to predict the IOL power.

25. • Method of pattern recognition
• If the anatomic characteristics of a particular eye do not match with
many of the eyes in the Hill-RBF database, then the IOL prediction
will be less accurate
• calculator will acknowledge this limitation by showing an out-of-
bounds notification.
• Kane formula incorporates artificial intelligence with theoretical
optics for IOL power prediction

26. A Constant
• A-constant is actually highly variable depending upon multiple
factors
• IOL dependent: type, material, position
• surgeon dependent: technique of incision, placement of incision
• K (keratometry) and AL (axial length) measurement adjustments
• It approximately varies with a ratio of 1:1 with the IOL power.

27. Changing from one IOL design to Another
• The difference in A-constant between the two IOL types is the
same as the adjustment needed to the IOL power.
• For example, IOL power +20 D and A-constant of 119.2 in the
capsular bag, but switch with A-constant 118.7 in the capsular bag, we
need to drop the IOL power by 0.5 D to +19.5 D
• The difference of A-constants (119.2 – 118.7 = 0.5) is the same as the
difference in the IOL powers (20.0 – 19.5 = 0.5).

28. • Choosing the AC IOL power
• The original IOL for in-the-bag placement of power of +20 D with an
A-constant of 119.2
• but we have to implant an AC IOL with an A-constant of 115.7
• we need to drop the anterior chamber IOL power to +16.5 to have the
same refractive result.
• This drop from +20 to +16.5 is 3.5 D, which is the same as the
difference in A-constants (119.2 -115.7).

29. • Sulcus IOL placement-
• The sulcus IOL will need to have a power lower than the same IOL
placed in the capsular bag.
• This “Rule of 9s” says that IOL powers can be grouped into groups,
split at IOL powers 9, 18 and 27.
• The IOL power is reduced by 0.5 D, 1 D, and 1.5 D.

31. EFFECTIVE LENS POSITION
• Coined by Dr. Jack Holladay
• The position of the lens in the eye- specifically the distance that the
principal plane of the IOL will sit behind the cornea.
• The strength and predictability of the various IOL formulae depends
upon their ability to accurately predict the ELP
• “One of the most important and challenging tasks in IOL power
calculation is to predict the ELP for a given eye,” - Dr. Haigis

32. FACTORS INFLUCENING ELP
• Anatomical factors- Axial length
steepness of the cornea (average K)
limbal white to white measurements
preoperative anterior chamber depth
lens thickness
• 1st and 2nd generation IOL formulae tried to predict the ELP based
on anatomical factors alone.
• IOL and surgery related factors- The shape, the length, the flexibility,
the anterior angulation if any and the material of the haptic of the
IOL will affect the ELP.
• Individual Surgeon’s Technique
• Bag to sulcus shift- Requires reduction of 0.50-0.75 D from base
power of IOL.

34. • The difference is the manner in which Estimated lens
position(ELP) / Estimated post operative anterior chamber
depth(ACD) is calculated-
• Original formulas – ELP is a constant value
• Modified formulas – varies with axial length ( decreases in
shorter eye and increases in longer eyes)
• Modern formulas- ELP varies with axial length as well as
corneal curvature

35. • The ELP appeared with different names in different formulae
• SRKT- A Constant
• Holladay 2- S factor
• Haigis – a0, a1, a2
• Hoffer Q- pACD

36. • Various generations are grouped as-
A. First generation formulae -SRK 1 and BINKHORST
formula
B. Second generation formulae- SRK 2, Hoffer
C. Third generation formulae- SRK T, Holladay 1 ,
hoffer Q
D. Fourth generation formulae- Holladay 2, Haigis
E. Fifth generation formulae – Hoffer H 5

37. A. First generation formulae-
• These formulae based on three variables-
a) The AL of eyeball
b) K-reading and,
c) The estimated postoperative ACD
BINKHORST FORMULA ( Theoretical formulae) -
P= 1336 (4r-a)
(a-d)(4r-d)
Where, P is the IOL power in diopters
R is corneal radius in millimetres , a is AL in millimetres ,
d is postoperative ACD plus corneal thickness.

38. FIRST GENERATION FORMULA
SRK 1

39. • It was introduced by Sanders, Retzlaff and kraff (SRK) in 1980
• The postoperative ACD is not included but was replaced with A
constant which is unique to each different type of IOL.
• Suitable to use on axial length range- 22mm-24.5mm
• Erratic outside this range

40. RECOMMENDED FORMULA USAGE
• The main feature of the 1ST generation theoretical formula was –
Position of IOL in the eye is fixed for each lens type
• This assumption was true that time when cataract surgery was
represented by ICCE and ACIOL implantation.

41. DRAWBACKS OF FIRST GENERATION-
• They tend to predict too large an emmetropic value in short eyes less
than 22mm and too small values in long eyes more than 24.5mm.
• They are too cumbersome to apply without the use of calculator.
• Require a guess about the ACD, ultimate results depends on the
accuracy of the guess.

42. SECOND GENERATION FORMULA
SRK 2

43. • SRK 2 FORMULA - The basic equation of the formula is same i.e,
P= A1-2.5 L-0.9K , But the A constant is modified on the basis of AL
as
follows-
IF L is <20 mm : A+ 3.0
IF L is 20.00-20.99: A+2.0
IF L is 21.00-21.99: A+1.0
IF L is 22.0-24.5: A
IF L is >24.5 A-0.5

45. • MODIFIED SRK- 𝛱 FORMULA – In this formula, based on the AL , A
constant is modified as given:
IF L is <20 mm : A+ 1.5
IF L is 20-21mm: A+1.0
IF L is 21-22mm: A+0.5
IF L is 22.0-24.5mm: A
IF L is >24.5-26.0mm: A-1.0
IF L is >26mm: A-1.5

46. RECOMMEMDED FORMULA USAGE
• 2nd generation theoretical IOL formula differ from 1st generation
because- Position of IOL in pseudophakic eye is not fixed but
changes based on 2 variables : Axial length and corneal curvature or
corneal power of eye

47. •3rd GENERATION FORMULAE
•HOFFER Q, SRK/T, HOLLADAY 1

49. SRK/T FORMULA

50. • SRK/T – T for theoretical
• Third generation formula, described in 1990 by John Retzlaff
and Donald Sanders.
• Benefits of both the theoretical and regression formulae
• Theoretical element- predicted post op ACD, Retinal
thickness adjusted axial length, refractive indices of cornea
• Regression element- optimise A Constant
• Useful in Normal length and moderately long and very long
eyes(> 26mm)

52. • The SRK T formula has made the SRK 2 formula obsolete
since it combines all the advantages of the SRK 2 formula
and also enables you to optimize the A-Constant
• What is optimization - optimization is achieved by analyzing
post operative outcomes with respect to the targeted
refraction for a given surgical technique and a specified
model or design of IOL as well as for a given range of axial
lengths
• This optimization is then added on to the ‘A constant’ to
make the formula more predictable.

53. HOFFER Q

54. • Third generation formula
• Was described by Dr. Kenneth Hoffer in 1993
• P = f (A, K,Rx, pACD)
A: axial length
K: average corneal refractive power (K-reading)
Rx: Previous refraction
pACD personalized ACD (ACD-constant)
• Hoffer –Q formula was such that it was extremely reliable in
short eye balls with an axial length of less than 22.0mms

55. • Uses personalised post operative ACD as A constant
• Used for AXL < 22.00 mm . Accurate prediction with Hoffer Q when
compared with SRK T and Holladay 1
Hoffer KJ. The Hoffer Q formula: a comparison of theoretic and regression formulas. J
Cataract Refract Surg. 1993;19:700–712.

56. FORMULA REQUIREMENTS

57. • In medium AL range, 3rd generation formulas are equally accurate
• In an analysis of >13,000 surgeries, all formulas, including the third
generations, had prediction errors within 0.1D of the predicted
refraction when used for medium length eyes (AL 23 – 25 mm).*
• Moving outside of this range, the prediction errors increase widely
among the formulas.
• Few other studies demonstrate similar overall mean absolute error for
SRK/T, Holladay 1, and Hoffer Q, with a slightly lower absolute error
for Holladay 1.**
*Melles RB, Holladay JT, Chang WJ. Accuracy of intraocular lens calculation formulas. Ophthalmology. 2018;125:169–178.
**Darcy K, Gunn D, Tavassoli S, Sparrow J, Kane JX. Assessment of the accuracy of new and updated intraocular lens power calculation formulas in 10 930 eyes from
the UK National Health Service. J Cataract Refract Surg. 2020;46:2–7.

58. WHEN TO USE HOFFER Q?
• Hyperopes (AL < 22 mm)
• Most accurate in short eyes < 20.0mm, confirmed in large study of
830 short eyes
• Had the lowest mean absolute error (MAE) for AL 20.0mm to
20.99mm
• Hoffer Q and Holladay 1 had lower MAE than SRK/T for AL 21.0mm
to 21.49mm
• In post corneal refractive surgery

59. HOLLADAY 1

60. • 3rd generation formula
• Produced by Jack Holladay in 1988
• Require only 2 variables: AXL and K for IOL power calculation
but also requires optimisation of equation for more accurate
prediction of ELP
• Work best for eyes between 24.5-26mm(medium long eyes)

61. • ACD = CT + (CORNEAL ENDO + iris plane) + ( iris + IOL position)
• Iris plane + IOL position = surgeon factor (this is known post
operative only) hence , varies with lens type and requires optimisation
• SURGEON FACTOR- Distance between iris plane and IOL optic plane .
A change of 1mm of post operative AC depth causes 1.5 D change in
final refraction.

62. • SURGEON FACTOR (SF)
• Distance between iris plane & IOL optic plane
• SF should be personalized
• " A change in the true post-operative AC depth will affect the
refractive status of the eye.
• SF constants must be personalized to accommodate any consistent
shift that might affect IOL power calculation

64. FOURTH GENERATION FORMULAE
HAIGIS,OLSEN , HOLLADAY 2

65. HAIGIS

66. • 4th generation formula
• A/k/s GOW70
• The versatility of the formula lies in the three individualized A
constants namely a0, a1 and a2
• The a0 is linked to the manufacturers lens constant
• The a1 is linked to the pre operative ultrasonically measured
anterior chamber depth (this has a default value of 0.4)
• a2 which is linked to the axial length measurements and which
has a default value of 0.1

67. • 3 a constants : can customise each component of IOL
• Work well across entire range of axial length

68. • The Melles et al’s analysis - Haigis formula demonstrated
low variability in prediction error across the range of AL
(21–28 mm) and ACD (2.25–4.25 mm) analyzed, suggesting
that the Haigis formula may be good for a wide range of
eyes*
*Melles RB, Holladay JT, Chang WJ. Accuracy of intraocular lens calculation
formulas. Ophthalmology. 2018;125:169–178.

69. The three ‘A constants’ enable
to customize each component
of the IOL formula.
When fully optimized this
formula will work across the
entire range of axial length
values and you may not need
to use different formulae for
different axial lengths.

70. HOLLADAY 2

71. • 4th Generation Formula
• Dr Jack T Holladay has attempted to increase its accuracy and
predictability by incorporating seven different parameters into
the formula which contribute accurate estimation of the ELP.
• Axial length
• Central corneal power (K)
• Anterior chamber depth
• Lens thickness measurement
• Limbal white to white measurement
• Age of the patient
• Previous refraction of the patient

72. • The ‘nine types’ of eyes model by Dr. Holladay
• The assumption that there was a constant relationship between the
central corneal power (K), the pre operative anterior chamber
depth and the axial length measurement.

73. No direct
correlation
between the axial
length
measurements
and the anterior
chamber size.
This model
overcame the
discrepancies in
all the other IOL
formulae

74. • It is available as part of a package called the ‘Holladay IOL consultant’
which also provides the necessary information to optimize every
component of the surgeon factor(SF).

75. T2 formula
• In SRK T formula a corrected Axial length is used in calculations
• This corrected axial length used to calculate imaginary ACD – source
of error
• In T2 formula, corrected AXL is not used.
• T2 Formula is better than SRK /T for AXL 24.5 to 26 mm
• Although T2 Improved on SRK /T , it still has limitations of being
based on 2 variables
Kane JX, Van Heerden A, Atik A, Petsoglou C. Intraocular lens power formula accuracy: comparison of 7 formulas. J Cataract
Refract Surg. 2016;42:1490 – 1500.

76. OLSEN

77. OLSEN FORMULA
Olsen formula uses both
marginal and paraxial ray
tracings of optical light through
the refractive media in the eye,
including the specific optics of a
particular IOL, to derive the
postoperative position of that
lens.

78. • More precise and specific than theoretical formulas
• Fewer number of surgical cases are needed to validate or
optimize the C constant
• Study comparing the Olsen ray tracing formula with Haigis,
Hoffer Q formulas showed no significant improvement with
the Olsen*
*Jin H, Rabsilber T, Ehmer A, et al. Comparison of ray-tracing method and
thin-lens formula in intraocular lens power calculations. J Cataract Refract
Surg. 2009;35:650–662.

79. BARRET UNIVERSAL II

80. • Universal – highly accurate over wide range of axial lengths
and different type of IOL materials
• Vergence formula (Theoretical and regression model)
• Theoretical model of the eye in which the anterior chamber
depth (ACD) is related to the AL and corneal curvature (K)
• Regression model of the eye predicts the distance from the
iris root to the second principal plane of the lens denoted by
an individualized lens constant known as the lens factor.

81. The Lens Factor, is the
distance from the Iris
plane to the second
principal plane of the
IOL
A relationship between
the A-constant and a "lens
factor" is also used to
determine ACD.

83. • The important difference between the Barrett formula and
other formulas is that the location of the Secondary principle
plane of refraction of the IOL is retained as a relevant
variable in the formula so its UNIVERSAL

84. • Parameters used for ELP prediction
• The effective lens position (ELP) is calculated with the help
of ACD and a lens factor (LF), which itself is dependent on
five variables:
• Keratometry (K), Axial length (AL), Anterior chamber
depth(ACD), lens thickness (LT), and Horizontal white-to-
white (W-W)
• Recommended eye type
• The Barrett formula is recommended for short – long eyes

85. • The formula can be accessed in the online form in Asia Pacific
Association of Cataract and Refractive Surgeons website.
• https://www.apacrs.org/barrett_universal2/

87. • Retains positive correlation of AXL and K values and ACD
• Accuracy is because of : incorporation of principle plane of the IOL
formula
• Most accurate when compared with Other 3rd and 4th gen formulae*
*Cooke DL, Cooke TL. Comparison of 9 intraocular lens power calculation formulas. J Cataract Refract Surg. 2016;42:1157–1164.

88. • Barrett universal 2 is accurate across wide range of AL and ACD
compared to earlier formulae.*
• Least refractive surprise when compared to other earlier formulae
Xia, T., Martinez, C.E. and Tsai, L.M. (2020) “Update on intraocular lens formulas and calculations,” Asia-Pacific Journal of Ophthalmology, 9(3), pp. 186–193.
Available at: https://doi.org/10.1097/apo.0000000000000293.

89. HILL RBF

90. • Pattern recognition of AI accounts for the errors caused due
to “undefined factors”
• Limitation : as it is based on database , type of data and eye
characteristics from which it is derived
• Algorithm continuously evolves as increasing data is fed
• Hill-RBF 2.0 (2018) has been released, which is derived
from a larger data-set with expanded “in-
bounds” biometry ranges

91. • RBF- Radial Basis Function
• Came in 2016, which was the first formula based on artificial
intelligence (AI)
• It is pure data based IOL Calculation approach and therefore
it is free of the limitation of the effective lens position.
• Artificial intelligence + regression analysis
• It can be used for all IOL from -5 D to +30D independent of
eyes anatomy ( short/ medium/ large)

92. Darcy K, Gunn D, Tavassoli S, Sparrow J, Kane JX. Assessment of
the accuracy of new and updated intraocular lens power
calculation formulas in 10 930 eyes from the UK National
Health Service. J Cataract Refract Surg. 2020;46:2–7.
• Barrett universal 2 :
• larger overall mean error compared with
Olsen
Hill RBF
• Comparable with AL adjusted holladay 2
• When analysed with different categories of AL ,
• Barrett had less error with long AXL ( >26.0mm)
• And equivalent to Olsen in medium eyes ( 22.0 -
26.0mm)

93. • Kane formula
• Artificial intelligence with theoretical optics of IOL power
prediction
• Required parameters : AL , corneal power, ACD, gender,
and A constant
• In the 2020 study of 10,930 eyes, the Kane formula was
the most accurate formula for all ranges of ALs, with the
smallest absolute error for long eyes, AL >26.0 mm.*
*Darcy K, Gunn D, Tavassoli S, Sparrow J, Kane JX. Assessment of the accuracy of new
and updated intraocular lens power calculation formulas in 10930 eyes from the UK
National Health Service. J Cataract Refract Surg. 2020;46:2–7.

94. • Ladas formula:
• Works by combining most accurate portions of IOL
formulae to make “super formula”
• Depending on AL and k values , it will choose among
available formula and combine these
• SRK T, Hoffer Q, Holladay 1 , Holladay with Wang Koch
adjustment, Haigis

95. Wang Koch adjustment
• A Wang-Koch (WK) adjustment can be applied to some
third- and fourth-generation IOL formulas to optimize the
calculation for AL >25 mm
• Holladay 2 formula can be improved by this adjustment*
• Results of such optimised Holladay 2 formulae was
comparable with Barrett universal 2 and better than Holladay
1*
Darcy K, Gunn D, Tavassoli S, Sparrow J, Kane JX. Assessment of the accuracy of
new and updated intraocular lens power calculation formulas in 10 930 eyes
from the UK National Health Service. J Cataract Refract Surg. 2020;46:2–7.

96. • WK adjustment shift refractive outcomes in long eyes from
hyperopic to myopic
• Can be considered as an adjunct to the use of the Holladay 1,
Hoffer Q, SRK/T, and Haigis formulas in long eyes
Adjusted axial length = 0.8453 ×
measured axial length + 4.0773 mm

97. • INTRA OPERATIVE ABERROMETRY ORA SYSTEM
• WaveTec Vision Intraoperative Wavefront Aberrometry-
ORA System
• Optiwave refractive analysis
• To allow to take both aphakic and pseudophakic refractive
measurements in the operating room

98. • Fits on bottom of surgical microscope
• Improves accuracy in IOL Power calculations including post
refractive surgery patients
• More precise in Toric IOL placement
• Consistency in LRI procedures

99. Summary

100. FORMULA YEAR FORMULA
CLASSIFICATION
VARIABLES ADVANTAGES DISADVANTAGES
SRK/T
1990 Vergence
•AL
•K
•A-constant
•Post-
operative
refractive
target
• Accurate in eyes
with normal axial
lengths and mean
keratometry values
• Accurate in axial
myopes compared to
holladay 1 and 2
hoffer Q
• Wang-Koch
adjustment can be
easily applied to
further enhance
outcomes in axial
myopes
Pre-installed on:
• AL-Scan (Nidek)
• Aladdin (Topcon)
• Anterion
• EQ Workplace
(Zeiss)
• Galilei G6 (Zeimer)
• IOLMaster 700
(Zeiss)
• OA-2000 (Tomey)
• Less accurate in
long eyes than
modern vergence-
based formulas (
BU-II, EVO, Hill-
RBF, Kane)
• Assumes normal
ACD

101. FORMULA YEAR FORMULA
CLASSIFICATION
VARIABLES ADVANTAGES DISADVANTAGES
Hoffer Q 1993 Vergence • AL
• K
• pACD
• Post-
operative
refractive
target
• Accurate in short eyes
Pre-installed on:
• AL-Scan (Nidek)
• Anterion (Heidelberg
Engineering)
• EQ Workplace (Zeiss)
• Galilei G6 (Zeimer)
• IOLMaster 700 (Zeiss)
• OA-2000 (Tomey)
• Veracity Surgery
Planner (Zeiss)
• Vision Planner
(Alcon)
• No use of
anatomic
ACD, so
theoretically
less reliable
in
anatomically
abnormal
anterior
segments
• Recommende
d to be
replaced by
Hoffer QST

102. FORMULA YEAR FORMULA
CLASSIFICATI
ON
VARIABLES ADVANTAGES DISADVANTAGES
Holladay 1
1988 Vergence
•AL
•K
•SF
•Post-
operative
refractive
target
• Accurate for short eyes
Unique relationships of AL and K
adjust for anterior segments
accurately
Pre-installed on:
• AL-Scan (Nidek)
• Aladdin (Topcon)
• Anterion
• EQ Workplace (Zeiss)
• Galilei G6 (Zeimer)
• IOLMaster 700 (Zeiss)
• OA-2000 (Tomey)
Less accurate in long eyes
(hyperopic results)
Holladay 2
1995 Vergence
•AL
•K
•ACD
•LT
•WTW
•CCT
•Age
•A-
constant/A
CD/SF
•Post-
operative
refractive
target
• Open Access Calculator
Button on website permits
Forward and Back
Calculation of Holladay 2
Formula
• Along with BU, accurate in
pediatric populations
Pre-installed on:
• EQ Workplace (Zeiss)
• IOLMaster 700 (Zeiss)
• Veracity Surgery Planner
(Zeiss)
• Vision Planner (Alcon)
Less accurate in long
eyes(hyperopic results)

103. FORMULA YEAR FORMULA
CLASSIFICATI
ON
VARIABLES ADVANTAGES DISADVANTAGES
Haigis 2004
Vergence
• AL
• K
• ACD
• 3 constants:
a0
A1(measured
ACD)
A2(measured
AL)
• Post operative
refractive target
• Accurate in short
eyes (AL<22mm)
• Accurate for stage
III keratoconus
eyes
• Pre-installed on:
• Aladdin (Topcon)
• Anterion
(Heidelberg
Engineering)
• EQ Workplace
(Zeiss)
• Galilei G6 (Zeimer)
• IOLMaster 700
(Zeiss)
• OA-2000 (Tomey)
• Less accurate in
long eyes
• Resulting
hyperopic
outcomes in long
eyes using Haigis
alone, which can
be addressed using
Haigis with Wang-
Koch adjustment
• Less accurate in
eyes with extreme
LT values

104. FORMULA YEAR FORMU
LA
CLASSIFI
CATION
VARIABLES ADVANTAGES DISADVANTAGES
Barrett
Universal
(BU)
Version
I: 199
Version
II:
2010
Vergen
ce
• AL
• K
• ACD
• LT
(optional
)
• WTW
(optional
)
• LF/DF
or A-
constant
• Post-
operativ
e
refractiv
e target
• Accurate in long eyes
• Accurate in normal
ranges AL
• Along with Holliday 2,
accurate in pediatric
populations
• Best in eyes with mild-
moderate keratoconus
• Easily accessible for free
online
• Pre-installed on:
• AL-Scan (Nidek)
• Aladdin (Topcon)
• Anterion (Heidelberg
Engineering)
• EQ Workplace (Zeiss)
• IOLMaster 700 (Zeiss)
• OA-2000 (Tomey)
• Veracity Surgery Planner
(Zeiss)
• May be less accurate in
short eyes (i.e. AL
≤22.0mm
• However, BU-II can still
provide excellent
refractive outcomes with
AL <22.5mm or AL
20.8mm-22.0mm

105. FORMULA YEAR FORMULA
CLASSIFICATION
VARIABLES ADVANTAGES DISADVANTAGES
Hill-RBF
Version
2: 2018
Version
3: 2020
Artificial
Intelligence
• AL
• K
• ACD
• LT (optional)
• WTW
(optional)
• CCT (optional)
• A-constant
• Post-operative
refractive
target
• Prediction
accuracy
continues to
improve as
more data is
analysed
• May
outperform
BU-II
• Haigis and Hill-
RBF V.2.0 were
significantly
influenced by LT,
independently of
the ACD
• myopic shift with
thin lenses and a
hyperopic shift
with thick lenses

106. FORMULA YEAR FORMULA
CLASSIFICATION
VARIABLES ADVANTAGES DISADVANTAGES
Kane
2017
Blended (Vergence,
Regression, and
Artificial Intelligence-
based)
•AL
•K
•ACD
•LT (optional)
•CCT (optional)
•Gender
•A constant
(developed to be
similar to
SRK/T A-
constant)
•Post-operative
refractive target
• Accurate in short
eyes
• Accurate in long
eyes ( AL ≥26mm)
• Prediction accuracy
continues to
improve as more
data is analysed
• Accurate in
extreme ACD (
≤3.0mm)
• Easily accessible
for free online
Pre-installed on:
• Veracity Surgery
Planner (Zeiss)
• EQ Workplace
(Zeiss)
Ladas Super
formula 2015 Artificial Intelligence
• most ideal
calculations
from other
formulas
(SRK/T, Hoffer
Q, Holladay 1,
Holladay with
WK adjustment,
Haigis
•Post-operative
refractive target
• Prediction accuracy
continues to
improve as more
data is analysed
• Newer versions
including Toric and
Post-LASIK
calculators

107. Optimisation of IOL formula
• Making a formula more predictable by refining manufacturers lens
constant
• Optimisation achieved by : analysis of post operative outcome with
respect to target refraction ( for a specific surgeon, specific IOL and
given range of Axial length)
• This optimisation is then added to A constant to make it more specific

108. • Why to optimise
• Most IOL formulae accurate for AXL 22 – 26 mm
• Outside this range : inaccuracy increases
• This is because
• A constant is computed based on AVERAGE axial length
of 23.50 mm
• Formulae ASSUME direct proportional relationship
between AXL and Post op ACD and corneal steepness.

109. HOW TO OPTIMISE (FOR SRK/T)
• Minimum of 25 eyes
• Same surgical technique to be used
• A scan and k values by same person
• Post operative 6 weeks results to be analysed: to look for difference
between target refraction and actual post op result
• Enter data in electronic spreadsheet: https://doctor-hill.com/
• Optimised A constant then can be downloaded
• Optimisation for specific axial length range :
• Short eyes 20 - 22.0 mm
• Normal: 22 – 24.5 mm
• Long eyes 24.5mm – 26.00

111. • But 4th gen IOL formulae can be optimised over the entire
range of AXL.
• Haigis formula has constants linked to manufacturers lens
constant, POST OP ACD, AXL
• 4th generation formulae require 200 cases or more for
optimization of IOL power
• website: www.augenklinik.uni-wuerzburg.de/ulib

112. SPECIAL SITUATIONS

113. APHAKIC EYES-
• Speed of travel of sound is altered (1532m/s) – Slower speed than
phakic eyes(1550m/s).
• Two lens spikes in A-scan are Replaced by a single spike of the
anterior vitreous face and posterior lens capsule
• Immersion method is preferred
• Optical biometers with aphakic mode
• Depending on type of IOL deductions should be done.

114. VELOCITY CONVERSION EQUATION
• correct measurement when an inappropriate sound velocity is used during
the examination correct value = (Vc/Vm) X measurement
• The formulae are as follows:
• 1IOL power (D) = Aphakic refraction x 2.01
• 2IOL power (D) = Aphakic refraction x 1.75
• 3IOL power (D) = 0.07x(2) + 1.27x + 1.22, where x = aphakic refraction
1) Ianchulev et al., J. Cataract Refract. Surg. 31 (2005) 1530
2) Mackool et al., J. Cataract Refract. Surg.32 (2006) 435
3) Leccisotti, Graefes Arch. Clin. Exp. Ophthalmol.246 (2008) 729

115. • All the formulae (Holladay 1, Hoffer Q, SRK/T, and SRK II)
showed hyperopic shift, SRK/T showed the best accuracy
• Biometry-based formulae (Holladay 1, Hoffer Q, SRK/T, and
SRK II) formulae were superior to Ahakic Refraction-based
formulae in accuracy of IOL power calculation when IOL
was implanted in the sulcus or in the bag

116. PSEUDOPHAKIC EYES
• Required in - unexpected
postoperative refractive surprise,
IOL Exchange, for comparison
while doing biometry for other
eye.
• correct setting on the machine
• measurement performed in the
phakic or cataract mode will
produce erroneous results
• Reducing gain to decrease the
artificial spikes and make retinal
ones more prominent.

117. • Manual mode is preferred
• Best way to record axial length in the pseudophakic eye is to use an
optical biometer
• Optical Biometry is preferred which offers more accurate correction
of the AL by correction factor (CF) which varies as per the lens type
and thickness.

118. • In biphakic eye (pseudophakia with phakic IOL) -Thickness (T) and
material specific correction factor (C) of the implanted phakic IOL

119. • Apparent Axial Length(AAL) – AL measured in pseudophakic eye
with sound velocity of 1550m/s which is standard setting for
cataractous eye

120. • SECONDARY PIGGYBACK IOL FOR PSEUDOPHAKIA
• It is often easier to surgically implant secondary piggyback IOL and
leave primary IOL in place to achieve desired refraction.
• Gill’s nomogram for residual hyperopia and residual myopia-

121. PIGGY-BACK IOLS
• Post IOL refractive surprise or in those with large dioptric
requirement, a piggy back IOL in sulcus can be placed along with the
primary implant.
• Myopic correction: P = 1.0 x Error
• Hyperopic correction: P = 1.5 x Error
Where P = the needed power in the piggyback lens Error = the residual
refractive error that needs to be corrected
Findl O , Menapace R. Piggyback intraocular lenses [letter].JCataract Refract SLlrg. 2000;26(3): 308~30 9.
Findl O , Menapace R, Rainer G, Georgopoulos M. Contact zone of piggyback acryliCintraocular lenses. , Cataract
Refract Surg. 1999;25(6):860- 862

122. SHORT AND LONG EYES
• Haigis, Hoffer Q, and Holladay 2 formulas are the best for intraocular
lens power prediction in short eyes (<22 mm).
• In long eyes (>26 mm), the Barrett Universal II, Haigis (with
optimized constants), Olsen, and SRK/T formulas provide the most
accurate outcomes.

123. • Greater accuracy - Hoffer Q formula in eyes shorter than 22 mm
• Holladay 2 was equally as accurate as the Hoffer Q in eyes shorter
than 22 mm, and that it was less accurate than the Holladay 1 in eyes
between 22 and 26 mm

126. SILICONE FILLED EYE
• Low sound velocity (987m/s) and difficulty in identifying retinal
spike
• Error in Axial length measurements occur as ultrasound travels longer
time to reach the probe which is interpreted as longer measurements-
post operative hyperopic results
• Optical biometer with silicone oil mode is preferred
• Usually IOL required is 2-3 D stronger than indicated by standard
power calculation

127. • True vitreous length =980/1532x Apparent Vitreous Length
• Corrected axial length=True vitreous length+ ACD+ Lens thickness
• Corrected Axial Length= Correction factor(0.71) x measured AL

128. • True axial length (AL) of the silicone oil-filled (viscosity 1300
centistokes) eye can be estimated from the measured AL (MAL)
obtained on A and/or B scan echography, by multiplying MAL by a
conversion factor of 0.71.
• IOL power can then be calculated using current biometry formulae
(SRK/T).

129. POSTERIOR STAPHYLOMA
• Myopic eyes poses a challenge
because of the localization of the fovea
• The best method of ensuring that the
optical path length is measured is to
use optical biometry

130. • B Scan can be used to demonstrate shape of posterior ocular wall and
relationship of macula to the staphyloma
• Probes with fixation lights are preferable
• Optical biometer preferred
• Barret universal II formula preferred
• Optimised axial length/or optimized IOL constants minimizes error

131. CORNEAL ECTASIA
• Patients with corneal ectasias, such as keratoconus, pellucid marginal
degeneration and post-refractive ectasia
• Irregular astigmatism
• disease progression
• Among devices- The reproducibility is best with the Pentacam
because it incorporates posterior corneal curvature compared to
optical biometry.
• The Pentacam also tends to measure flatter keratometry values when
compared with optical biometry and avoid hyperopic outcomes.

132. • K Values- Prefer to utilize standardized K value (43.25D) or utilize
the Barrett formula and aim at least 3 dioptres more myopic than the
actual targeted refractive outcome*
• IOL Formulae- SRK/T was found to have the smallest absolute error
when compared with other formulas such as SRK II, Haigis, HofferQ,
and Barrett Universal II**
*Watson MP, Anand S, Bhogal M, et al. Cataract surgery outcome in eyes with keratoconus. Br J
Ophthalmol. 2014;98:361–364.
**Savini G, Abbate R, Hoffer KJ, et al. Intraocular lens power calculation in
eyes with keratoconus. J Cataract Refract Surg. 2019;45:576–581.

133. • Wang et al with 73 eyes compared SRK/T, Hoffer Q, Holladay I and
II, Haigis and Barrett Universal II and demonstrated that for mild and
moderate keratoconus- Barrett Universal II had the smallest
prediction error.
• For severe keratoconus, all formulas performed poorly but Haigis had
the smallest error.
Wang KM, Jun AS, Ladas JG, Siddiqui AA, Woreta F, Srikumaran D. Accuracy of intraocular lens
formulas in eyes with keratoconus. Am J Ophthalmol. 2020;212:26–33.(MOST RECENT STUDY)

134. • No studies on the newer artificial intelligence-based algorithms to
corneal ectasias

135. POST REFRACTIVE SURGERY EYES
Refractive surgery alters
the corneal curvature and
introduces error into both
the measurement of
corneal power and the
prediction of ELP
underestimation of IOL
power in eyes with myopic
refractive surgery and an
overestimation IOL power in
eyes with previous
hyperopic refractive surgery.

136. Laser vision
correction(LASIK/SMILE/LASE
K or PRK), the
anterior surface is affected while
the posterior surface remains
unaltered
So ratio changes
Radial keratotomy flattens
both the anterior and
posterior corneal surfaces,
but only in a small central
optical zone

137. • Errors in ELP Estimation
• Third-generation formulae link the ELP estimation to the
keratometry reading
• Myopia – flattening of cornea without changing anterior
chamber depth
• False low estimate of ELP, with the formulae predicting a
more anteriorly placed IOL
• Reversed occurs in hyperopic eyes

139. • CLINICAL HISTORY METHOD-
• Refractive status prior to the refractive surgery and the post-correction
refractive status
• The corneal power is calculated by subtracting the change in manifest
refraction at the corneal plane induced by the refractive surgical
procedure from the corneal power values obtained before refractive
surgery.

140. • Clinical history method is not suitable for RK because of unstable
corneal power (Post RK cornea typically flattens progressively over
many years)

141. • CONTACT LENS OVER-REFRACTION METHOD
• Corneal power is calculated as the sum of the contact lens base curve,
power, and over-refraction minus the spherical equivalent of the
manifest refraction without a contact lens.
• Suitable for both post LASIK and RK corneas

142. • TOPOGRAPHY-BASED POST-LASIK ADJUSTED
KERATOMETRY
• Based on analysis of post-LASIK corneal topography central Ks (TK)
in LASIK eyes.
• True corneal power is predicted using only the single central
postoperative reading TK.
• They are based on LASIK data and are not suitable for post-RK cases.

143. *Koch, D. and L. Wang, Calculating IOL power in eyes that have had refractive surgery. J
Cataract Refract Surg, 2003. 29: p. 2039 - 2042.
*Shammas, H.J., et al., Correcting the corneal power measurements for intraocular lens
power calculations after myopic laser in situ keratomileusis. Am J Ophthalmol, 2003.
136(3): p. 426-32

144. • CENTRAL RING TOPOGRAPHY METHOD
• Corneal refractive power after RK was best described by averaging
the topographic corneal power of the central 3.0 mm area.
• Applying this method, together with a double-K IOL formula,
achieved excellent IOL power predictability.
• Not suitable for LVC eyes

145. • NET CORNEAL POWER MEASUREMENT
• Solution to obtaining accurate corneal power is to directly measure
both anterior and posterior corneal curvature and thereby calculate the
net corneal power.
• Several instruments (orbscan 2 videokeratography , pentacam, optical
coherence tomography) can directly measurement of both anterior and
posterior corneal surfaces.

146. • IOL Power Formulae for Post-Refractive Surgery Eyes
• Double k formula
• Hoffer Q formula
• Haigis L formula
• Masket formula

148. • DOUBLE K FORMULA-
• In “double-K” version of IOL formula, the post-refractive surgery
corneal power reading is used in the vergence calculation while the
pre-refractive surgery corneal power (or an estimate) is used in the
ELP prediction formula.
• Double-K versions of SRK/T, Hoffer Q and Holladay II formulae are
available.
• The double-K Holladay II formula allows both a post-RK and a post-
LVC setting.

149. • HOFFER Q FORMULA
• ELP calculation is less sensitive to corneal power variation.
• So less error in post-refractive surgery eyes than other single-K
formulae
• If double-K formulae are not available, the single-K Hoffer-Q formula
may be useful
• HAIGIS-L FORMULA
• Built-in software of IOLMaster
• Corneal power is calculated by inputting IOL-Master biometry as
follows: axial length (AL), anterior chamber depth (ACD),
keratometry
• only suitable for post-LVC cases, not post-RK cases (based on LASIK
data)

150. • MASKET FORMULA
• They recommend using the SRK/T formula for myopic ALs and the
Hoffer Q for hyperopic ALs.

151. • KOCH AND WANG NOMOGRAM ADJUSTMENT
• Separate nomograms for both post myopic and hyperopic refractive
surgeries
• Easy to use by just look up the axial length of the patient and add or
subtract the adjusted IOL power to the IOL power calculated using the
SRK/T, Hoffer Q, and Holladay 1 formulas
• Choose higher IOL power or select lower corneal power estimation to
use in IOL calculation

152. IOL Calculators-
• ASCRS website (website based post-LVC and post-RK IOL
calculator): https://ascrs.org/tools
• Post-LVC IOL calculator: https://www.eyelab.com/
• IOLMaster reference: https://doctor-hill.com/iol-power-calculations/

153. POST KERATPLASTY PATIENTS-
• IOL implantation can be a part of TRIPLE PROCEDURE or in prior
grafted eyes.
• For triple procedure better keep aphakic , 4-8 months later can plan
secondary IOL provided all sutures removed.
• Biometry from fellow eye
• Central corneal power values input from topography
Indian J Ophthalmol. 2010 Mar-Apr; 58(2):115-8

154. • Optical biometer preferred
• 3th and 4th generation formulae suggested
• Toric IOLs can also preferred to correct high astigmatism provided
stable refraction after complete suture removal

155. PAEDIATRIC IOL POWER CALCULATION-
• Increased errors in AL measurement, which compounds the final IOL
power errors due to shorter AL.
• AL and K value must be measured under general anaesthesia.
• The IOL power chosen should allow good vision in growing age to
prevent amblyopia and ideally also give emmetropia in adult age.
• All infants above two years are advised IOL implantation

156. • RULE OF 7- Enyedi proposed “the rule of 7 ” where the sum of
postoperative refractive goal and age of the child is 7 and target
refraction is decided accordingly.
American Journal of Ophthalmology, Volume 174 - Feb 1, 2017

157. Khokhar SK, Tomar A, Pillay G, Agarwal E. Biometric changes in Indian pediatric
cataract and postoperative refractive status. Indian J Ophthalmol. 2019
Jul;67(7):1068-1072.

158. • INFANT APHAKIA TREATMENT STUDY
• Overall, SRK/T was found to give the minimum average prediction
error (0.3 D) and Hoffer Q the highest error (2.3 D)
• They concluded that that SRK/T and Holladay 1 yield good results in
infants less than 2 years or with AL ≤21 mm
• Whereas Barrett and Haigis formulas were better in patients older
than 2 or with AL >21 mm
Infant Aphakia Treatment Study Group; Lambert SR, Buckley EG, Drews-Botsch C, DuBois L, Hartmann E,
Lynn MJ, Plager DA, Wilson ME. The infant aphakia treatment study: design and clinical measures at
enrollment. Arch Ophthalmol. 2010 Jan;128(1):21-7

159. • Study of 20 Saudi paediatric patients included the Barrett Universal II
and Olsen formulas in its comparison with the formulas (SRK 2,
SRK/T Holladay 1 and Holladay 2 , Hoffer Q
• Both the Barrett and Olsen had larger prediction
• Error compared with all other formulas except for the Haigis
• SRK II was most accurate
An-Nakhli FR. Accuracy of new and standard intraocular lens power calculations
formulae in Saudi pediatric patients. Taiwan J Ophthalmol. 2019;9:37–42 (RECENT
STUDY)

160. Grouped as - short (%22.0 mm), medium(>22.0 to <24.5 mm), medium long (24.5 to
<26.0 mm), and long (>26.0 mm)
3241 patients , 5 years duration
Barrett Universal II formula had the lowest mean absolute prediction error over the
entire AL range
No statistically significant difference in the short AL subgroup
J Cataract Refract Surg 2016; 42:1490–1500 Q 2016 ASCRS and ESCRS

161. • Thank you