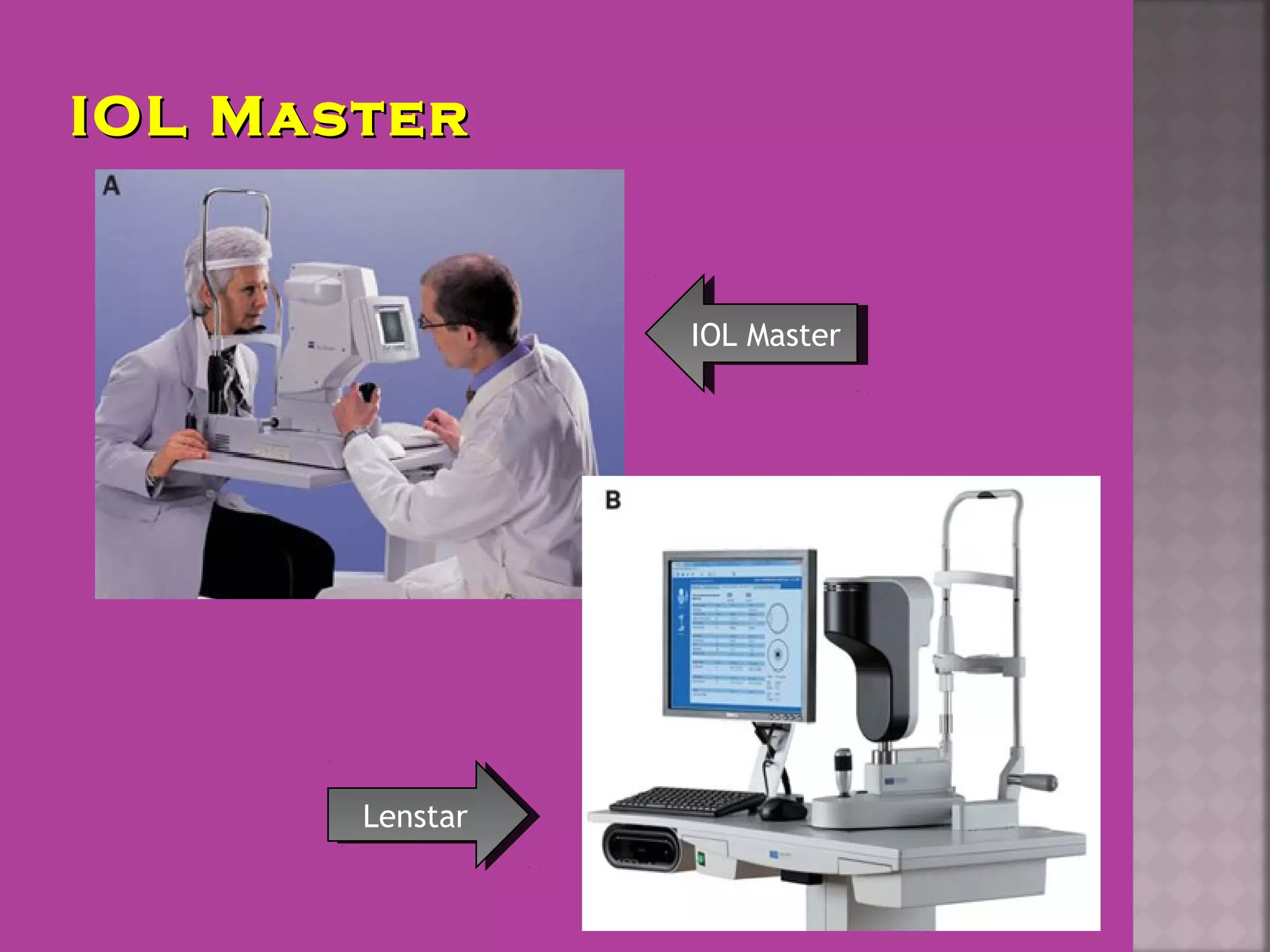
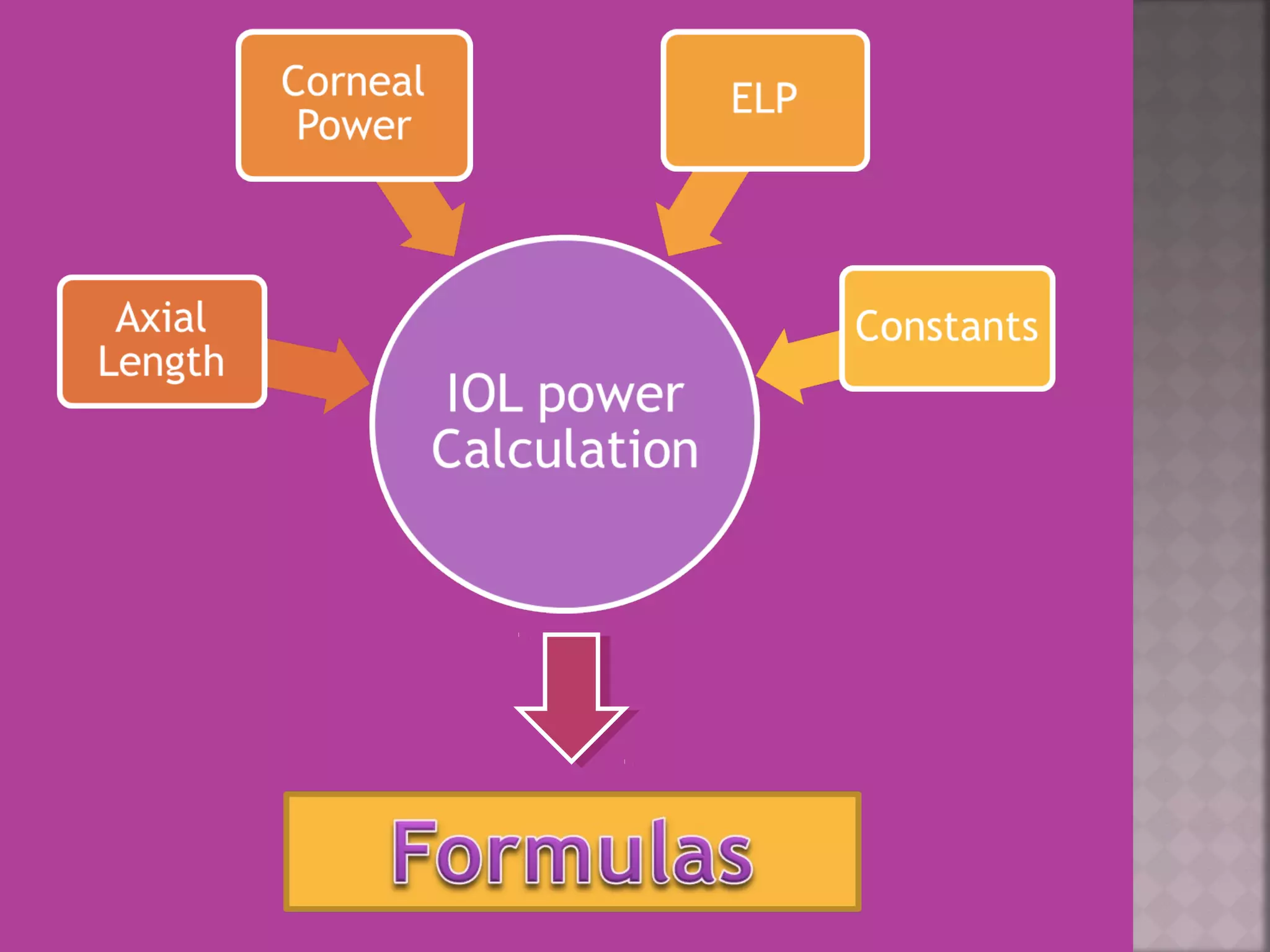
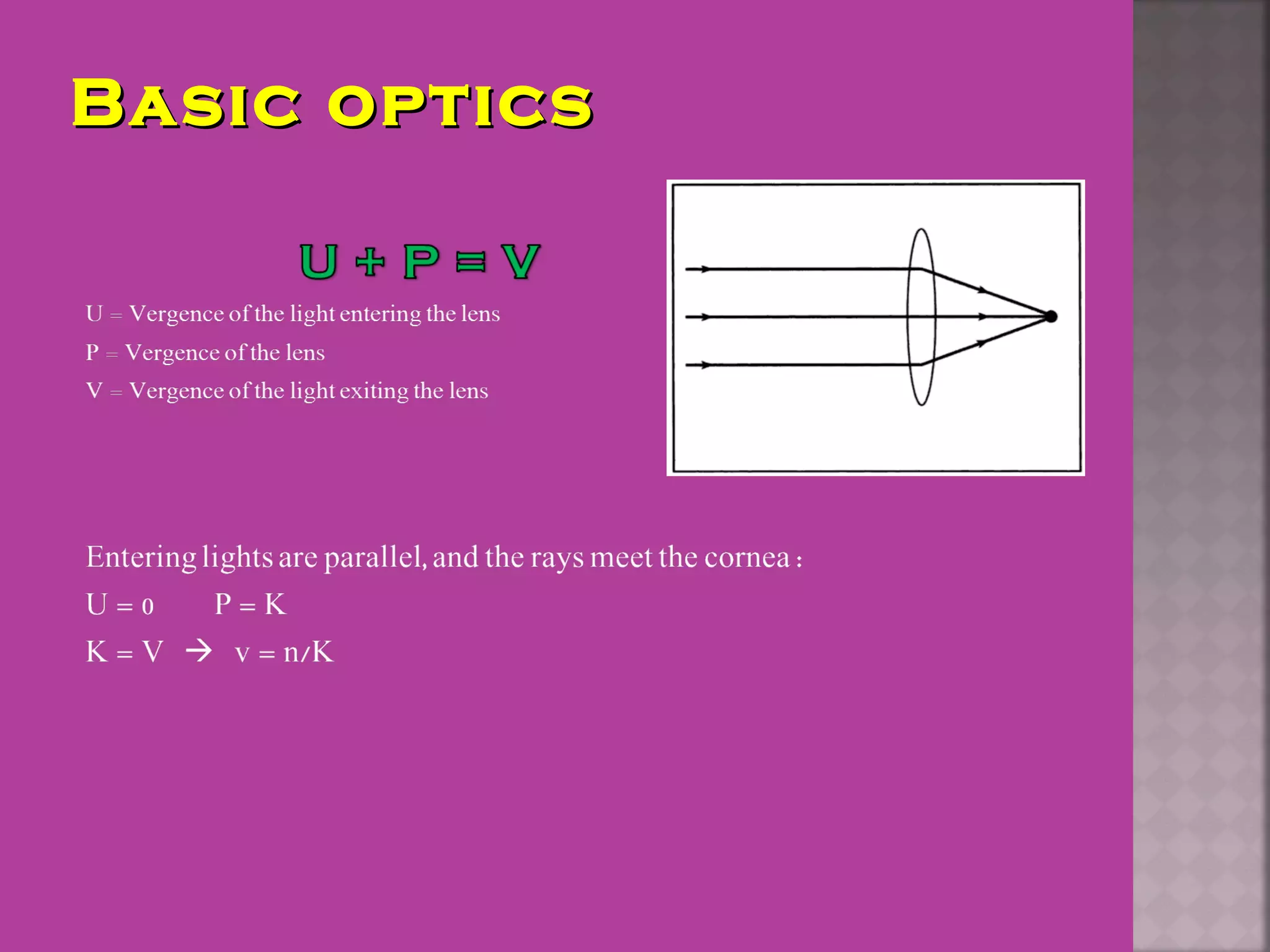
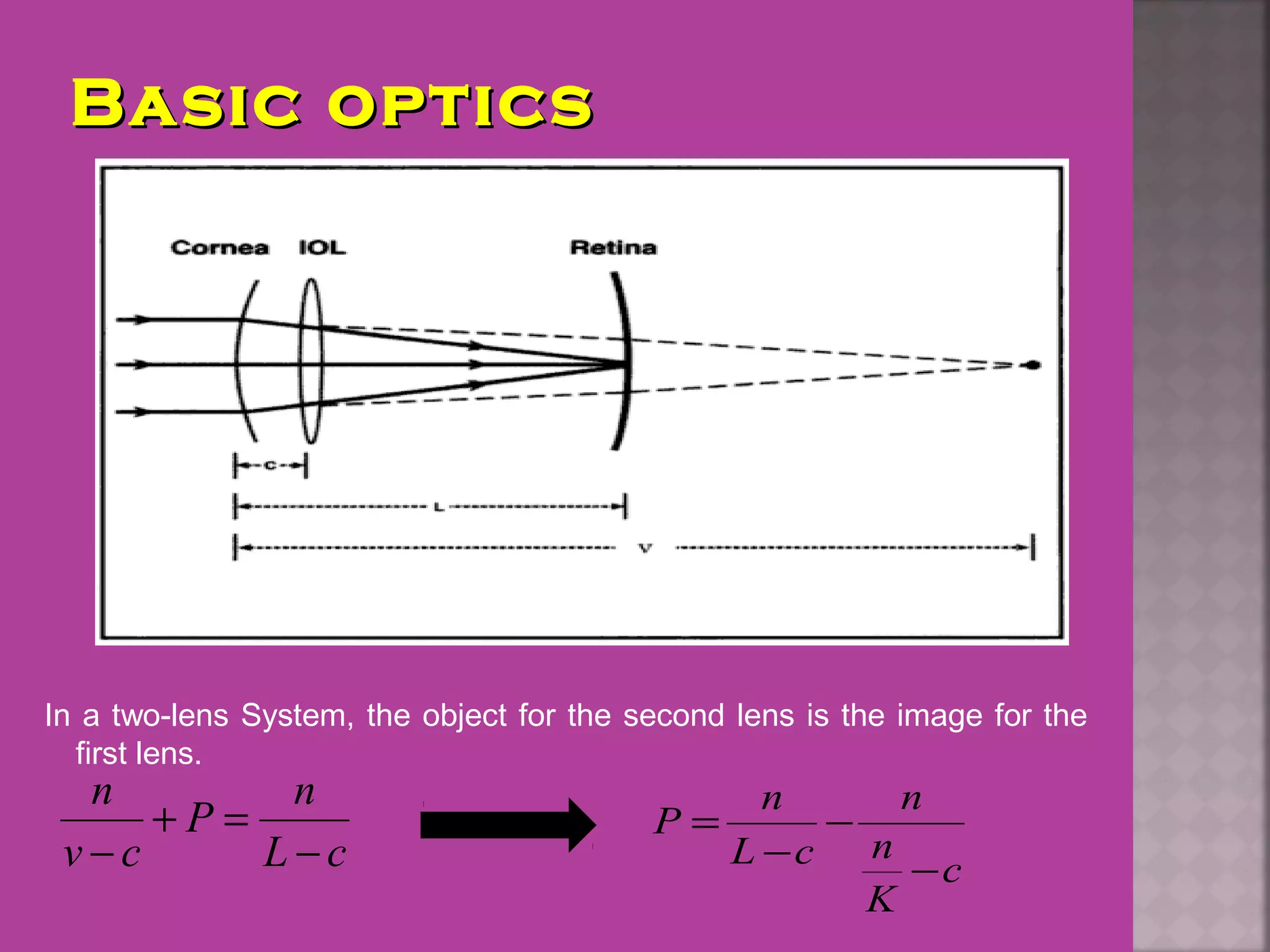
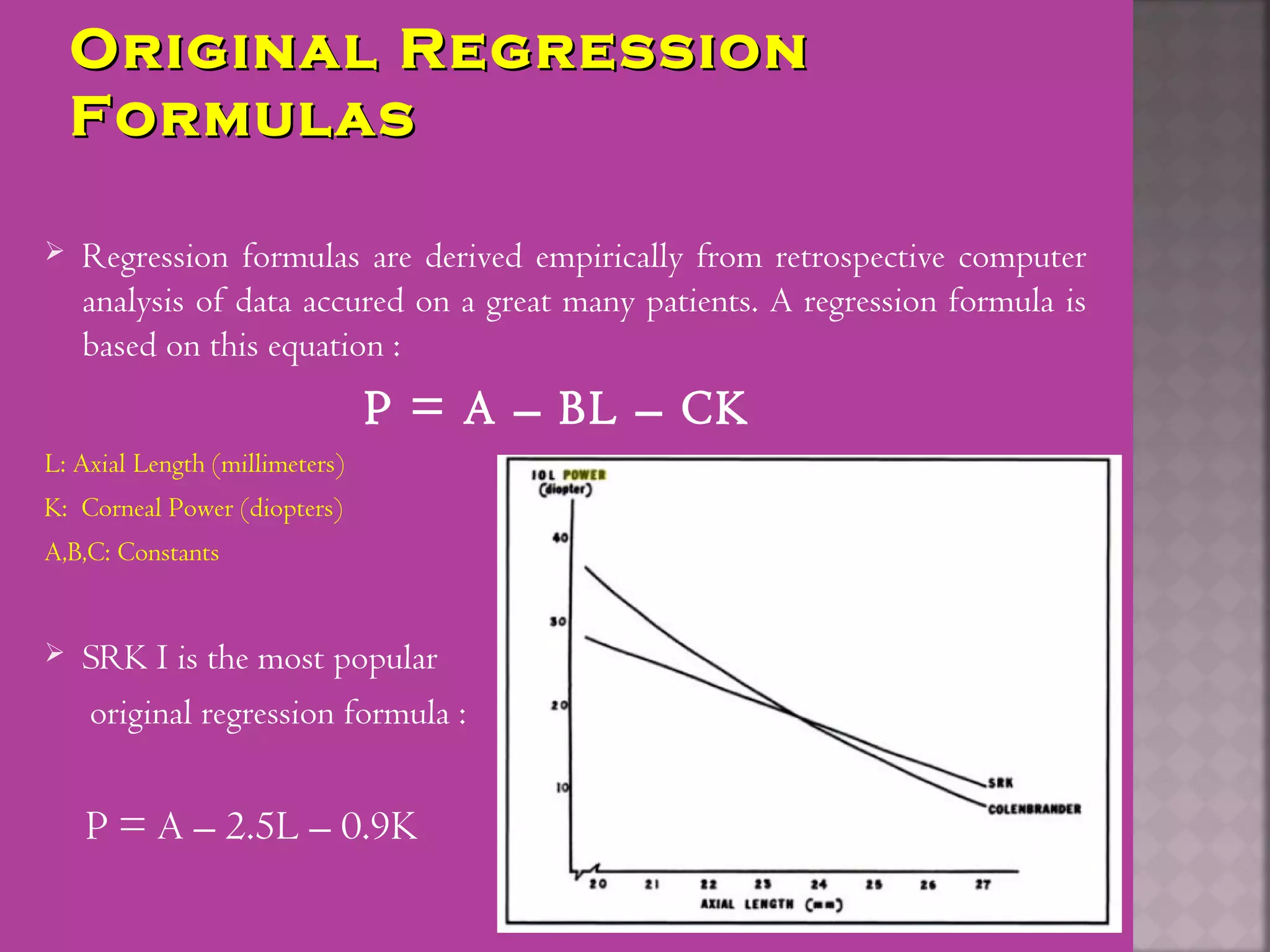
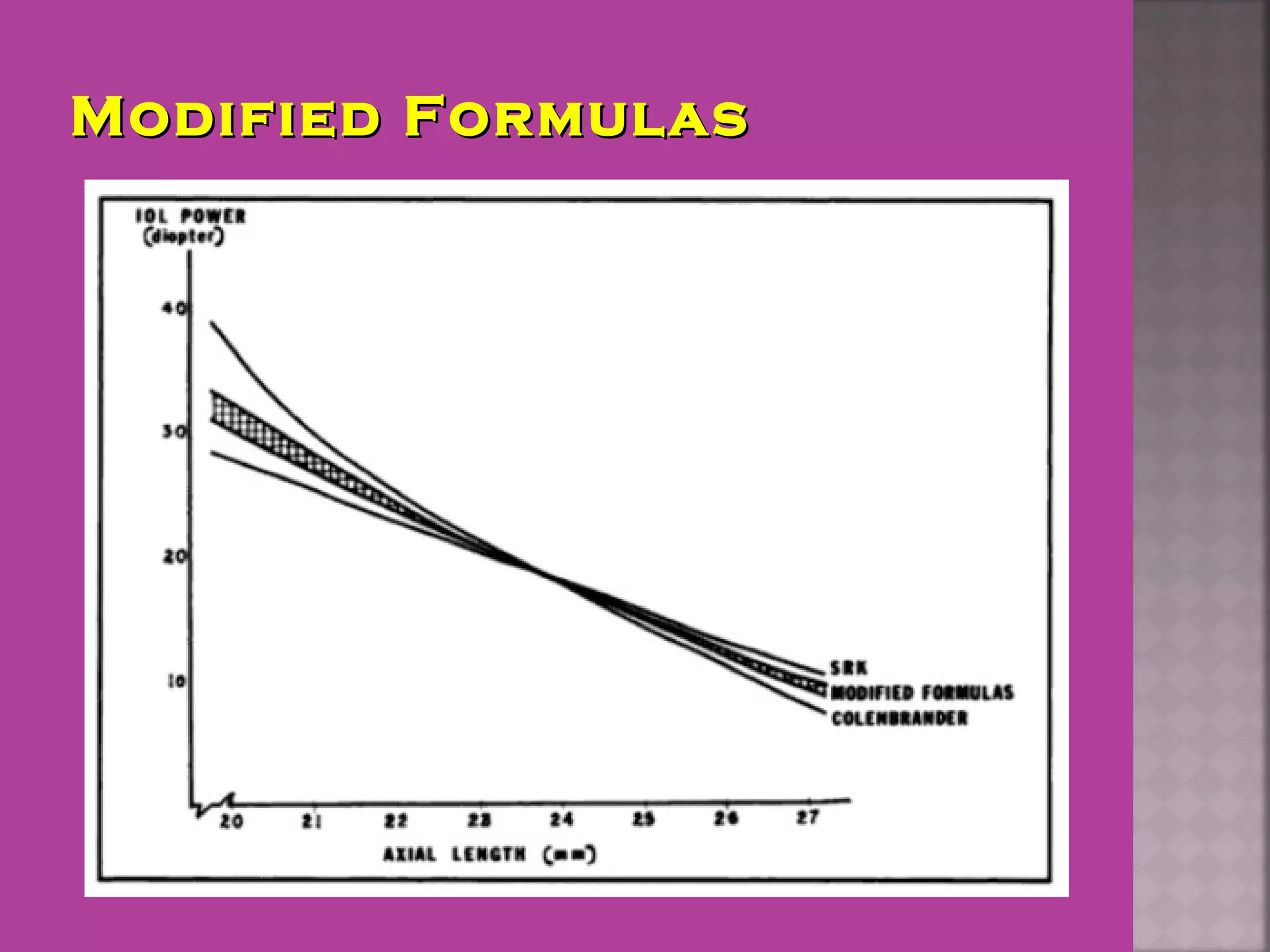
This document discusses the history and evolution of intraocular lens (IOL) power calculation methods. It begins by describing problems with pre-IOL era cataract treatment using thick "Coke bottle bottom" spectacles. The first successful IOL implantation was performed by Sir Harold Ridley in 1949 using a PMMA lens. Early IOL power calculations often had errors over 1 diopter. The document then covers the development of theoretical formulas, regression formulas like SRK I, and modified formulas like Holladay I and Haigis that incorporate additional ocular measurements like axial length, corneal power, and anterior chamber depth to improve accuracy. Modern devices like the IOL Master and Lenstar are also able to precisely measure these parameters to

1. A.H. Mirfendereski
Tehran University of Medical Sciences
Optometry Department

2. Pre-IOL era :
 Patients traded in their cataractous lenses for “Coke bottle bottom”
spectacles.
 Problems :
 Prismatic effect and ring scotoma between 40 and 60 degrees.
 Markedly constricted visual field.
 Lack of stereopsis.
 Spherical aberrations.
 False orientation.
 As early as the 1760s, ophthalmologists had explored the idea
of an artificial replacement for the cataractous lens.
 Around 1795, Casamata inserted a glass lens into an eye, but it
immediately sank back toward the posterior pole.

3. IntroductionIntroduction
 Sir Harold Ridley was the first to successfully implant
an intraocular lens in 1949. The procedure was
performed on a 45-year-old woman at St Thomas
Hospital at London.
 That first IOL was manufactured by the Rayner
company from PMMA.
 The surgery was an anatomic success, but the patient
was left highly myopic.
 Her postoperative visual acuity was 6/18, requiring a
refractive correction of -18.0 -6.0 × 120. There
was clearly an error in the calculation.
 Baron designed and implanted the first Anterior
Chamber IOL (ACIOL) in 1952.

4. IntroductionIntroduction

7. Clinical historyClinical history
MethodMethod
 Before 1975 the power of an IOL was calculated by the use of this
equation :
P = 18 + ( 1.25 × Ref )
 Errors exceeding 1 diopter occurred in over 50% of cases.
 These large errors were caused by the difficualty of determining the
patients' refractive error,

8. Power CalculationPower Calculation
FormulasFormulas

9. Basic opticsBasic optics

10. Basic opticsBasic optics
In a two-lens System, the object for the second lens is the image for the
first lens.
cL
n
P
cv
n
−
=+
− c
K
n
n
cL
n
P
−
−
−
=

11. Original TheoriticalOriginal Theoritical
FormulasFormulas
Required Measurements :
 L : The Axial Length in millimeters.
 C : The estimated postoperative anterior chamber depth (ACD) in
millimeters.
 K: The corneal power in diopters.
 r : The corneal radius of curvature.

12. Original RegressionOriginal Regression
FormulasFormulas
 Regression formulas are derived empirically from retrospective computer
analysis of data accured on a great many patients. A regression formula is
based on this equation :
P = A – BL – CK
L: Axial Length (millimeters)
K: Corneal Power (diopters)
A,B,C: Constants
 SRK I is the most popular
original regression formula :
P = A – 2.5L – 0.9K

13. Modified FormulasModified Formulas
1000
05.0336.1
336.1
05.0
1336
+
−
+
−
−−
=
C
RK
CL
P
1336
05.00125.1
1
05.0)23(1.0
1336
+
−
−
−−−−
=
C
K
CLL
P

14. Modified FormulasModified Formulas
)4)((
)4(1336
CRCL
LR
P
−−
−
=
KLAP 9.05.21 −−=

15. Modified FormulasModified Formulas

17. Estimated Lens PositionEstimated Lens Position
(ELP)(ELP)

18. Estimated Lens PositionEstimated Lens Position
(ELP)(ELP)
(1/23.45)12.5LengthAxialAG
)]4/1)((AGR[R0.56aACD
SaACDELP
222
××=
−+=
+=
−
3.595-0.9704)value(ACDfactorS
65.60-0.5663)constant-(AfactorS
×=
×=

23. The Haigis FormulaThe Haigis Formula
)()(
positionlenseffectivethe
210 ALaACDaad
d
×+×+=
=

25. Measuring The Axial LengthMeasuring The Axial Length

26. A-SCANA-SCAN

27. A-SCANA-SCAN
Community Eye Health Journal Vol. 19 No. 60 DECEMBER 2006 www.cehjournal.org
J Emmetropia 2011; 2: 210-216 ©2011 SECOIR - Sociedad Española de Cirugía Ocular Implanto-Refractiva

28. A-SCANA-SCAN

29. IOL MasterIOL Master

30. IOL MasterIOL Master
IOL MasterIOL Master
LenstarLenstar

31. 1.1. IOL Power CalculationsIOL Power Calculations, H. John Shammas, SLACK, H. John Shammas, SLACK
Incorporated, 2004Incorporated, 2004
2.2. Intraocular Lenses in Cataract and RefractiveIntraocular Lenses in Cataract and Refractive
SurgerySurgery,, Dimitri T. Azar. W.B. Saunders Company 2001Dimitri T. Azar. W.B. Saunders Company 2001
3.3. Lens Implant Power CalculationLens Implant Power Calculation, John A. Retzlaff,, John A. Retzlaff,
Slack Incorporated, 1990Slack Incorporated, 1990