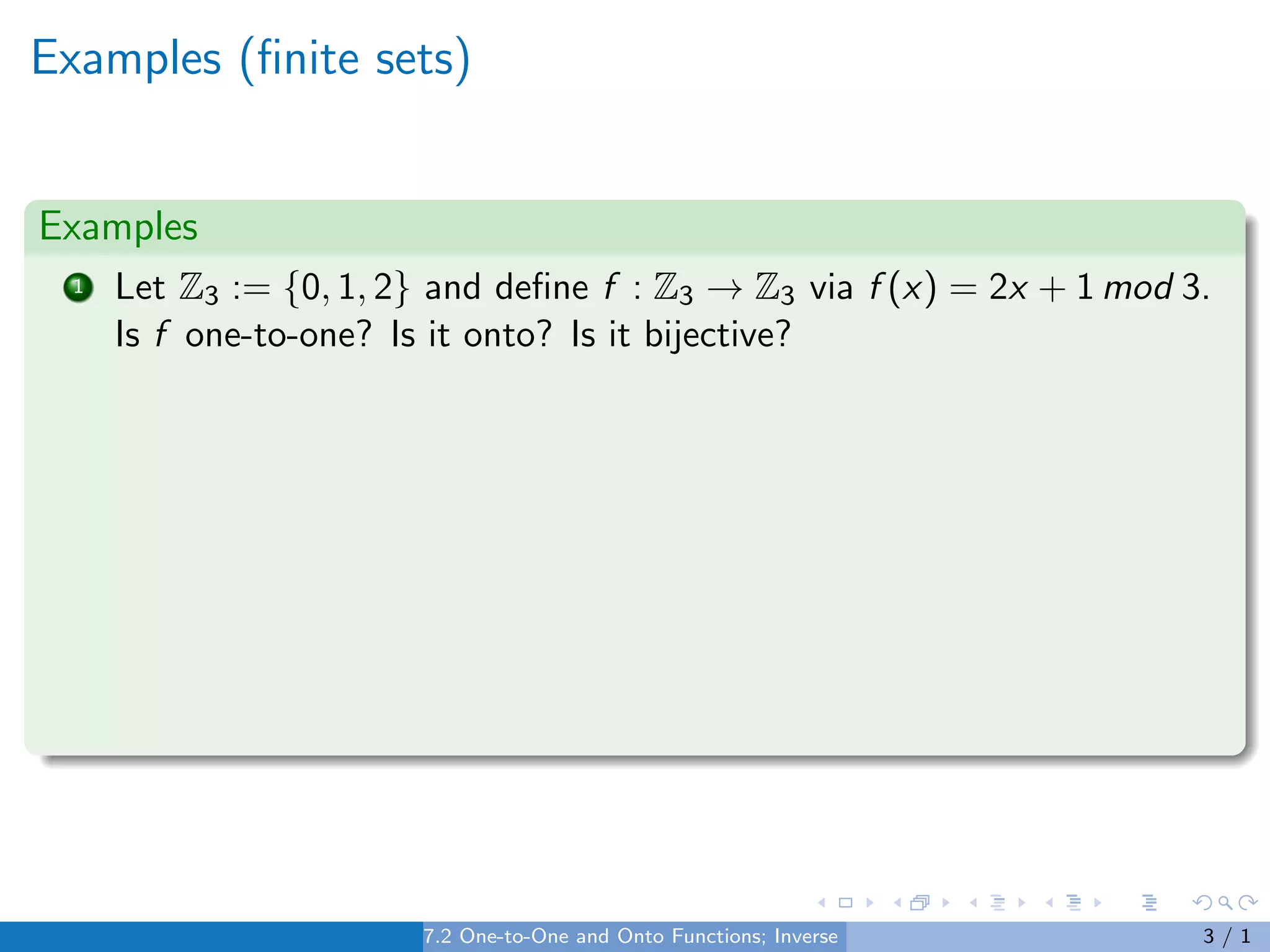
This document defines and provides examples of one-to-one, onto, and bijective functions. A one-to-one function maps distinct inputs to distinct outputs. An onto function maps the entire domain onto the range. A bijective function is both one-to-one and onto. The inverse of a bijective function is also discussed. Examples include functions from integers to integers and reals to reals.

1. 7.2 One-to-One and Onto Functions; Inverse Functions
7.2 One-to-One and Onto Functions; Inverse Functions 1 / 1

2. One-to-one, onto, and bijective functions
Definition
Let f : A → B be a function.
1 f is called one-to-one (injective) if a 6= a0 implies f (a) 6= f (a0).
7.2 One-to-One and Onto Functions; Inverse Functions 2 / 1

3. One-to-one, onto, and bijective functions
Definition
Let f : A → B be a function.
1 f is called one-to-one (injective) if a 6= a0 implies f (a) 6= f (a0).
2 f is called onto (surjective) if f (A) = B.
7.2 One-to-One and Onto Functions; Inverse Functions 2 / 1

4. One-to-one, onto, and bijective functions
Definition
Let f : A → B be a function.
1 f is called one-to-one (injective) if a 6= a0 implies f (a) 6= f (a0).
2 f is called onto (surjective) if f (A) = B.
3 f is called bijective (textbook notation: one-to-one correspondence)
if f is both one-to-one and onto.
7.2 One-to-One and Onto Functions; Inverse Functions 2 / 1

5. Examples (finite sets)
Examples
1 Let Z3 := {0, 1, 2} and define f : Z3 → Z3 via f (x) = 2x + 1 mod 3.
Is f one-to-one? Is it onto? Is it bijective?
7.2 One-to-One and Onto Functions; Inverse Functions 3 / 1

6. Examples (finite sets)
Examples
1 Let Z3 := {0, 1, 2} and define f : Z3 → Z3 via f (x) = 2x + 1 mod 3.
Is f one-to-one? Is it onto? Is it bijective?
2 Encoding and decoding functions: Recall from last time: A is the
set of all strings of 0’s and 1’s; T is the set of all strings of 0’s and
1’s that consist of consecutive triples of identical bits. The encoding
function E : A → T, E(s) =the string obtained from s by replacing
each bit of s by the same bit written three times, and the decoding
function D : T → A, D(t) =the string obtained from t by replacing
each consecutive triple of three identical bits of t by a single copy of
that bit. Are E and D one-to-one, onto, bijective functions?
7.2 One-to-One and Onto Functions; Inverse Functions 3 / 1

7. Examples (infinite sets)
Examples
1 Let f : Z → Z defined via f (n) = 2n. Prove that f is one-to-one but
not onto.
7.2 One-to-One and Onto Functions; Inverse Functions 4 / 1

8. Examples (infinite sets)
Examples
1 Let f : Z → Z defined via f (n) = 2n. Prove that f is one-to-one but
not onto.
2 Let f : R → R defined via f (x) = 3x − 1. Is f (x) one-to-one, onto,
bijective?
7.2 One-to-One and Onto Functions; Inverse Functions 4 / 1

9. Examples (infinite sets)
Examples
1 Let f : Z → Z defined via f (n) = 2n. Prove that f is one-to-one but
not onto.
2 Let f : R → R defined via f (x) = 3x − 1. Is f (x) one-to-one, onto,
bijective?
3 Let f : R → R defined via f (x) = x2. Is f (x) one-to-one, onto,
bijective? How do the answers change if we change the domain of the
function from R to R+?
7.2 One-to-One and Onto Functions; Inverse Functions 4 / 1

10. Inverse Functions
Fact
If f : A → B is a bijective function then there is a unique function called
the inverse function of f and denoted by f −1, such that
f −1
(y) = x ⇔ f (x) = y.
7.2 One-to-One and Onto Functions; Inverse Functions 5 / 1

11. Inverse Functions
Fact
If f : A → B is a bijective function then there is a unique function called
the inverse function of f and denoted by f −1, such that
f −1
(y) = x ⇔ f (x) = y.
Example
Find the inverse functions of the bijective functions from the previous
examples.
7.2 One-to-One and Onto Functions; Inverse Functions 5 / 1

12. Composition (part of section 7.3)
Definition
If f : A → B and g : B → C are functions, then we can define a function
g ◦ f : A → C called the composition of g and f such that
g ◦ f (x) = g(f (x)).
7.2 One-to-One and Onto Functions; Inverse Functions 6 / 1

13. Composition (part of section 7.3)
Definition
If f : A → B and g : B → C are functions, then we can define a function
g ◦ f : A → C called the composition of g and f such that
g ◦ f (x) = g(f (x)).
Examples
1 Let f : R → R and g : R → R be f (x) = 2x + 1 and g(x) = x2. Find
g ◦ f (x).
2 Let E and D be the encoding functions. Find D ◦ E(s) and E ◦ D(s).
7.2 One-to-One and Onto Functions; Inverse Functions 6 / 1

14. Composition (part of section 7.3)
Definition
If f : A → B and g : B → C are functions, then we can define a function
g ◦ f : A → C called the composition of g and f such that
g ◦ f (x) = g(f (x)).
Examples
1 Let f : R → R and g : R → R be f (x) = 2x + 1 and g(x) = x2. Find
g ◦ f (x).
2 Let E and D be the encoding functions. Find D ◦ E(s) and E ◦ D(s).
3 Important fact: If f : X → Y is a bijective function, then
f ◦ f −1 = IY and f −1 ◦ f = IX .
7.2 One-to-One and Onto Functions; Inverse Functions 6 / 1