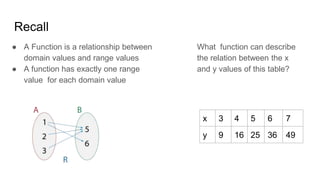
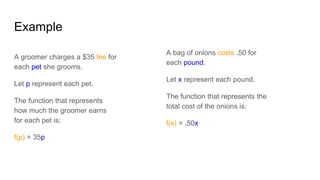
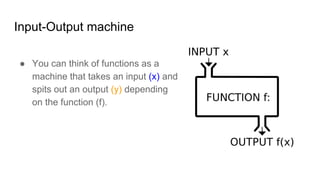
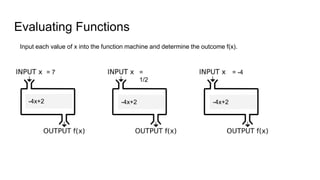
The document provides instruction on writing and understanding functions. It defines a function as a rule that assigns each input exactly one output. The independent variable is the input and is not dependent on any other variable, while the dependent variable is the output and depends on the input. Examples show identifying independent and dependent variables in situations. Function notation is introduced as a way to write the relationship between the input and output as f(x). Students practice evaluating functions by inputting values of x into the function rule. Real-world scenarios are used to demonstrate writing function rules.

1. Writing Functions
Unit 4
Algebra 1 - 8th grade
Ms. Martinez

2. Lecture Objective
CCSS.MATH.CONTENT.8.F.A.1
Understand that a function is a rule that assigns to each input exactly one output.
The graph of a function is the set of ordered pairs consisting of an input and the
corresponding output.
Lecture Objective: Identify and distinguish between independent and dependent
variables. Write an equation in function notation and evaluate that function.

3. Why are functions relevant to you?
Think about your first job and when you first start
making money.
How would you know how many hours you need to
work to afford that shirt, car, phone,etc that you
really want?

4. Recall
x 3 4 5 6 7
y 9 16 25 36 49
● A Function is a relationship between
domain values and range values
● A function has exactly one range
value for each domain value
What function can describe
the relation between the x
and y values of this table?

5. Independent vs. Dependent Variables
x y
3 9
4 16
5 25
6 36
7 49
● The input of this data is
the x values
● The output of this data is
the y values
● The input (x) is the
independent variable
and is not dependent
on any other
variable.
● The output (y) is
dependent on the
input x, it is the
dependent variable.

6. Video

7. Understanding Check
What are the independent and dependent variables in the following situations?
a. Mcdonalds is hiring and is paying their employees $15 an hour.
b. Tomatoes at the grocery store costs 79 cents a pound.

8. Function Rule
x relationship y
1 + (2) 3
2 + (2) 4
3 + (2) 5
4 + (2) 6
● An algebraic expression that represents
the relation between the domain and
range is called the function rule.
● The value of y is 2 more than x, so the
function rule for this data is: x+2 = y

9. Function Notation
● There are many ways to write functions, one method is function notation.
● In function notation, y is written as f(x) (‘f of x’), where f is the function
Ex: In our last slide we determined the function rule is:
y = x + 2
f(x) = x + 2
Since y is the dependent on x, function notation exists to show relationship
between the input (x) and output f(x).
Function notation

10. Example
A groomer charges a $35 fee for
each pet she grooms.
Let p represent each pet.
The function that represents
how much the groomer earns
for each pet is:
f(p) = 35p
A bag of onions costs .50 for
each pound.
Let x represent each pound.
The function that represents the
total cost of the onions is:
f(x) = .50x

11. Input-Output machine
● You can think of functions as a
machine that takes an input (x) and
spits out an output (y) depending
on the function (f).

12. Evaluating Functions
Input each value of x into the function machine and determine the outcome f(x).
= 7
-4x+2 -4x+2 -4x+2
=
1/2
= -4

13. Understanding Check
What are the independent and dependent variables in the following situations? Write a
rule in function notation.
a. Hank pays $50 a week plus $299 for his utilities.
b. Brenda sells her necklaces for $10 each, including tax.

14. World Application
● When using functions to describe real world scenarios, not every input makes
sense to use ex.(1,000 lbs of onions, or -3 pets per day)
Example:
Jake is selling his last 3 baseball cards. He is pricing them at $40 each. Write
a function rule that describes how much money Jake can make from selling
his cards.
● Reasonable domain: x = {1,2,3}
Cards (x) 1 2 3
Money Earned f(x) f(x) = 40(1)
= 40
f(x) = 40(2)
= 80
f(x) = 40(3)
= 120

15. Understanding Check
● Discuss with your group how to identify a independent
variable and a dependent variable in any given scenario.
● Name an example of a school related scenario that can be
described as a function. Label the independent and
dependent variables.