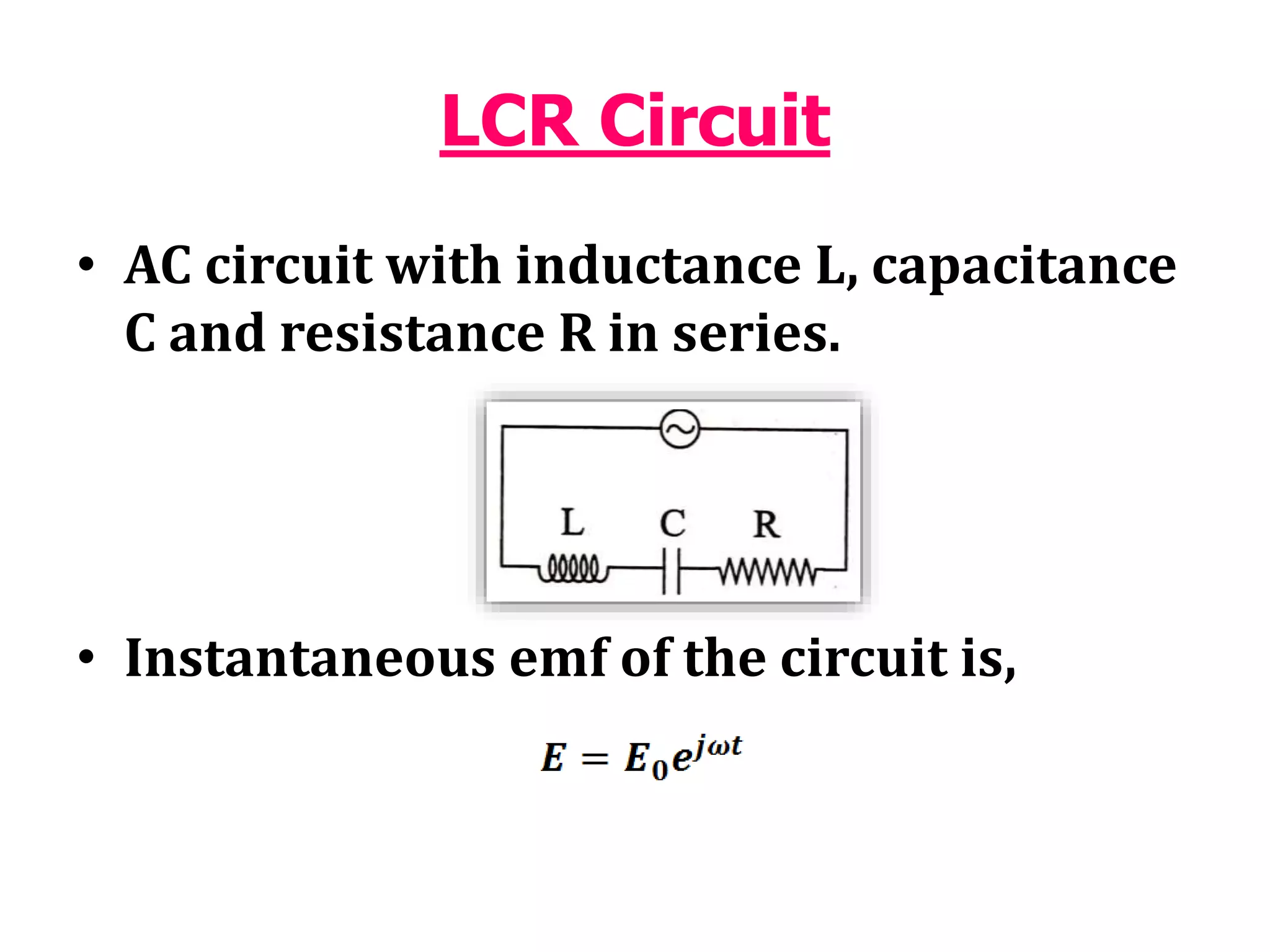
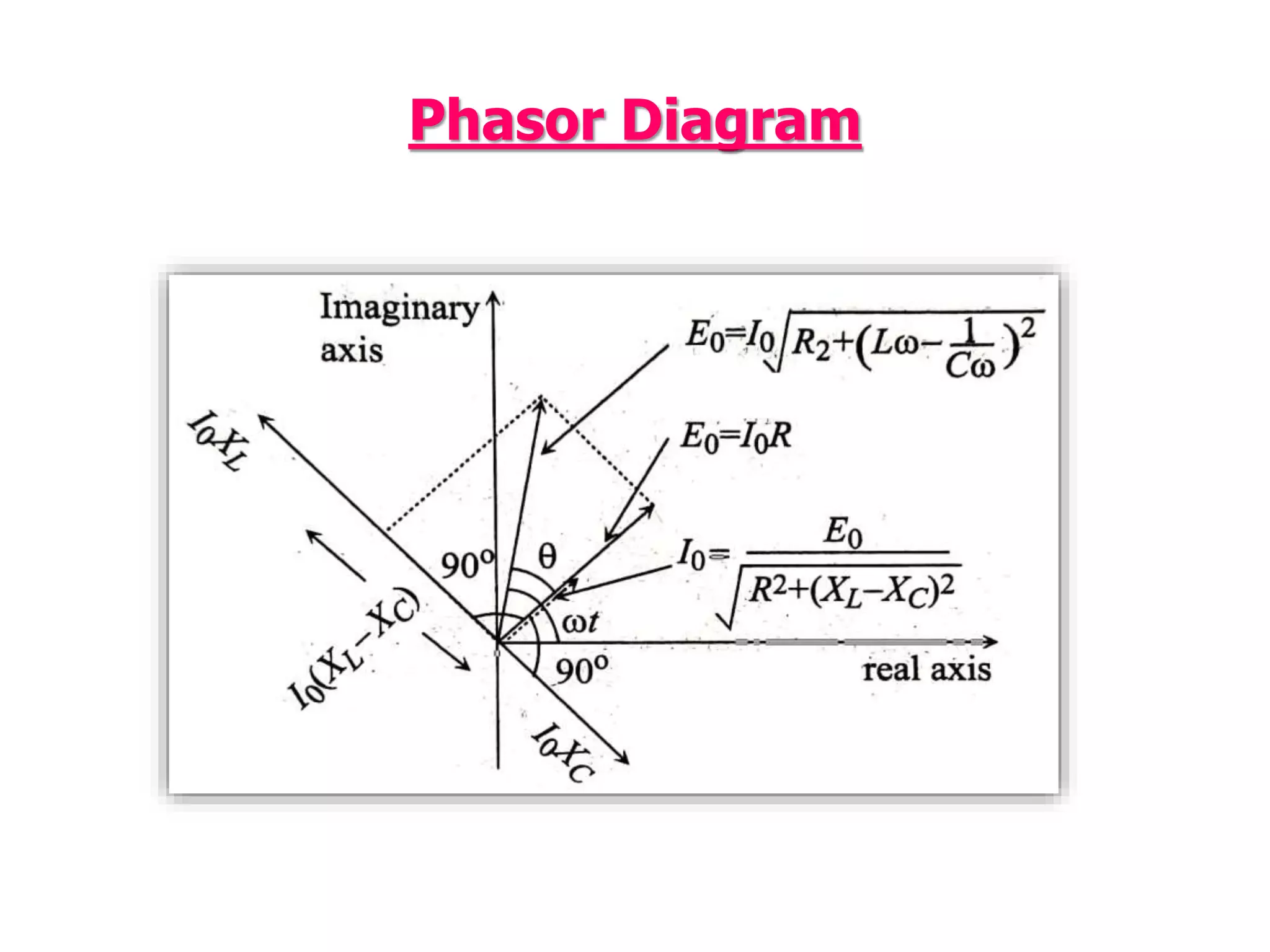
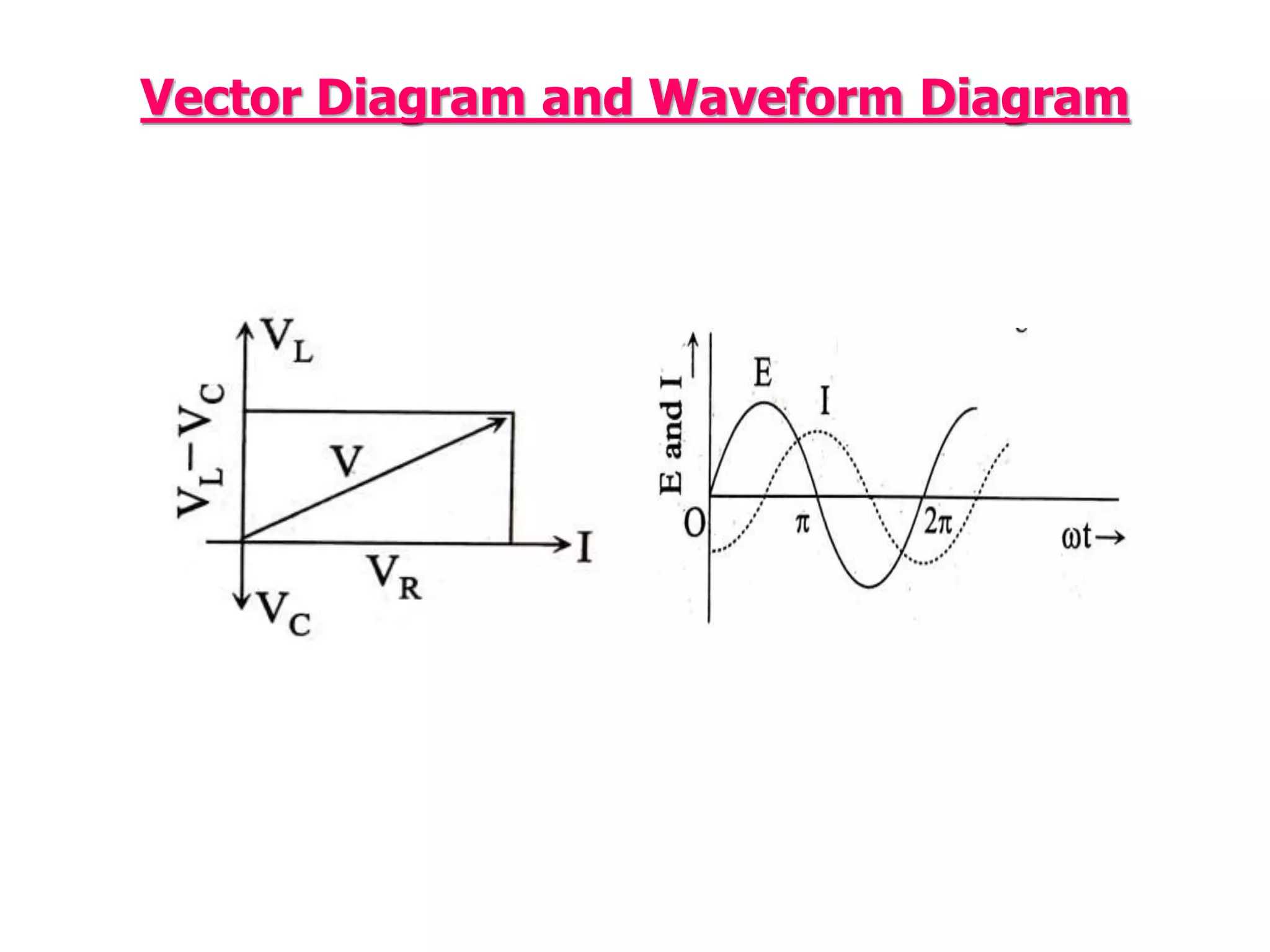
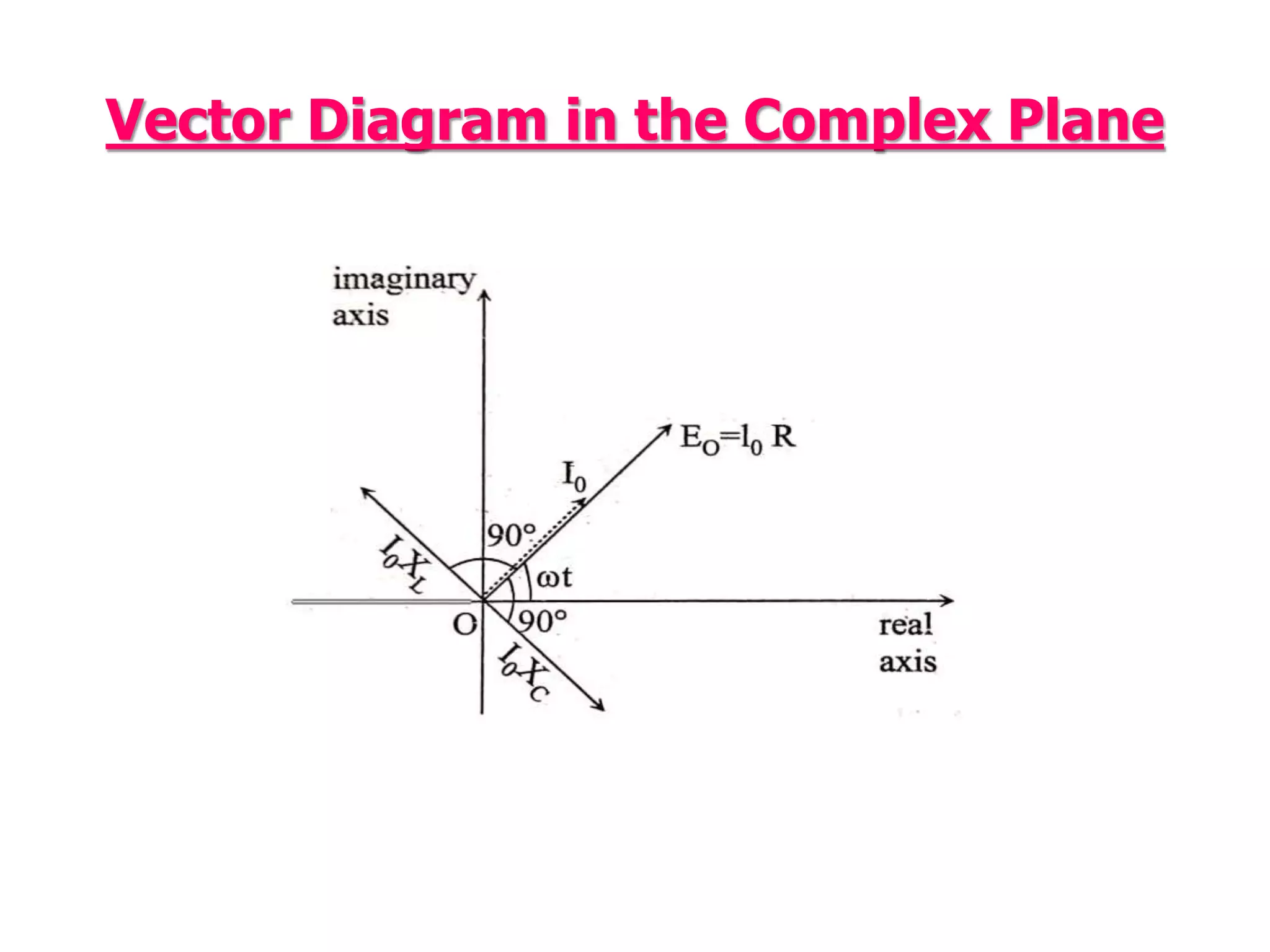
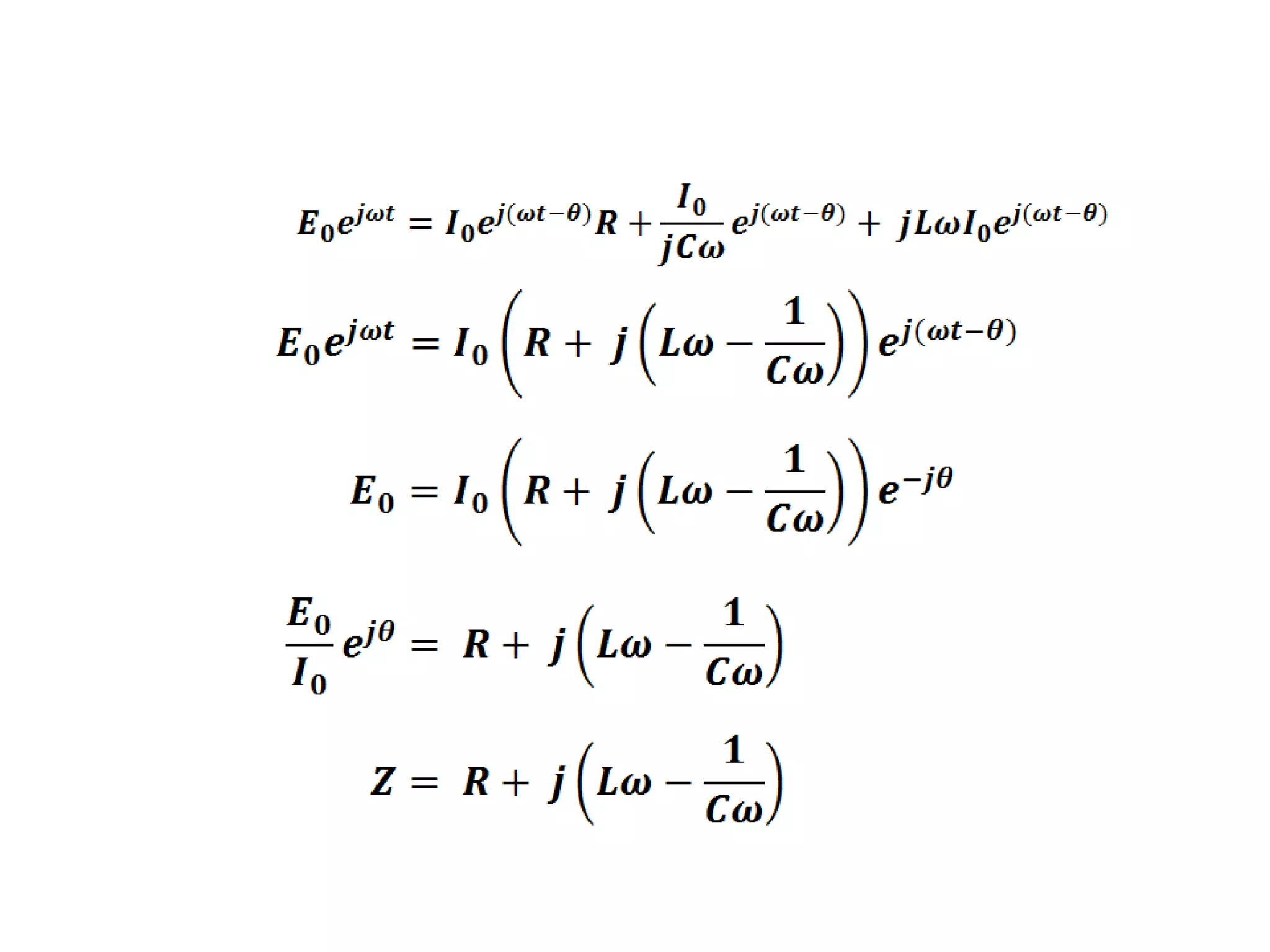This document discusses an AC circuit with inductance, capacitance, and resistance in series. It defines the circuit components and equations for current, impedance, and phase angle. Special cases are described where the circuit behaves as inductive, capacitive, or resistive depending on the phase relationship between current and applied emf. Resonance is explained as the condition when peak current is maximum and phase angle is zero.

1. AC CIRCUIT WITH
INDUCTANCE, CAPACITANCE
AND RESISTANCE IN SERIES
Syam Kumar S U
Assistant Professor
Department of Physics
N.S.S. College, Nilamel

2. LCR Circuit
• AC circuit with inductance L, capacitance
C and resistance R in series.
• Instantaneous emf of the circuit is,

3. The current in the circuit can be
expressed as
The complex impedance is given by
The value of Z can be obtained in terms
of the circuit parameters.
Applying Kirchhoff’s law to the loop,

5. The modulus of Z is given by
The argument of Z is given by

6. Phasor Diagram

7. Vector Diagram and Waveform Diagram

8. Special Cases
Case 1:
if the phase angle θ will be positive and
the current will lag behind the applied emf.
The potential difference across the inductance
is greater than potential difference across the
capacitance and the circuit behaves as an
inductive circuit.

9. Case 2:
If the phase angle will be negative
and the current will lead the applied emf.
The circuit behaves as a capacitive circuit.

10. Case 3:
If the phase angle θ becomes zero.
The emf and current will be in phase.
The potential difference across the
inductance and capacitance are equal in
magnitude but opposite in direction and
hence cancel out.
It behaves as a purely resistive circuit.

11. Vector Diagram in the Complex Plane

12. • Under this condition the peak current will be
maximum and is given by
• The circuit is said to be a series resonance
circuit and the phenomenon is called
resonance.