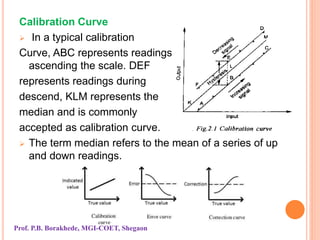
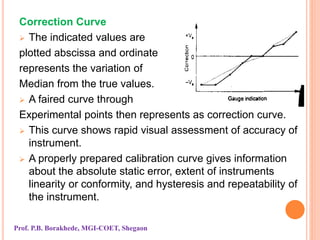
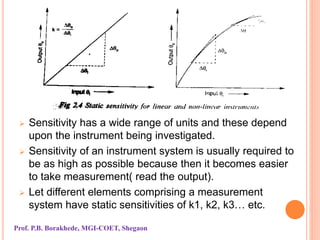
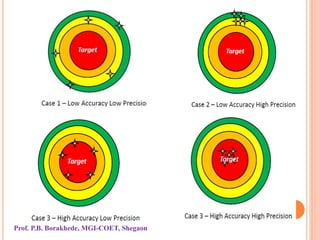
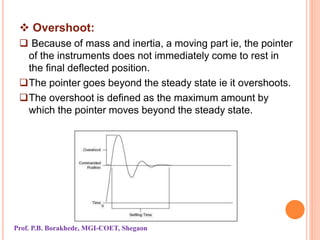
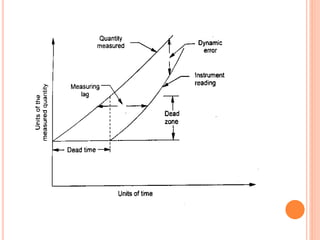
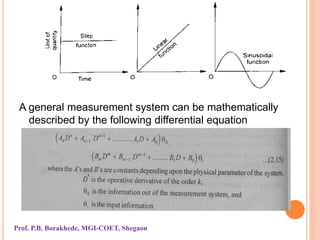
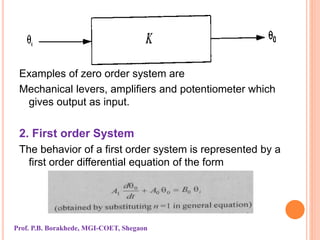
The document outlines instrument characteristics in measurement systems, focusing on static and dynamic performance. It highlights key qualities such as range, accuracy, error, correction, calibration, sensitivity, precision, repeatability, and dynamic behavior, including concepts like hysteresis and dead zones. Overall, it emphasizes the importance of understanding these characteristics to enhance the accuracy and reliability of measuring instruments.