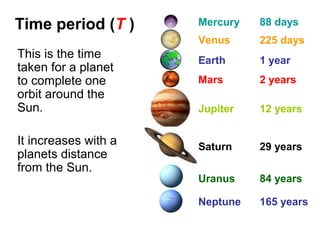
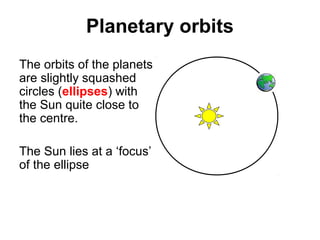
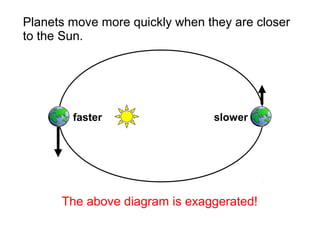
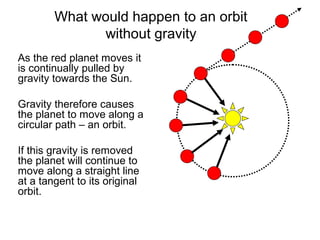
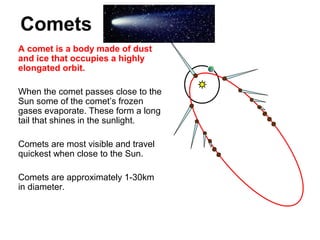
The document provides information about the Solar System, including its planets, dwarf planets, asteroids, moons, comets, and orbital properties. It details the eight major planets in order from the Sun, as well as dwarf planets and asteroids. Key facts about moons, orbital periods, speeds, and gravitational forces are summarized. Examples of communication satellites and galaxies are also briefly described.

1. Astronomy

2. The Solar System
The Solar System consists of the Sun orbited by eight
planets and their moons, some dwarf planets along with
many asteroids and comets.

3. Planets
A planet is a body that orbits
the Sun, is massive enough
for its own gravity to make it
round, and has cleared its
neighbourhood of smaller
objects around its orbit.
Based on this, International
Astronomical Union’s definition
of 2006, there are only eight
planets in orbit around the
Sun.
In order of distance
from the Sun:
Mercury
Venus
Earth
Mars
Jupiter
Saturn
Neptune
Uranus

4. Dwarf Planets
A dwarf planet is a celestial
body orbiting the Sun that is
massive enough to be
spherical as a result of its own
gravity. but has not cleared its
neighbouring region of other
similar bodies.
As of 2011 there are five dwarf
planets in the Solar System.
Between Mars and Jupiter:
Ceres
Beyond Neptune:
Pluto, Haumea,
Makemake
and Eris (the largest)

6. Asteroids
An asteroid is a celestial body
orbiting the Sun that is not
massive enough to be spherical
as a result of its own gravity.
Most asteroids are found between
the orbits of Mars and Jupiter – a
region called ‘The Asteroid Belt’.
There are about 750 000 asteroids
larger than 1km across.
A few, called ‘Near Earth
Asteroids’ can pass very close to
the Earth.
Asteroid Vesta – image
taken on July 17th
2011 by
the Dawn spacecraft

7. Moons
A moon orbits a planet.
Planet Moons (2011)
Mercury 0
Venus 0
Earth 1
Mars 2
Jupiter 64
Saturn 62
Uranus 27
Neptune 13
The Earth’s only
natural satellite
Note: A number of dwarf planets and asteroids also have
moons, for example Pluto has three moons.

8. This is the time
taken for a planet
to complete one
orbit around the
Sun.
It increases with a
planets distance
from the Sun.
Mercury 88 days
Venus 225 days
Earth 1 year
Mars 2 years
Jupiter 12 years
Saturn 29 years
Neptune 165 years
Uranus 84 years
Time period (T )

9. Gravitational attraction
The force of gravity is responsible for the orbits of
planets, moons, asteroids and comets.
In 1687 Sir Isaac Newton stated that this
gravitational force:
- is always attractive
- would double if either the mass of Sun or
the planet was doubled
- decreases by a factor of 4 as the distance
between the Sun and a planet doubles.

10. Gravitational field strength (g)
This is a way of measuring the strength of gravity.
The gravitational field strength is equal to the
gravitational force exerted per kilogram.
Near the Earth’s surface, g = 10 N/kg
In most cases gravitational field strength in N/kg is
numerically equal to the acceleration due to
gravity in m/s2
, hence they both use the same
symbol ‘g’.

11. Gravitational field strength (g) varies from planet
to planet.
It is greatest near the most massive objects.

12. Planetary orbits
The orbits of the planets
are slightly squashed
circles (ellipses) with
the Sun quite close to
the centre.
The Sun lies at a ‘focus’
of the ellipse

13. Planets move more quickly when they are closer
to the Sun.
faster slower
The above diagram is exaggerated!

14. What would happen to an orbit
without gravity
As the red planet moves it
is continually pulled by
gravity towards the Sun.
Gravity therefore causes
the planet to move along a
circular path – an orbit.
If this gravity is removed
the planet will continue to
move along a straight line
at a tangent to its original
orbit.

15. Comets
A comet is a body made of dust
and ice that occupies a highly
elongated orbit.
When the comet passes close to the
Sun some of the comet’s frozen
gases evaporate. These form a long
tail that shines in the sunlight.
Comets are most visible and travel
quickest when close to the Sun.
Comets are approximately 1-30km
in diameter.

16. Halley’s Comet
This is perhaps the most
famous comet.
It returns to the inner Solar
System every 75 to 76 years.
It last appeared in 1986 and is
due to return in 2061.
It has been observed since at
least 240BC. In 1705 Edmund
Halley correctly predicted its
reappearance in 1758.

17. Orbital speed (v)
orbital speed = (2π x orbital radius) / time period
v = (2π x r ) / T
orbital speed in metres per second (m/s)
orbital radius in metres (m)
time period in seconds (s)

18. Communication satellites
These are usually placed in geostationary orbits
so that they always stay above the same place on
the Earth’s surface.
VIEW FROM
ABOVE THE
NORTH POLE

19. Geostationary satellites must have orbits that:
- take 24 hours to complete
- circle in the same direction as the Earth’s
spin
- are above the equator
- orbit at a height of about 36 000 km
Uses of communication satellites include satellite
TV and some weather satellites.

20. The Milky Way
The Milky Way is the
name of our galaxy.
From Earth we can see
our galaxy edge-on. In a
very dark sky it appears
like a ‘cloud’ across the
sky resembling a strip of
spilt milk.
A very dark sky is required to
see the Milky Way this clearly

21. Galaxies
Galaxies consist of billions
of stars bound together by
the force of gravity.
There are thought to be at
least 200 billion galaxies
in our Universe each
containing on average 2
billion stars.
Types of galaxy-
spiral,elliptical.irregular
The Andromeda Galaxy

22. Question 1
Calculate the orbital speed of the Earth around the Sun.
(Earth orbital radius = 150 million km)
v = (2π x r ) / T
= (2π x [150 000 000 km] ) / [1 year]
but 1 year = (365 x 24 x 60 x 60) seconds
= 31 536 000 s
and 150 000 000 km = 150 000 000 000 metres
v = (2π x [150 000 000 000] ) / [31 536 000]
orbital speed = 29 900 m/s

23. Question 2
Calculate the orbital speed of the Moon around the Earth.
(Moon orbital radius = 380 000 km; orbit time = 27.3 days)
v = (2π x r ) / T
= (2π x [380 000 km] ) / [27.3 days]
but 27.3 days = (27.3 x 24 x 60 x 60) seconds
= 2 359 000 s
and 380 000 km = 380 000 000 metres
v = (2π x [380 000 000] ) / [2 359 000]
orbital speed = 1 012 m/s

24. Question 3
Calculate the orbital speed of the ISS (International Space Station)
around the Earth. (ISS orbital height = 355 km; orbit time = 91 minutes;
Earth radius = 6 378 km)
The orbit radius of the ISS = (355 + 6 378) km = 6 733 km
v = (2π x r ) / T
= (2π x [6 733 km] ) / [91 minutes]
but 91 minutes = (91 x 60) seconds
= 5 460 s
and 6 733 km = 6 733 000 metres
v = (2π x [6 733 000] ) / [5 460]
orbital speed = 7 748 m/s

25. Question 4
Calculate the orbital time of a satellite that has a speed of 3 075 m/s
and height above the earth of 35 906 km. (Earth radius = 6 378 km)
The orbit radius of the satellite = (35 576 + 6 378) km = 42 284 km
v = (2π x r ) / T
becomes: T = (2π x r ) / v
= (2π x [42 284 km] ) / [3 075 m/s]
but 42 284 km = 42 284 000 metres
T = (2π x [41 954 000 ] ) / [3 075 ]
orbital time = 86 400 seconds
= 1440 minutes
= 24 hours