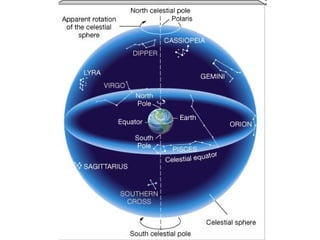
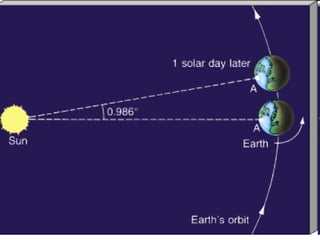
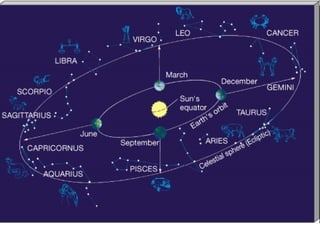
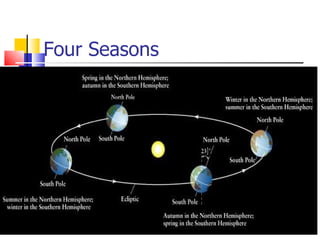
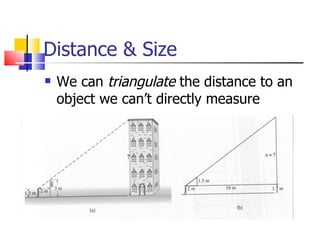
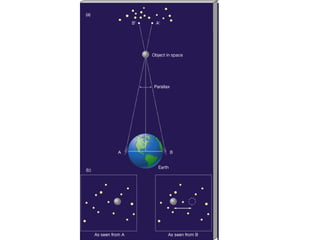
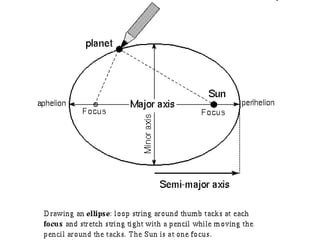
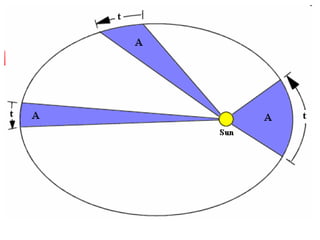
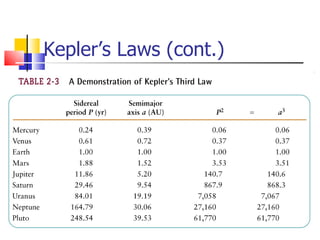
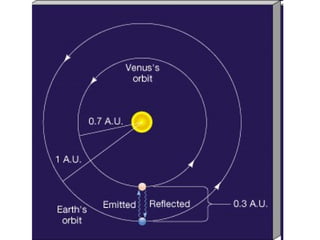
The document provides an introduction to astronomy, covering topics such as distances and measurements used in astronomy, motions of celestial objects, and key concepts like the celestial sphere and Kepler's laws of planetary motion. It describes units like the astronomical unit and light-year used to measure vast distances in space. Seasonal changes are explained by the tilt of Earth's axis and orbit around the Sun.

1. Intro to Astronomy

2. Space is Big For distances within our solar system, we use a unit of distance known as the Astronomical Unit (AU). 1 AU is defined as the average distance from the Earth to the Sun, roughly 1.5 x 10 8 kilometers (93 million miles)

3. Really Big When dealing with objects outside of our solar system, the AU is too small to be effective, so we use the light-year. A light-year (ly) is defined as the distance a beam of light travels in one year. 1 ly = 10 trillion km (6 trillion mi)

4. For Comparison... It takes a beam of light roughly 8 minutes to travel from the Sun to the Earth Proxima Centauri (the nearest star to us, after our Sun) is over 4 light years away

5. The Celestial Sphere Imagine the Earth at the center of a clear, hollow globe with the stars glued to the inside. Everything we use to navigate on Earth can be “copied” onto the Celestial Sphere (latitude, longitude, the equator, and the poles)

7. Angular Measurement A full circle contains 360 degrees 1 o can be broken further into arc minutes (60’ in 1 o ) Arc minutes can be broken again into arc seconds (60” in 1’)

8. Angular Measures The Sun and Moon both cover an area of about 0.5 o – half the size of a finger held at arm’s length At arm’s length, a hand spans about 15 o (also the amount of sky covered by the Sun’s motion in one hour)

9. Celestial Coordinates Declination (dec) is the equivalent of latitude on the Celestial Sphere dec is measured in degrees north or south of the Celestial Equator

10. Celestial Coordinates (cont.) Right Ascension (RA) is the longitude equivalent on the C.S. RA is measured in hours, minutes, and seconds The Prime Meridian of RA is wherever the Sun is on the C.S. at the vernal equinox (first day of spring)

11. Orbital Motion Solar Day: the time it takes the Sun to return to a specific spot in the sky (24 hours) Sidereal Day: the time it takes Earth to complete one full rotation in its orbit (23 hours, 56 minutes) The 4 minute per day difference gives us leap years

13. Seasonal Changes Earth’s orbit around the Sun causes us to see different constellations in the sky

14. The Zodiac The ecliptic is the Sun’s path along the Celestial Sphere. The Zodiac is made up of the 12 constellations that the Sun travels through along the ecliptic. Due to position, the constellation of your sign can only be seen 6 months before/after your birth month.

16. Seasonal Changes (cont.) Earth rotates on its axis, which is tilted 23 ½ degrees to its orbit. On the Celestial Sphere, the ecliptic is tilted the same 23 ½ degrees. This tilt is what gives us the four seasons.

17. Four Seasons

18. Four Seasons (cont.) Vernal Equinox – March 21st Autumnal Equinox – September 21 st 12 hours of night and day - everywhere Summer Solstice – June 21 st Most sunlight of the year Winter Solstice – December 21 st Least sunlight of the year

19. Distance & Size We can triangulate the distance to an object we can’t directly measure

20. Distance & Size (cont.) With really large distances, triangulation less reliable. Rather than used a measure baseline, we use the missing angle of the triangle, or parallax

21. Distance & Size (cont.) Try this: Hold a pencil in front of your face and let your eyes focus on the wall. First close your left eye, and then open it and close your right eye. The apparently difference in position of the pencil is parallax

23. Review By this point, you should be able to: Describe the Celestial Sphere Use angular measurements to find objects in space Explain the apparent motion of the Sun and stars with the actual motion of the Earth Explain how to gauge size and distance of faraway object

24. Motions of the Planets ‘ Planets’ comes from the Greek word: ‘planetes’ which means “wanderer” As viewed from Earth, the planets of our solar system all exhibit retrograde motion Like the Moon, planets are visible because of reflected sunlight

25. The Geocentric Universe Until the 16 th century, astronomers believed that the Earth was the center of the universe As a result, everything (the Sun, Moon, planets and stars) revolved around us Astronomers tried everything to fit observations into this theory

26. The Heliocentric Model Nicholas Copernicus proposed the idea of a Sun-centered universe in the 16 th century In fear of persecution, Copernicus kept his ideas secret until he died in 1543

27. Galileo & Kepler Galileo Galilei was the first astronomer to use a telescope for observing the night sky Using his telescope, he discovered: Sunspots Lunar terrain Moons orbiting Jupiter The phases of Venus

28. Eppur si muove For supporting Copernicus’ ideas, Galileo was arrested and sentenced to death He was spared the ultimate punishment and instead sentenced to house arrest for retracing his claims Supposedly, he muttered “And yet, it moves” under his breath after he recanted

29. Kepler’s Laws The planets revolve around the Sun in elliptical (not circular) paths Perihelion: when a planet is closest to the Sun Aphelion: when a planet is farthest from the Sun

31. Kepler’s Laws (cont.) Planetary orbits sweep out equal areas of the ellipse in equal amounts of time

33. Kepler’s Laws (cont.) The square of an orbital period is proportional to the cube of its semi-major axis P 2 (in Earth years) = a 3 (in AU)

34. Kepler’s Laws (cont.)

35. Kepler’s Laws (cont.) During Kepler’s life, there were only 6 known planets – those that can be seen without a telescope Kepler’s 3 rd Law works for Uranus, Neptune, and Pluto even though these were discovered after the 3 rd law was written!

36. Solar System Dimensions Recall: the astronomical unit is defined as the mean (average) distance from the Earth to the Sun This was done because until recently, we lacked the technology to directly measure distances outside of Earth

37. Dimensions (cont.) Today, we use radar imaging to directly measure the distance between planets We send radio waves toward a nearby object (Venus, for example) and wait for the echo to come back Multiply the round trip travel time by the speed of light and we calculate double the distance to the object

39. Example: Venus At its closest, Venus is 0.3 AU from Earth A RADAR signal takes 300 s to reach Venus and return to Earth 300,000 km/s * (300 s / 2) = 45,000,000 km = 0.3 AU Therefore, 1 AU = 150,000,000 km

40. Gravity The force due to gravity is continuous and always attractive Unlike magnets, there is no ‘repulsive’ gravity

41. Gravity (cont.) All objects constantly exert a gravitational force on each other – even you and me. The force is only dependent on the mass of the objects and the distance between them

42. Newton’s Law of Gravitation F = Gravitational Force G = Gravitational Constant = 6.67 x 10 -11 N m 2 / kg 2 M 1 = Mass of object #1 m 2 = Mass of object #2 r = Distance between objects

43. Important Notes The force decreases exponentially with distance If you’re twice as far away, the force is 2 2 times weaker (1/4 as strong) No matter how big r gets, the force never reaches zero (gravity exerts an effect everywhere)

44. Example: The Lunar Diet How much would you weigh on the Moon? F = Force or Weight G = Gravitational Constant = 6.67 x 10 -11 N m 2 / kg 2 M 1 = Mass of the Moon (7.3477×10 22 kg) m 2 = Mass of you (~70kg) r = 1,737,000 m (Moon radius)

45. Example (cont.) This compares to a weight on Earth of: W = (70 kg) * (9.8 m/s 2 ) = 686 N Or, roughly, you’d weigh 1/6 as much on the Moon