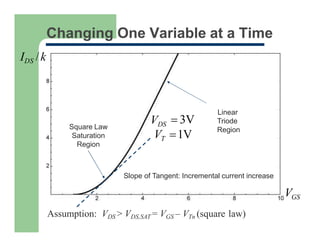
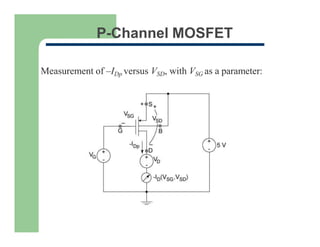
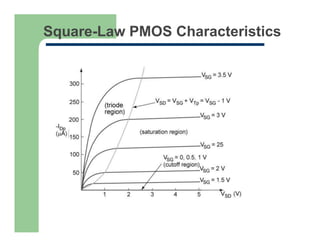
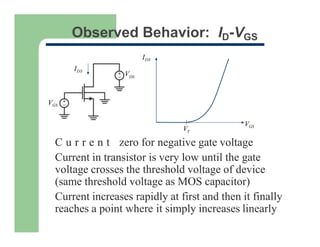
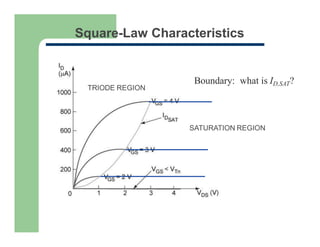
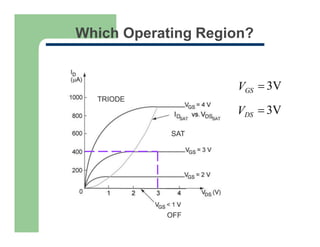
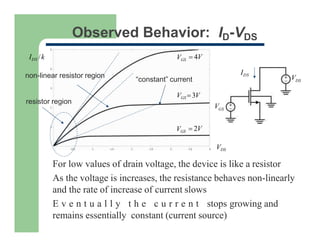
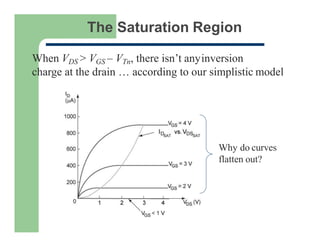
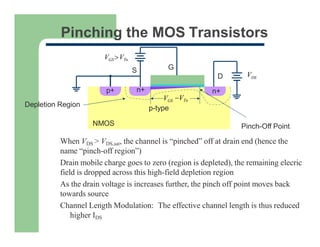
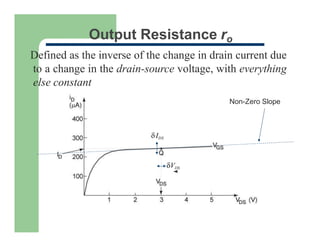
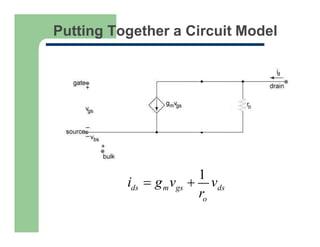
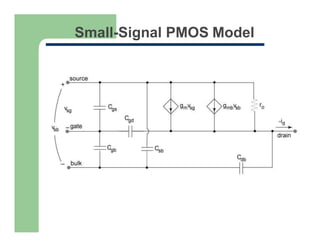
The document discusses MOS transistor models and behavior. It describes: 1) The I-V characteristics of MOS transistors, including the square-law model and linear region behavior as gate voltage exceeds threshold. 2) The saturation region where drain current reaches a maximum and becomes independent of drain-source voltage. 3) The linear small-signal model of the MOSFET as a voltage-controlled resistor with transconductance gm. 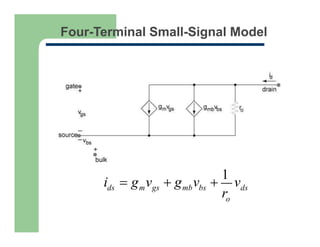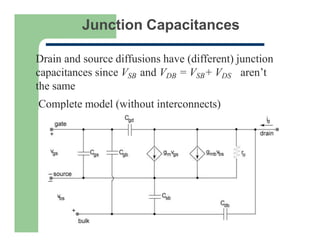4) The development of a four-terminal small-signal model including transconductance gm, output resistance ro, and backgate transconductance gmb.

1. MOS Transistor Models

2. Lecture Outline
MOS Transistors
- I-V curve (Square-Law Model)
– Small Signal Model (Linear Model)

3. Observed Behavior: ID-VGS
C u r r e n t zero for negative gate voltage
Current in transistor is very low until the gate
voltage crosses the threshold voltage of device
(same threshold voltage as MOS capacitor)
Current increases rapidly at first and then it finally
reaches a point where it simply increases linearly
VGS
IDS
T
V
VGS
IDS
DS
V

4. Observed Behavior: ID-VDS
VDS
For low values of drain voltage, the device is like a resistor
As the voltage is increases, the resistance behaves non-linearly
and the rate of increase of current slows
E v e n t u a l l y t h e c u r r e n t stops growing and
remains essentially constant (current source)
IDS /k
“constant” current
resistor region
non-linear resistor region
VGS  2V
VGS  3V
VGS  4V
GS
V
IDS
DS
V

5. “Linear” Region Current
I f t h e gate is biased above threshold, the
surface is inverted
This inverted region forms a channel that connects
the drain and gate
I f a d r a i n voltage is applied positive,
electrons will flow from source to drain
p-type
n+ n+
p+
Inversion layer
“channel”
VGS VTn
DS
V 100mV
G
D
S
NMOS
x
y

6. MOSFET: Variable Resistor
N o t i c e t h a t in the linear region, the
current is proportional to the voltage
Can define a voltage-dependent resistor
T h i s i s a n i c e variable resistor,
electronically tunable!
DS n ox GS Tn DS
L
I 
W
C (V V )V

7. Finding ID = f (VGS, VDS)
Approximate inversion charge QN(y): drain is
higher than the source € less charge at drain end
of channel

8. Inversion Charge at Source/Drain
QN (y)  QN (y  0)  QN (y  L)
QN (y  0)  Cox (VGS VTn ) QN ( y  L)
 Cox (VGD  VTn)
GD  VGS VDS

9. Average Inversion Charge
Charge at drain end is lower since field is lower
Simple approximation: In reality we should
integrate the total charge minus the bulk depletion
charge across the channel
VT )  Cox (VGDVT)
2
N
Q (y)  
Cox (VGS
Source End Drain End
2
N
VT )  Cox (VGSVSD VT )
Q (y)  
Cox (VGS
 2VT) CoxVSD
2 2
N ox GS T
Q (y)  
Cox (2VGS
 C (V V VDS
)

10. Drift Velocity and Drain Current
“Long-channel” assumption: use mobility to find v
n DS
n n V / y) 
v(y)   E(y)   (
Substituting:
L
 V
2
VDS
)
D N ox GS T
L
I  WvQ W
VDS
C (V V
2
D ox GS T DS
L
I 
W
C (V V 
VDS
)V
Inverted Parabolas

11. Square-Law Characteristics
Boundary: what is ID,SAT?
TRIODE REGION
SATURATION REGION

12. The Saturation Region
When VDS > VGS – VTn, there isn’t anyinversion
charge at the drain … according to our simplistic model
Why do curves
flatten out?

13. Square-Law Current in Saturation
Current stays at maximum (where VDS = VGS – VTn =VDS,SAT)
Measurement: ID increases slightly with increasingVDS
model with linear “fudge factor”
2
D ox GS T DS
L
I 
W
C (V V 
VDS
)V
DS,sat
2
ox GS T GS T
VGS VT
)(V V )
L
I 
W
C (V V
DS,sat GS T
L 2
I 
W Cox
(V V )2
2
DS,sat GS T DS
V )
L 2
I 
W Cox
(V V ) (1

14. Pinching the MOS Transistors
When VDS > VDS,sat, the channel is “pinched” off at drain end (hence the
name “pinch-off region”)
Drain mobile charge goes to zero (region is depleted), the remaining elecric
field is dropped across this high-field depletion region
As the drain voltage is increases further, the pinch off point moves back
towards source
Channel Length Modulation: The effective channel length is thus reduced
higher IDS
p-type
n+ n+
p+
Pinch-Off Point
VGS VTn
DS
V
G
D
S
NMOS
Depletion Region
VGS VTn

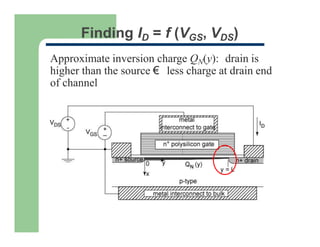
15. Linear MOSFET Model
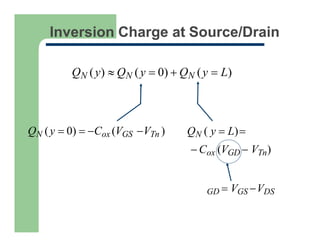
Channel (inversion) charge: neglect reduction at drain
Velocity saturation defines VDS,SAT = Esat L =constant
- vsat /n
Drain current:
ID,SAT  WvQN  W (vsat)[Cox (VGS VTn )],
|Esat| = 104 V/cm, L = 0.12 m € VDS,SAT = 0.12 V!
ID,SAT  vsatWCox (VGS VTn)(1 nVDS )

16. Why Find an Incremental Model?
Direct substitution into iD = f(vGS, vDS) is
tedious AND doesn’t include charge-storage
effects … pretty rough approximation
Signals of interest in analog ICs are often of the
form:
vGS (t)  VGS vgs (t)
Fixed Bias Point Small Signal

17. Which Operating Region?
 3V
 3V
VGS
VDS
TRIODE
SAT
OFF

18. Changing One Variable at a Time
IDS /k
VDS  3V
VT 1V
Square Law
Saturation
Region
Linear
Triode
Region
Slope of Tangent: Incremental current increase
VGS
Assumption: VDS > VDS,SAT = VGS – VTn (square law)

19. The Transconductance gm
Defined as the change in drain current due to a change in the
gate-source voltage, with everything else constant
GS VGS ,VDS

iD
m
GS VGS ,VDS
ox GS T DS
V )(1 V )
g 
iD
v v L
 C
W
(V
2
ox
DS,sat
L 2
GS T DS
V )
(V  V ) (1 
W C
I 
m ox GS T
L
g  C
W
(V V )
 0
m ox ox DS
ox
2IDS
W
L
W
I
L
 2C
g  C
L
W
C
2IDS
(VGS VT )
m
g 
Gate Bias
Drain Current Bias
Drain Current Bias and
Gate Bias

20. Output Resistance ro
Defined as the inverse of the change in drain current due
to a change in the drain-source voltage, with everything
else constant
Non-Zero Slope
VDS
IDS

21. Evaluating ro
o
DS
iD

r 
1
v VGS ,VDS
2
ox
L 2
D GS T DS
V )
(V V ) (1 
W C
i 
0
2
1
ox
(VGS
L 2 T
V ) 
r 
W C
0
1
DS
r 
I

22. Total Small Signal Current
iDS (t)  IDS ids

iDS  iDS
v
ds gs ds
gs ds
i v
v v
ds m gs ds
o
r
i  g v 
1
v
Transconductance
Conductance

23. Putting Together a Circuit Model
ds m gs ds
o
i
r
 g v 
1
v

24. Role of the Substrate Potential
Need not be the source potential, but VB <VS
Effect: changes threshold voltage, which
changes the drain current … substrate acts
like a “backgate”
vBS Q

iD
vBS Q
gmb 
iD
Q = (VGS, VDS, VBS)

25. Backgate Transconductance
Result:  gm
mb
BS BS
Tn Q
VTn

iD
BS p
2 V 2
Q Q
g 
iD
v V v

VSB  2p
VT  VT0    2p 

26. Four-Terminal Small-Signal Model
ds m gs mb bs ds
o
i  g v
r
 g v 
1
v

27. MOSFET Capacitances in Saturation
Gate-source capacitance: channel charge is not
controlled by drain in saturation.

28. Gate-Source Capacitance Cgs
Wedge-shaped charge in saturation € effective area is (2/3)WL
(see H&S 4.5.4 for details)
Cgs  (2/3)WLCox  Cov
Overlap capacitance along source edge of gate €
Cov  LDWCox
(Underestimate due to fringing fields)

29. Gate-Drain Capacitance Cgd
Not due to change in inversion charge in channel
Overlap capacitance Cov between drain and source
is Cgd

30. Junction Capacitances
Drain and source diffusions have (different) junction
capacitances since VSB and VDB = VSB+ VDS aren’t
the same
Complete model (without interconnects)

31. P-Channel MOSFET
Measurement of –IDp versus VSD, with VSG as a parameter:

32. Square-Law PMOS Characteristics

33. Small-Signal PMOS Model

34. MOSFET SPICE Model
Many “levels” … we will use the square-law
“Level 1” model
See H&S 4.6 + Spice refs. on reserve for details.