MOSFET operation characteristics and types

Substrate
Channel Drain
Insulator
Gate
Operation of a transistor
VSG > 0
n type operation
Positive gate bias attracts electrons into channel
Channel now becomes more conductive
More
electrons
Source
VSD
VSG

Some important equations in the
inversion regime (Depth direction)
VT = ms + 2B + ox
Wdm = [2S(2B)/qNA]
Qinv = -Cox(VG - VT)
ox = Qs/Cox
Qs = qNAWdm
VT = ms + 2B + [4SBqNA]/Cox
Substrate
Channel Drain
Insulator
Gate
Source
x

MOSFET Geometry
x
y
z
L
Z
S D
VG
VD

How to include y-dependent potential
without doing the whole problem over?

Assume potential V(y) varies slowly along
channel, so the x-dependent and y-dependent
electrostats are independent
(GRADUAL CHANNEL APPROXIMATION)
i.e.,
Ignore ∂Ex/∂y
Potential is separable in
x and y

How to include y-dependent potentials?
S = 2B + V(y)
VG = S + [2SSqNA]/Cox
Need VG – V(y) > VT to invert
channel at y (V increases
threshold)
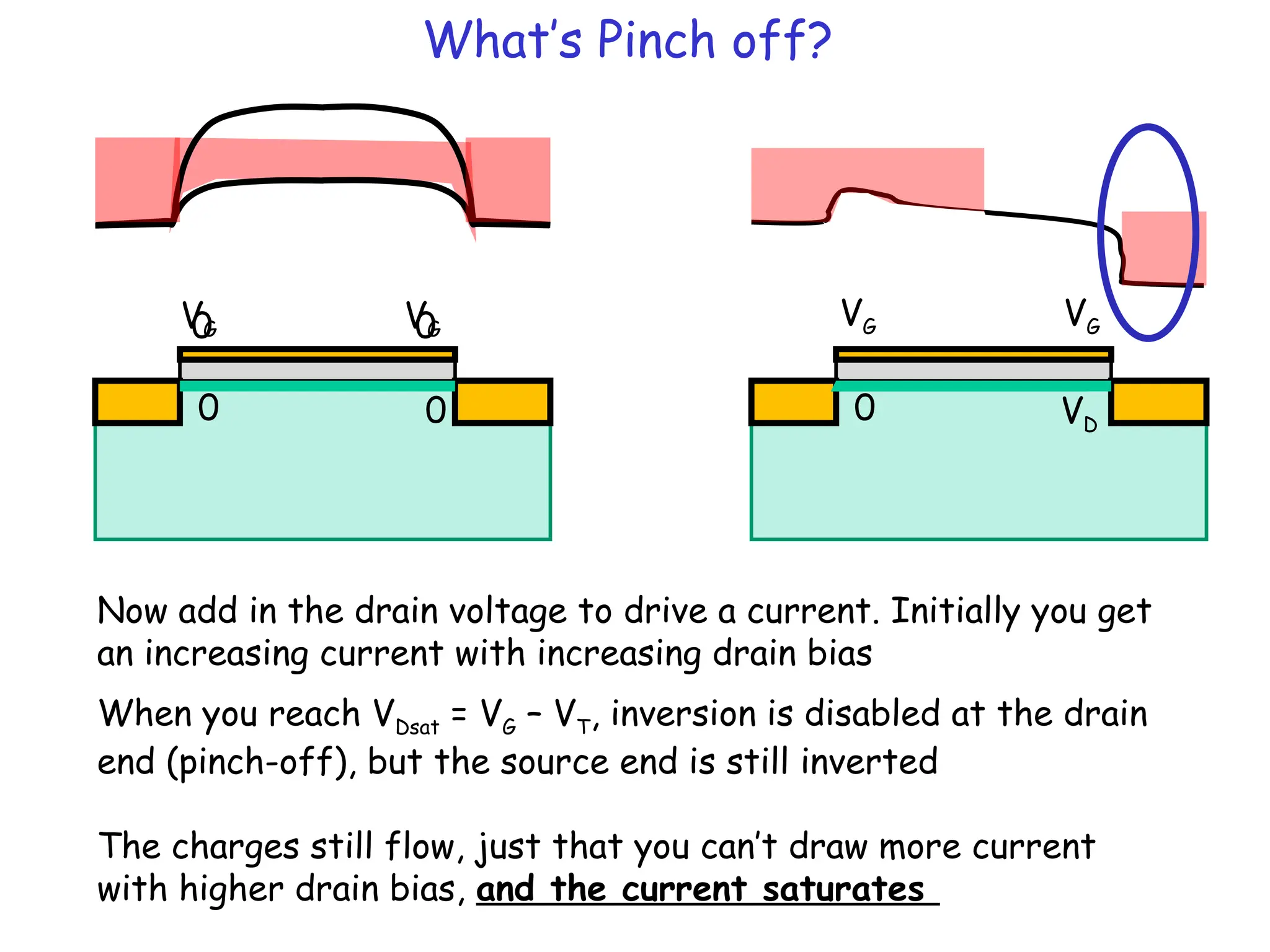
Since V(y) largest at drain end, that
end reverts from inversion to
depletion first (Pinch off) 
SATURATION [VDSAT = VG – VT]

j = qninvv = (Qinv/tinv)v
I = jA = jZtinv = ZQinvv
So current:
Qinv = -Cox[VG – VT - V(y)]
v = -effdV(y)/dy

So current:
I = eff ZCox[VG – VT - V(y)]dV(y)/dy
I = eff ZCox[(VG – VT )VD- VD
2
/2]/L
Continuity implies ∫Idy = IL

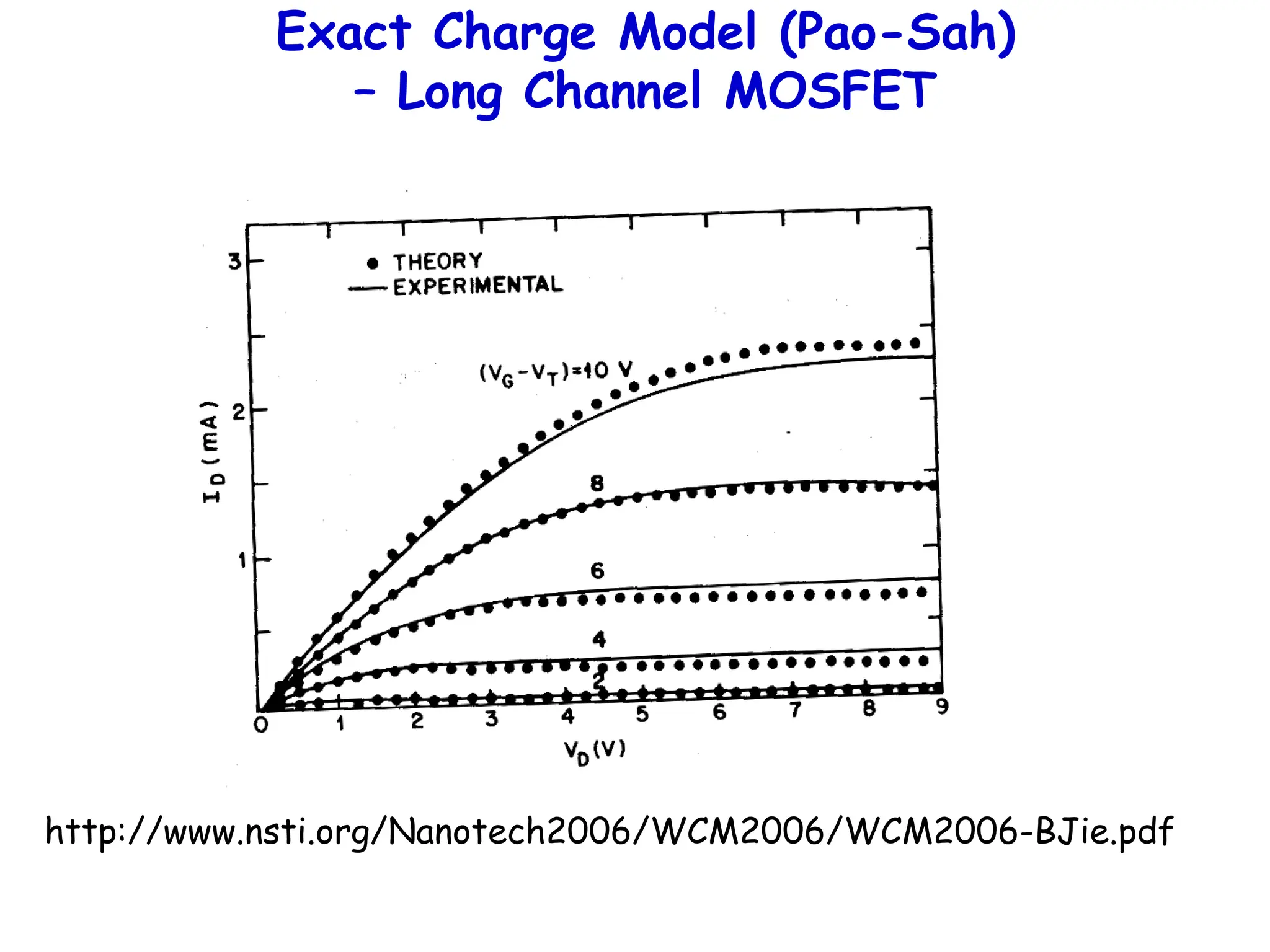
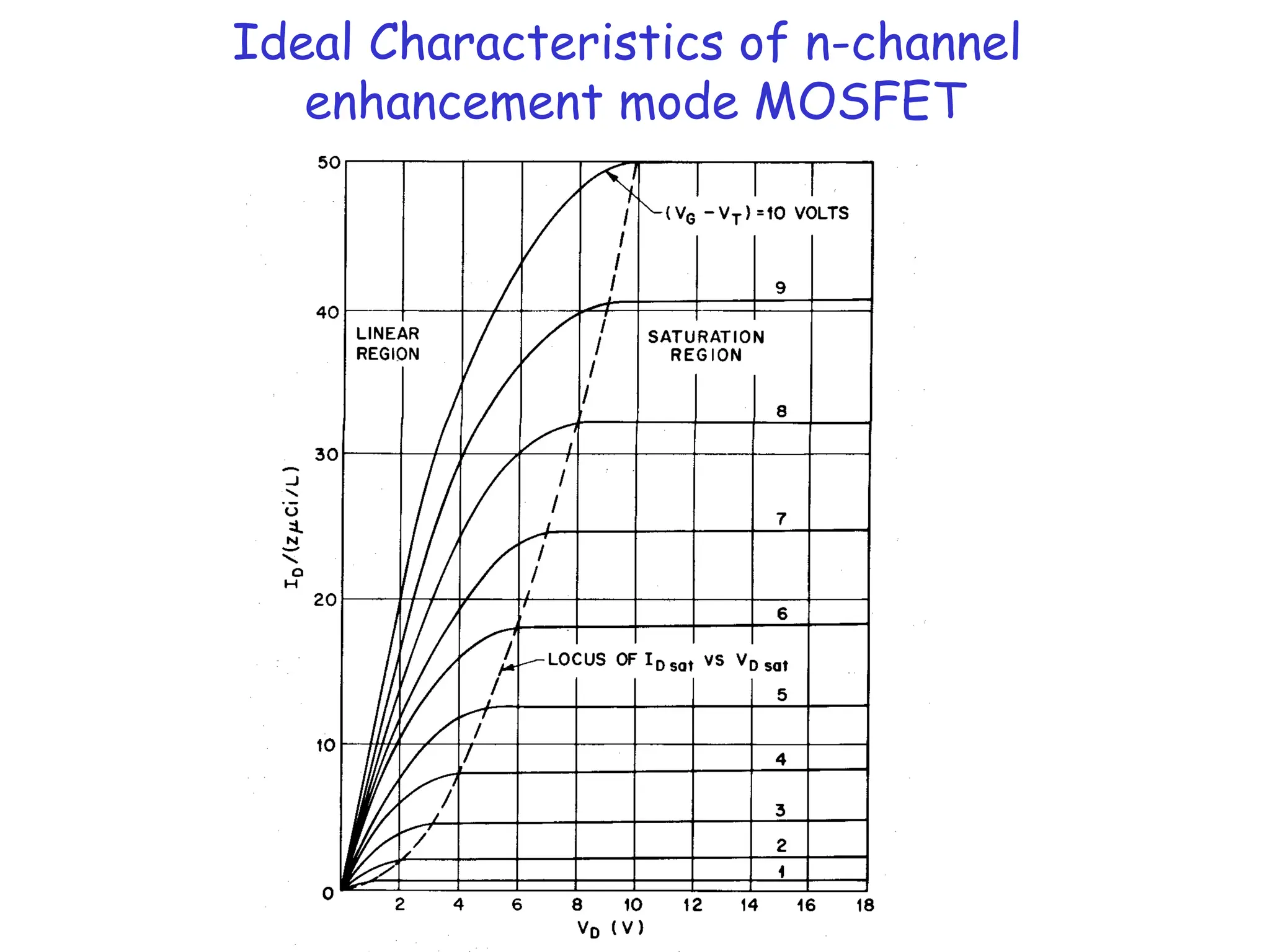
But this current behaves like a parabola !!
ID
VD
IDsat
VDsat
2
/2]/L
We have assumed inversion in our model (ie, always above pinch-off)
So we just extend the maximum current into saturation…
Easy to check that above current is maximum for VDsat = VG - VT
Substituting, IDsat = (CoxeffZ/2L)(VG-VT)2

What’s Pinch off?
0
0 0
0
VG VG
Now add in the drain voltage to drive a current. Initially you get
an increasing current with increasing drain bias
0 VD
VG VG
When you reach VDsat = VG – VT, inversion is disabled at the drain
end (pinch-off), but the source end is still inverted
The charges still flow, just that you can’t draw more current
with higher drain bias, and the current saturates

Square law theory of MOSFETs
2
/2]/L, VD < VG - VT
I = eff ZCox(VG – VT )2
/2L, VD > VG - VT
J = qnv
n ~ Cox(VG – VT )
v ~ effVD /L
NEW

Ideal Characteristics of n-channel
enhancement mode MOSFET

Drain current for REALLY small VD
 
 
 
 
T
G
D
D
T
G
i
n
D
D
D
T
G
i
n
D
V
V
V
V
V
V
C
L
Z
I
V
V
V
V
C
L
Z
I















2
2
1
Linear operation
Channel Conductance:
)
( T
G
i
n
V
D
D
D V
V
C
L
Z
V
I
g
G






Transconductance:
D
i
n
V
G
D
m V
C
L
Z
V
I
g
D






In Saturation
• Channel Conductance:
• Transconductance:
 2
2
T
G
i
n
D V
V
C
L
Z
sat
I 


0




G
V
D
D
D
V
I
g
 
T
G
i
n
V
G
D
m V
V
C
L
Z
V
I
g
D







Equivalent Circuit – Low Frequency AC
• Gate looks like open circuit
• S-D output stage looks like current source with channel
conductance
g
m
d
D
G
V
G
D
D
V
D
D
D
v
g
v
g
i
V
V
I
V
V
I
I
D
G












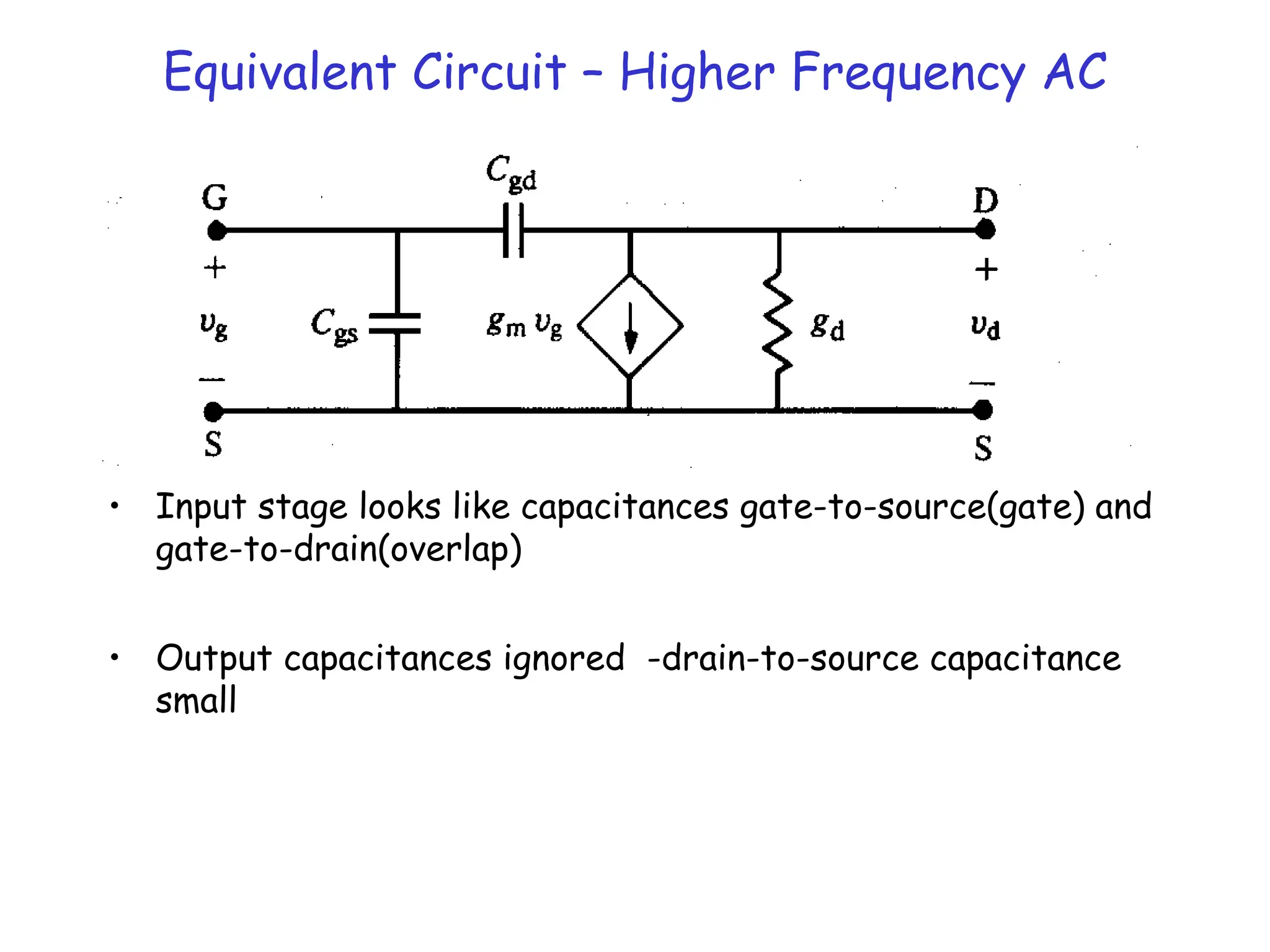
• Input stage looks like capacitances gate-to-source(gate) and
gate-to-drain(overlap)
• Output capacitances ignored -drain-to-source capacitance
small
Equivalent Circuit – Higher Frequency AC

• Input circuit:
• Input capacitance is mainly gate capacitance
• Output circuit:
  g
gate
g
gd
gs
in v
fC
j
v
C
C
j
i 



 2
g
m
out v
g
i 
gate
m
in
out
fC
g
i
i


2
D
i
n
V
G
D
m V
C
L
Z
V
I
g
D





Equivalent Circuit – Higher Frequency AC

Maximum Frequency (not in saturation)
• Ci is capacitance per unit area and Cgate is total capacitance
of the gate
• F=fmax when gain=1 (iout/iin=1)
2
max
max
2
2
2
L
V
ZL
C
C
V
L
Z
f
C
g
f
D
n
i
i
D
n
gate
m








ZL
C
C i
gate 

Maximum Frequency (not in saturation)
2
max 2 L
V
f D
n



L
V
v
v
L
D /
/
1
max




(Inverse transit time)
NEW

Switching Speed, Power Dissipation
ton = CoxZLVD/ION
Trade-off: If Cox too small, Cs and Cd take over and you lose
control of the channel potential (e.g. saturation)
(DRAIN-INDUCED BARRIER LOWERING/DIBL)
If Cox increases, you want to make sure you don’t control
immobile charges (parasitics) which do not contribute to
current.

Switching Speed, Power Dissipation
Pdyn = ½ CoxZLVD
2
f
Pst = IoffVD

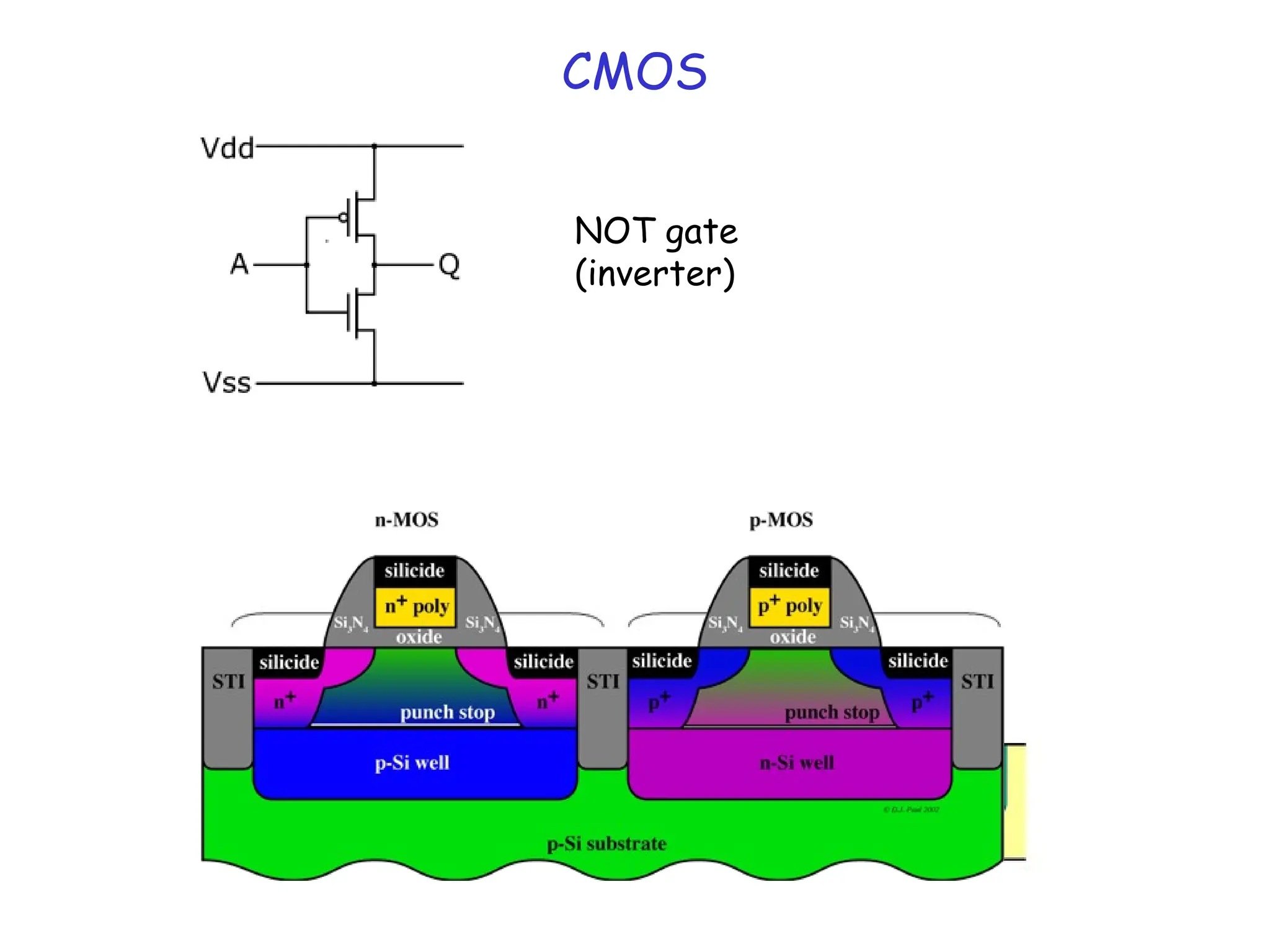
CMOS
NOT gate
(inverter)
Positive gate turns nMOS on
Vin = 1 Vout = 0

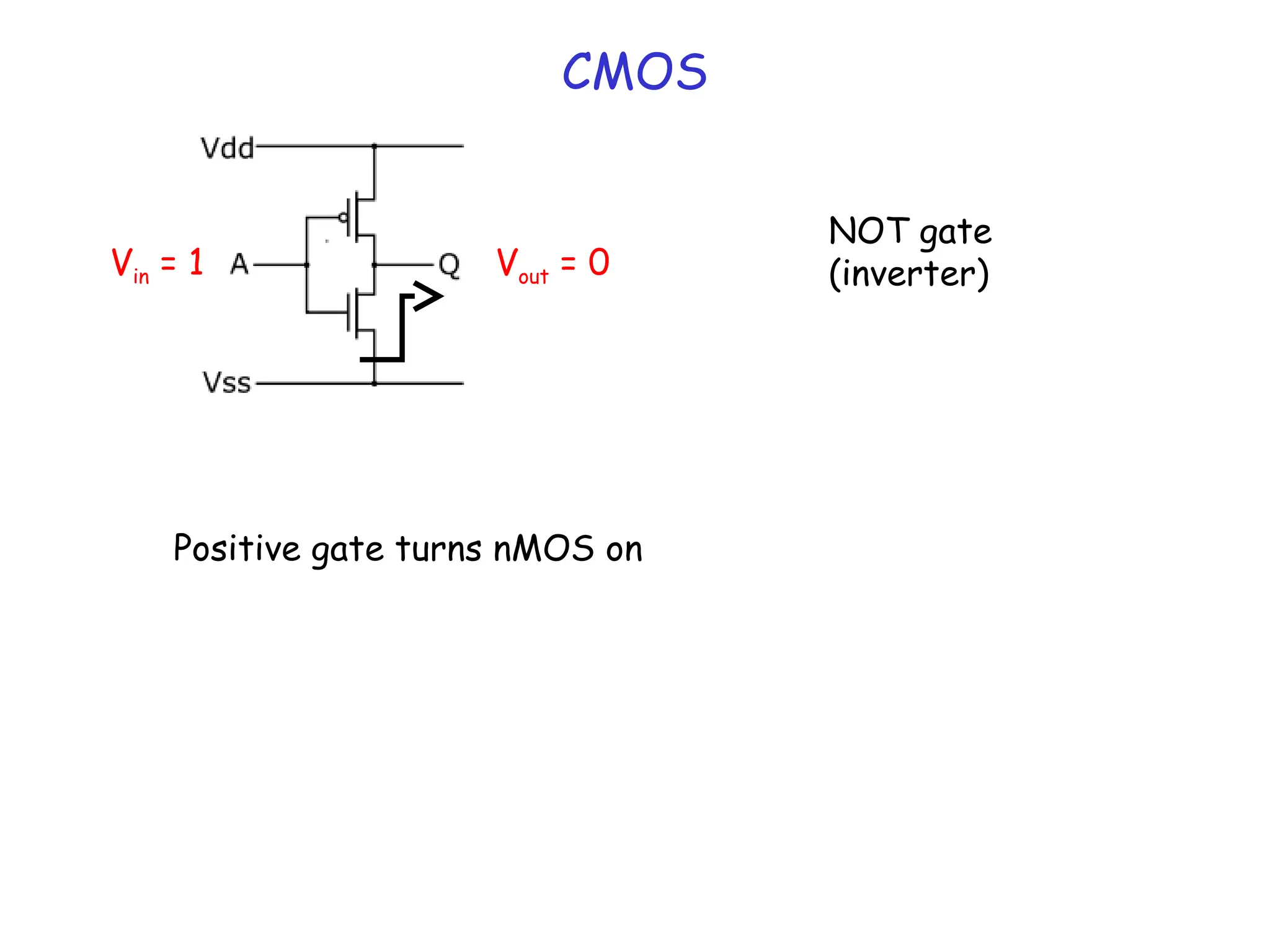
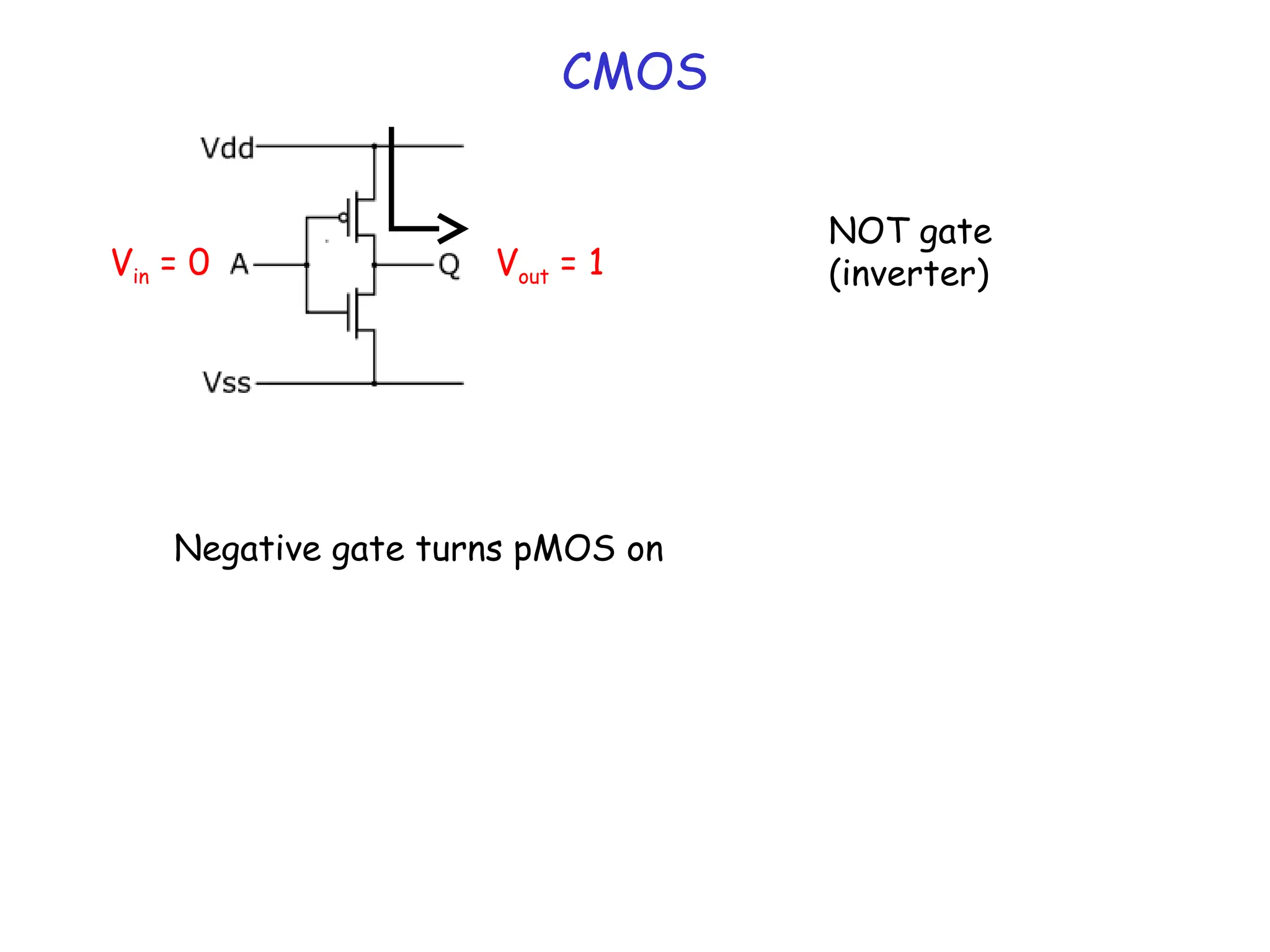
CMOS
NOT gate
(inverter)
Negative gate turns pMOS on
Vin = 0 Vout = 1

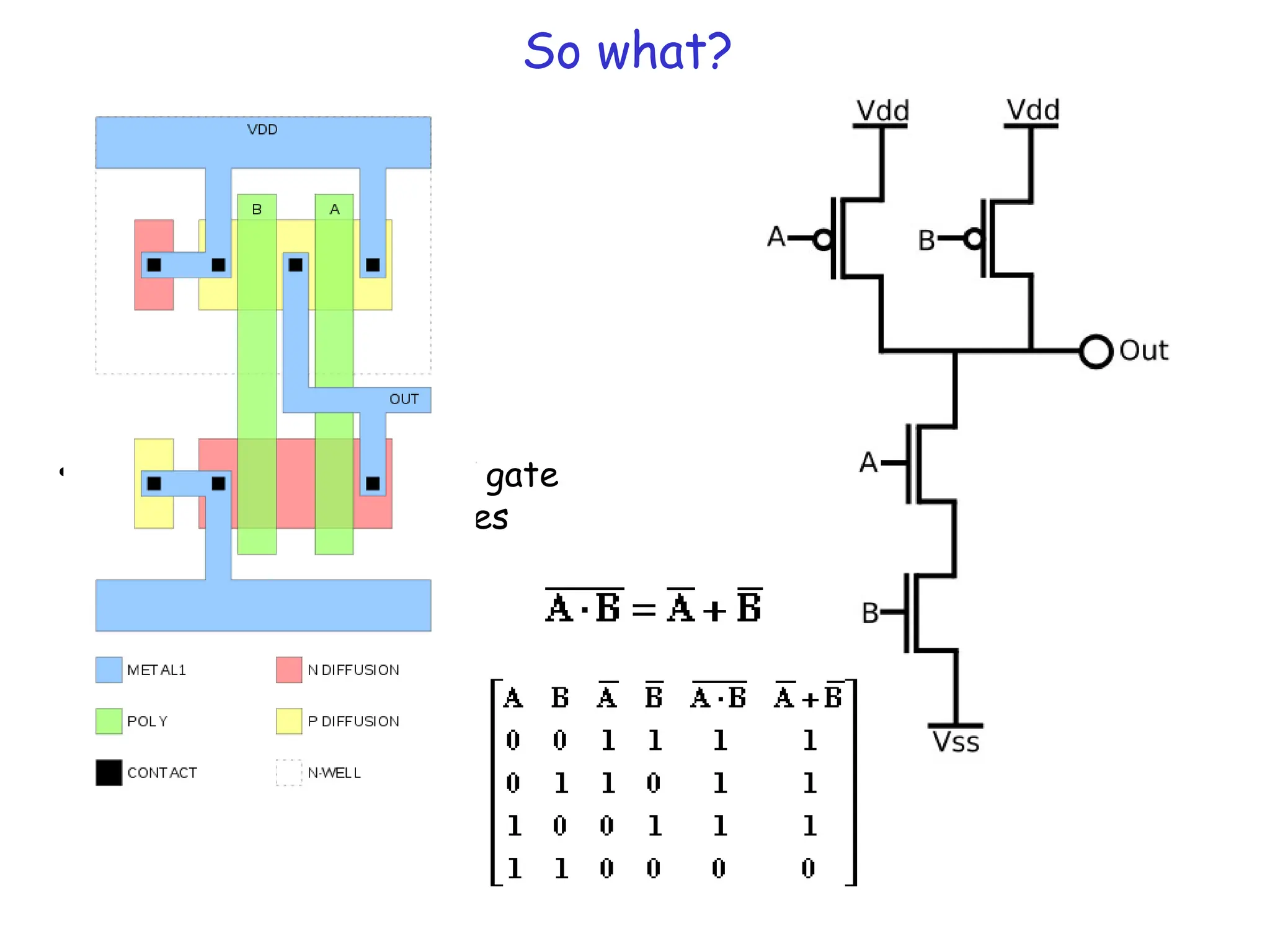
So what?
• If we can create a NOT gate
we can create other gates
(e.g. NAND, EXOR)

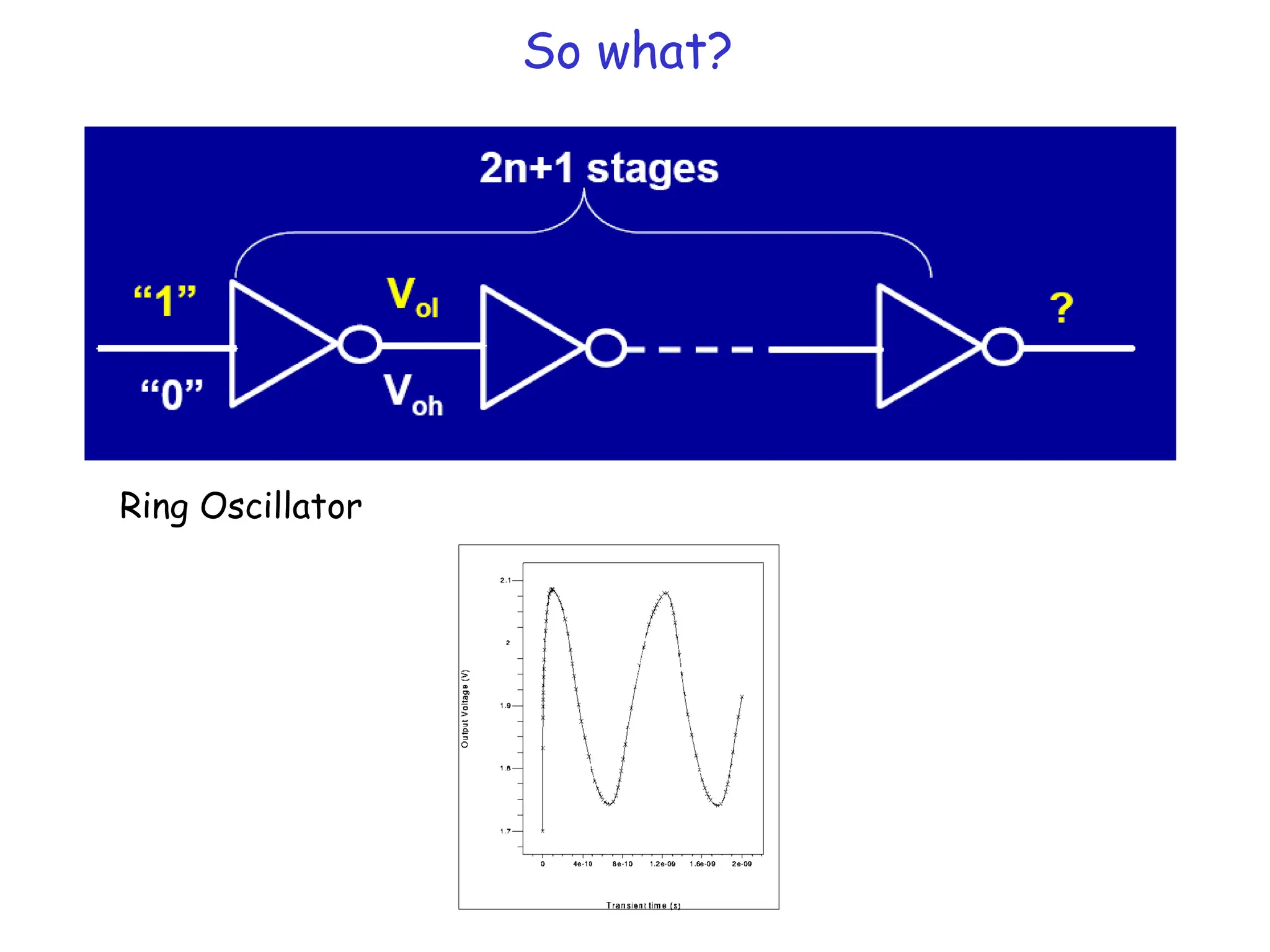
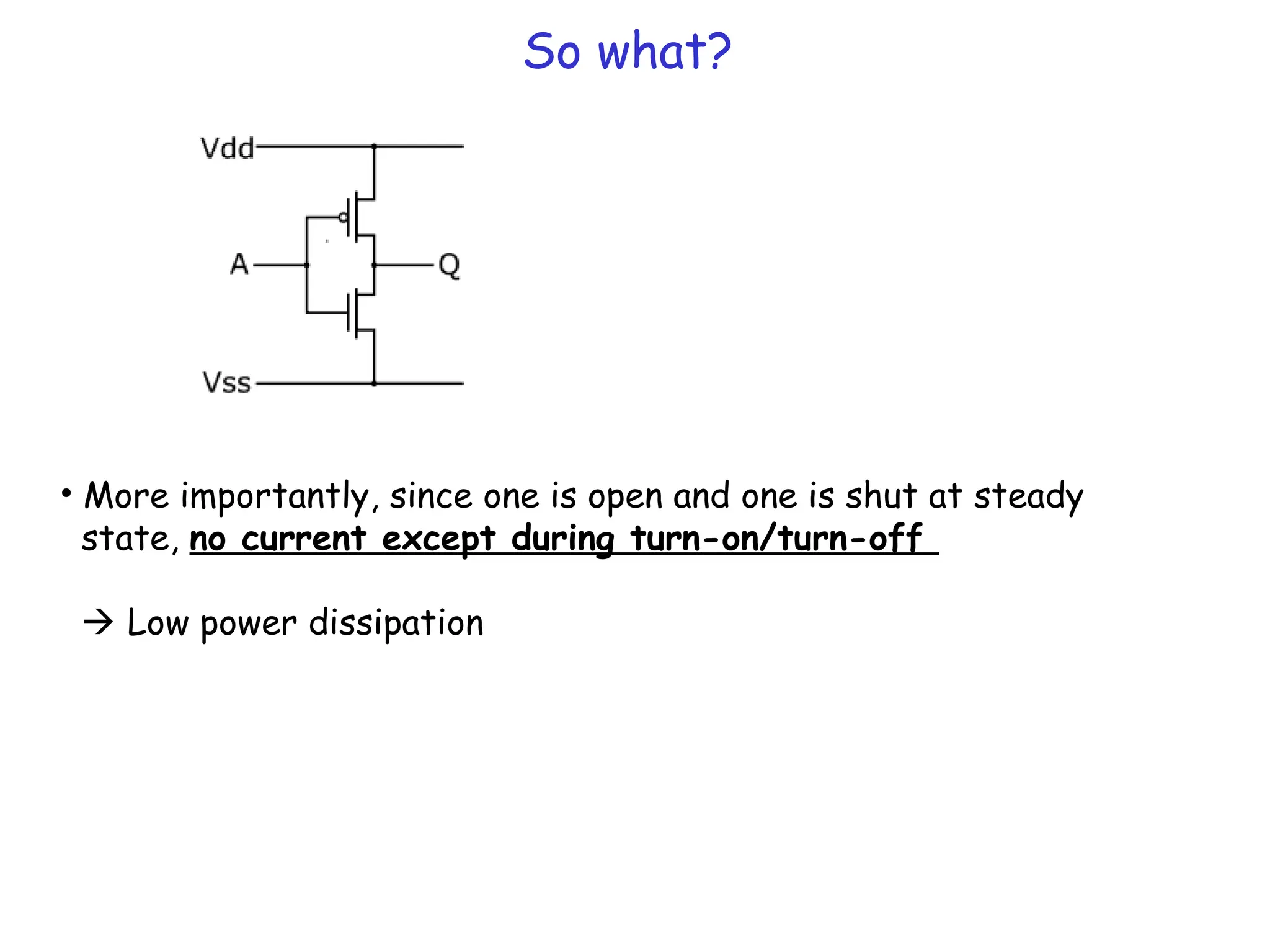
So what?
• More importantly, since one is open and one is shut at steady
state, no current except during turn-on/turn-off
 Low power dissipation

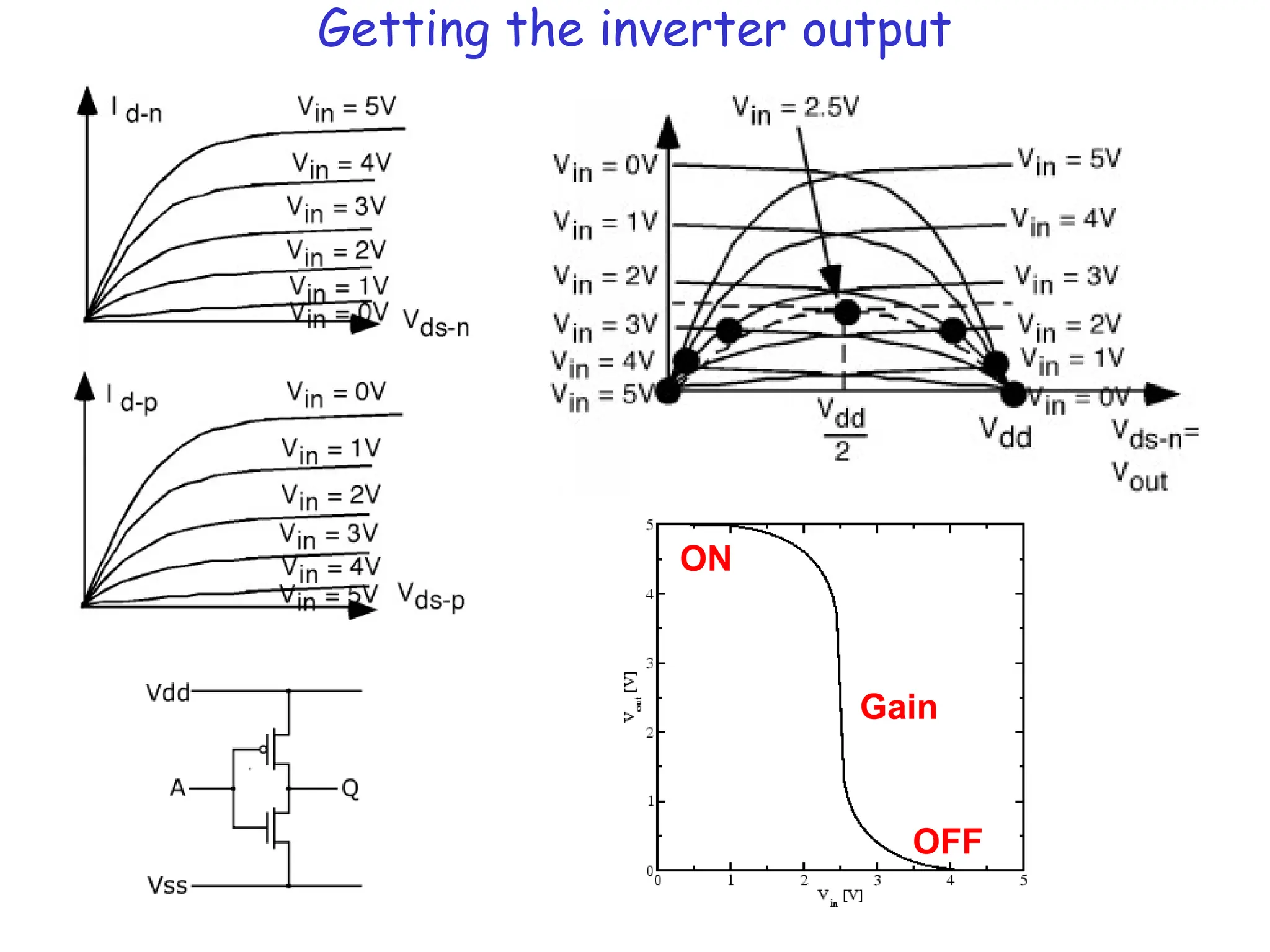
Getting the inverter output
Gain
ON
OFF

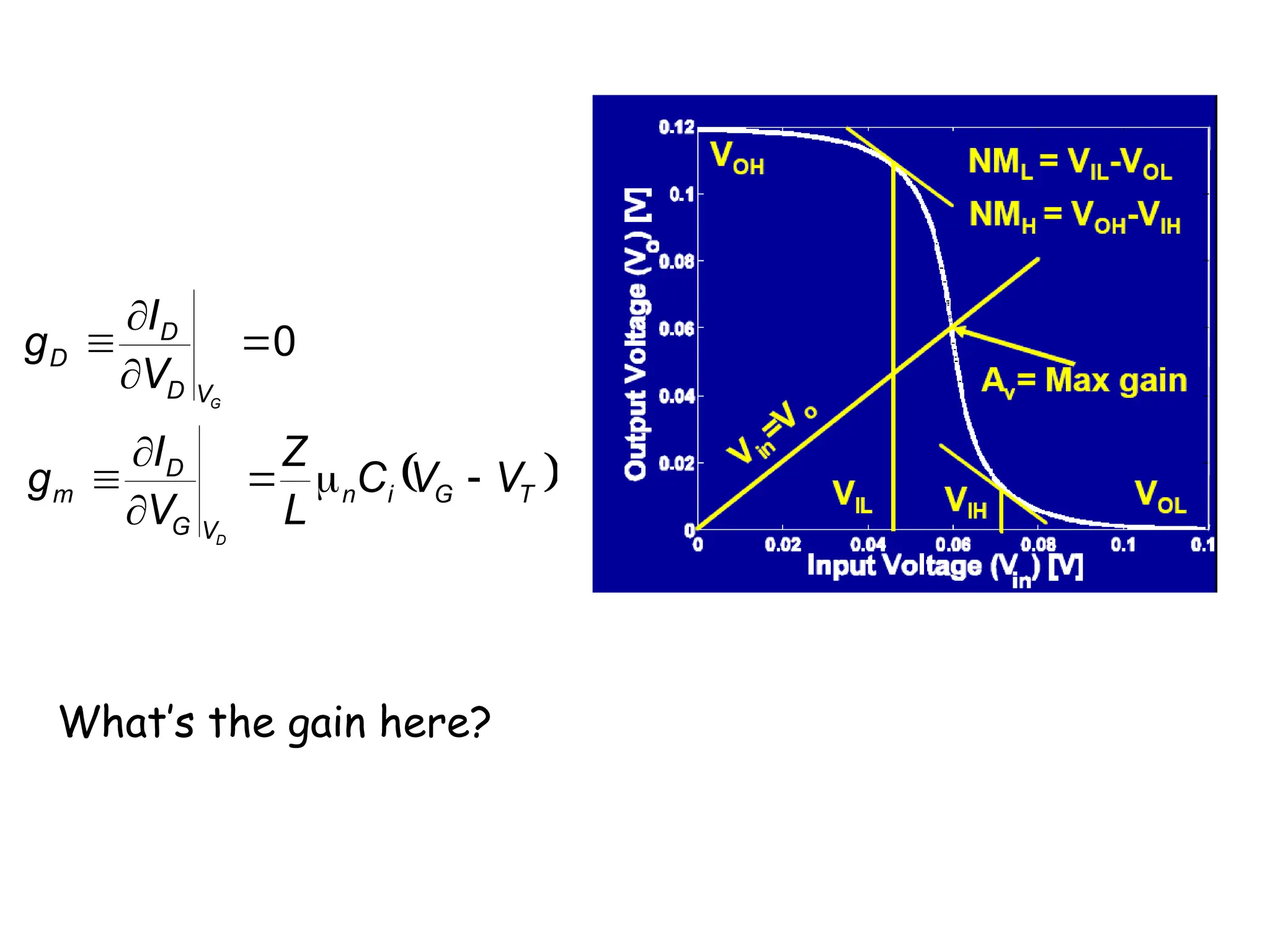
0




G
V
D
D
D
V
I
g
 
T
G
i
n
V
G
D
m V
V
C
L
Z
V
I
g
D






What’s the gain here?

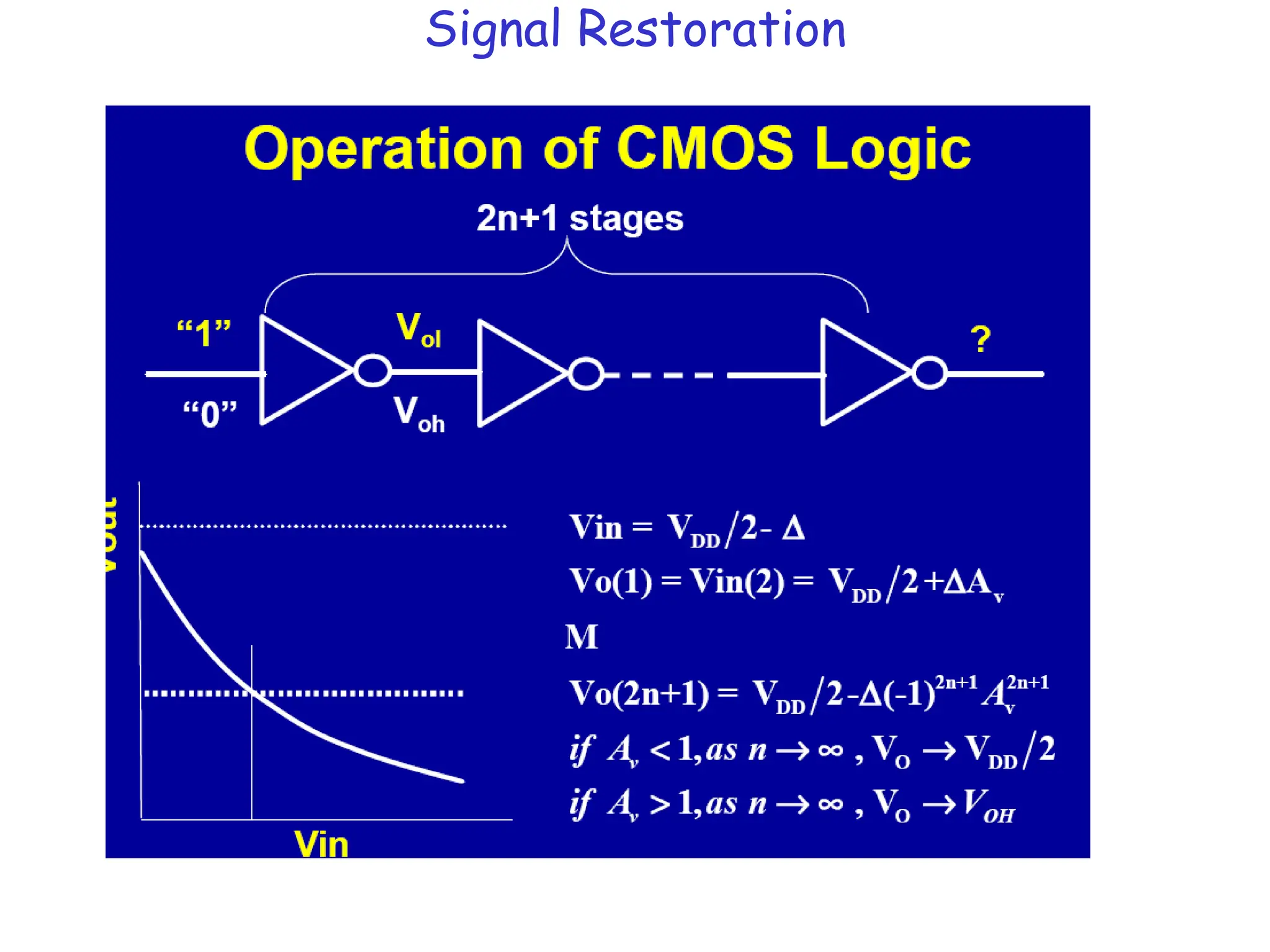
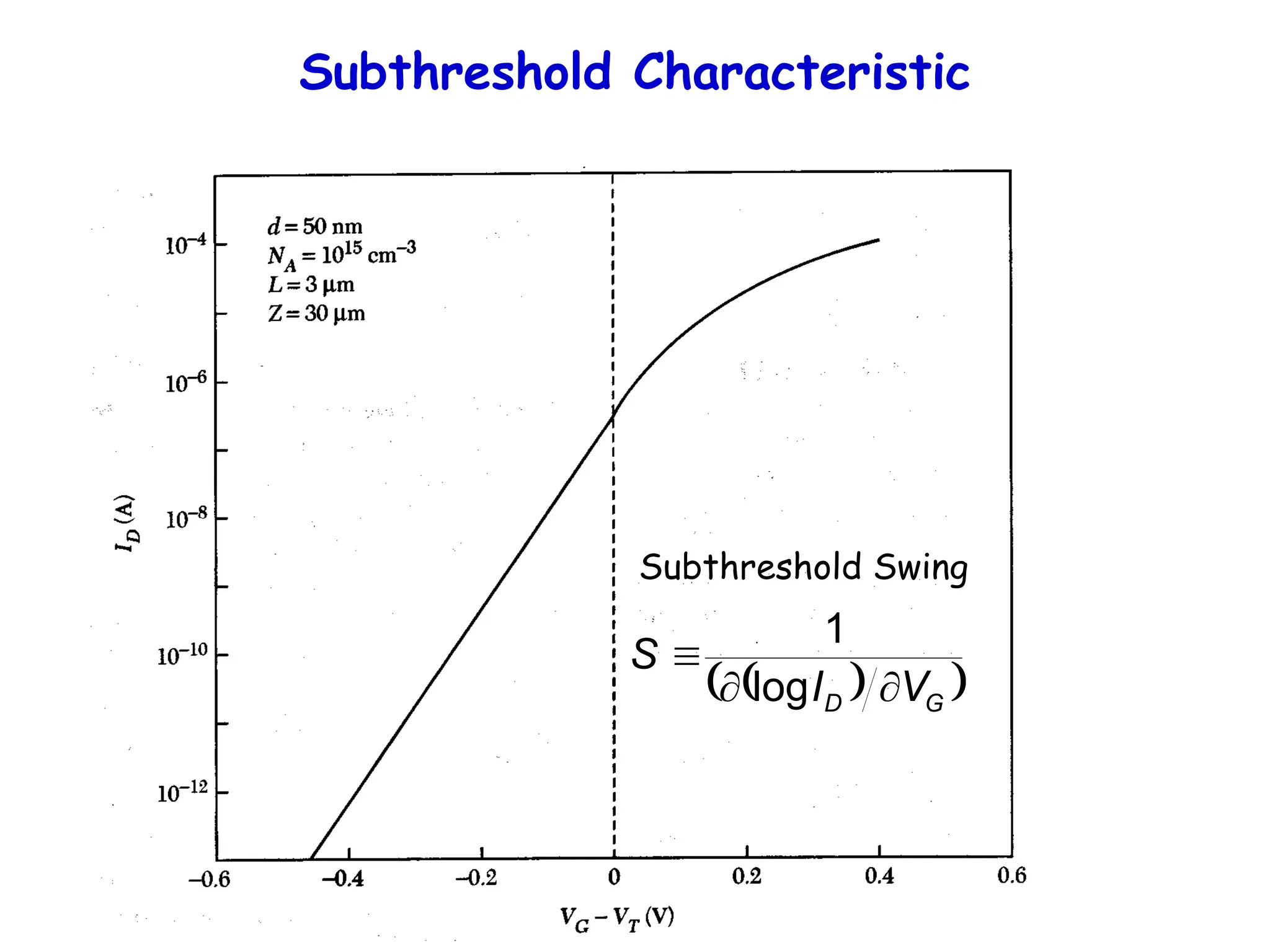
BJT vs MOSFET
• RTL logic vs CMOS logic
• DC Input impedance of MOSFET (at gate end) is infinite
Thus, current output can drive many inputs  FANOUT
• CMOS static dissipation is low!! ~ IOFFVDD
• Normally BJTs have higher transconductance/current (faster!)
IC = (qni
2
Dn/WBND)exp(qVBE/kT) ID = CoxW(VG-VT) 2
/L
gm = IC/VBE = IC/(kT/q) gm = ID/VG = ID/[(VG-VT)/2]
• Today’s MOSFET ID >> IC due to near ballistic operation
NEW

What if it isn’t ideal?
• If work function differences and oxide charges are present,
threshold voltage is shifted just like for MOS capacitor:
• If the substrate is biased wrt the Source (VBS) the
threshold voltage is also shifted
i
B
A
s
B
i
f
ms
i
B
A
s
B
FB
T
C
qN
C
Q
C
qN
V
V
)
2
(
2
2
)
2
(
2
2




















i
BS
B
A
s
B
FB
T
C
V
qN
V
V
)
2
(
2
2








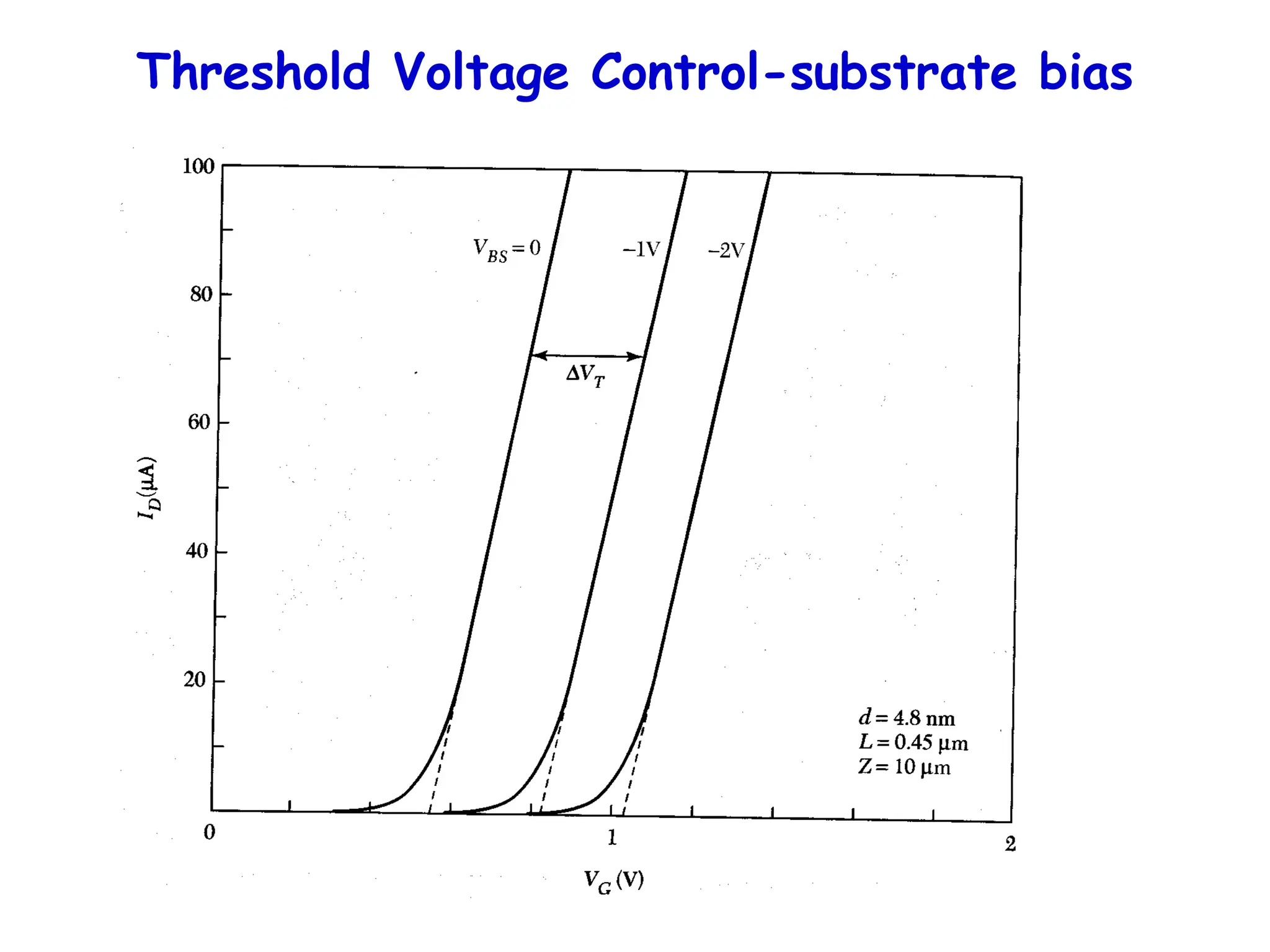
Threshold Voltage Control
• Substrate Bias:
i
BS
B
A
s
B
FB
T
C
V
qN
V
V
)
2
(
2
2







 
B
BS
B
i
A
s
T
BS
T
BS
T
T
V
C
qN
V
V
V
V
V
V











2
2
2
)
0
(
)
(

Threshold Voltage Control-substrate bias

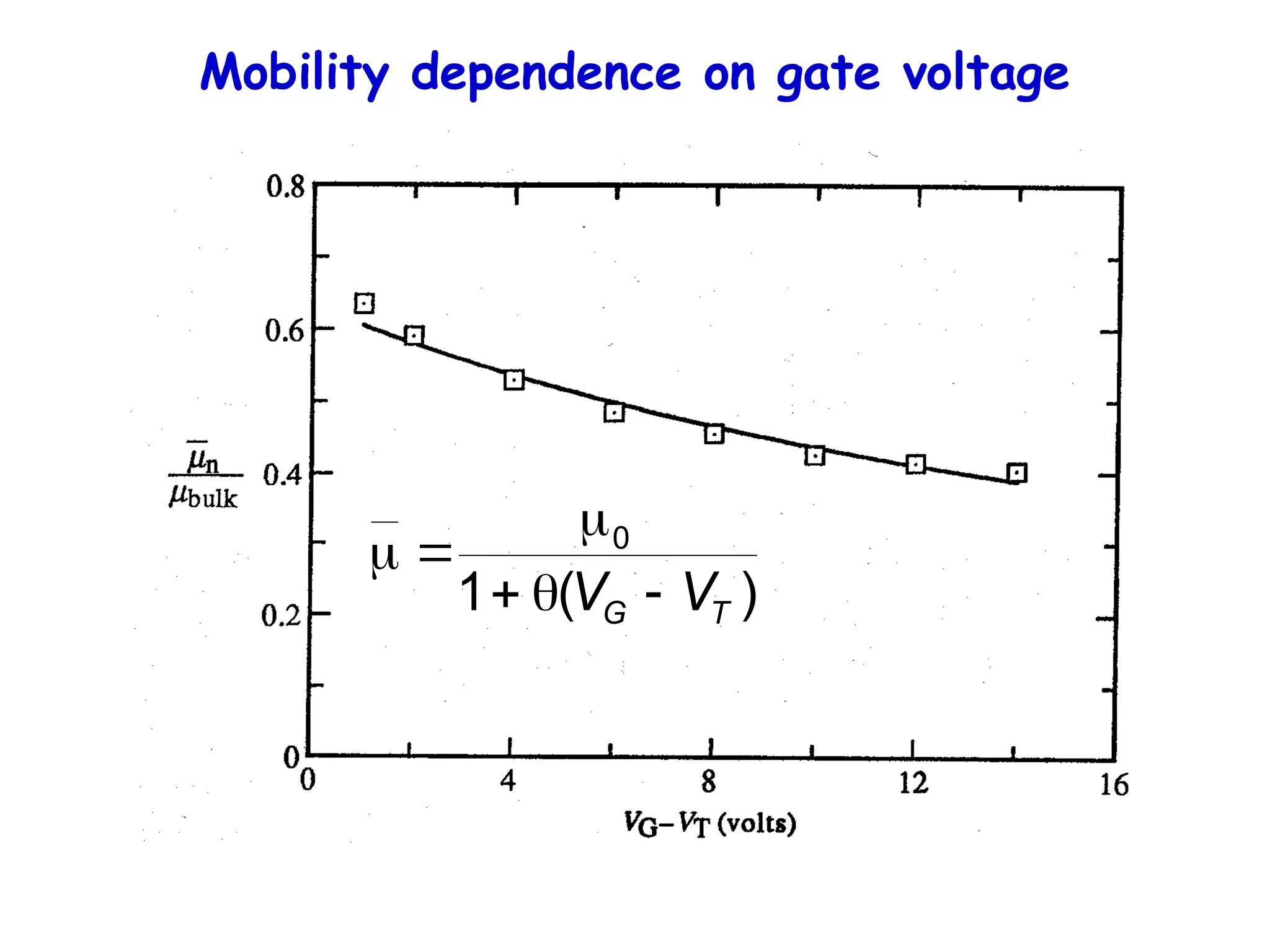
It also affects the I-V
VG
The threshold voltage is increased due to the depletion region
that grows at the drain end because the inversion layer shrinks
there and can’t screen it any more. (Wd > Wdm)
Qinv = -Cox[VG-VT(y)], I = -effZQinvdV(y)/dy
VT(y) =  + √2sqNA/Cox
 = 2B + V(y)

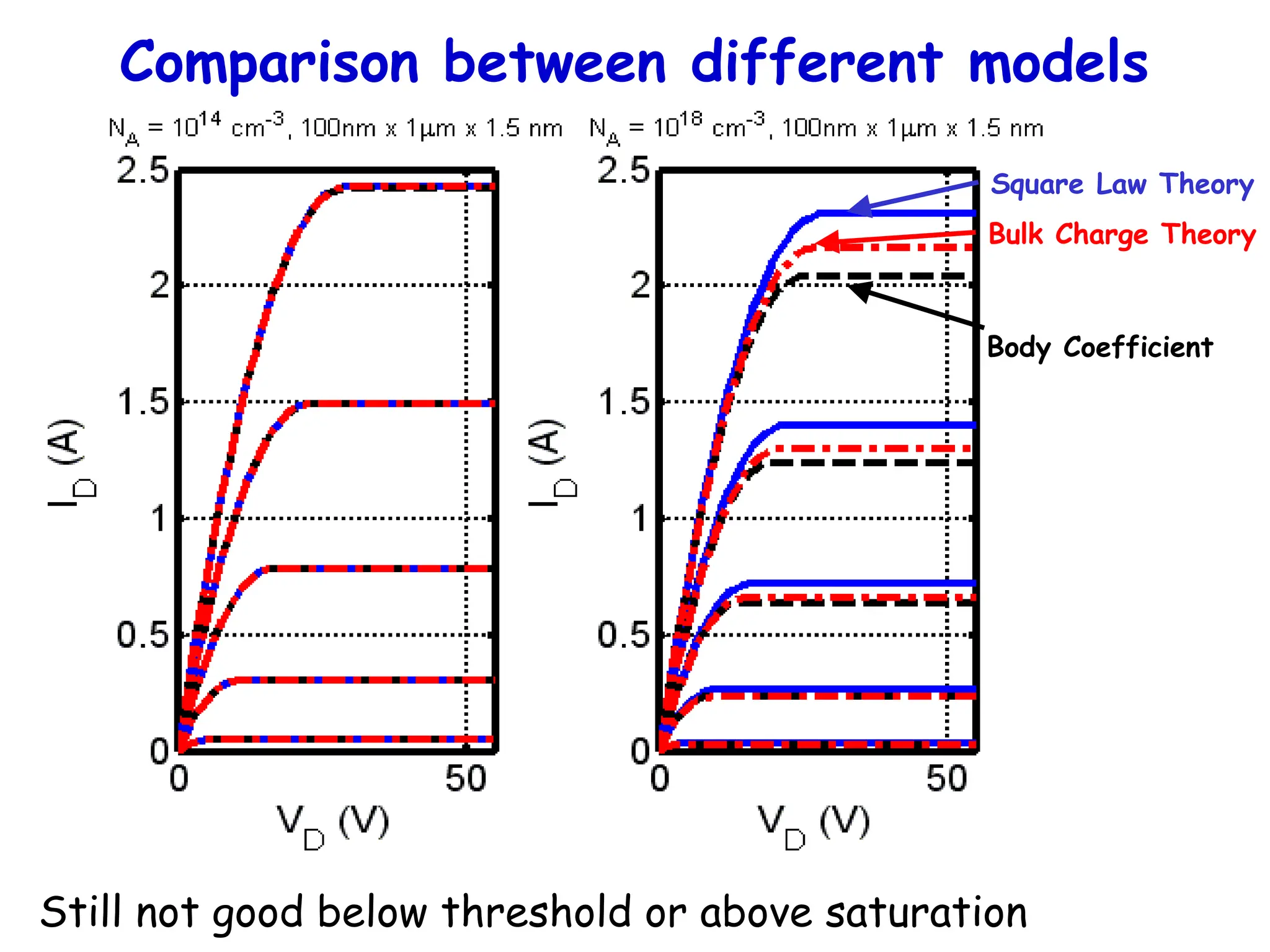
It also affects the I-V
IL = ∫effZCox[VG – (2B+V) - √2sqNA(2B+V)/Cox]dV
I = (ZeffCox/L)[(VG–2B)VD –VD
2
/2
-2√2sqNA{(2B+VD)3/2
-(2B)3/2
}/3Cox]

We can approximately include this…
Include an additional charge term from the
depletion layer capacitance controlling V(y)
Q = -Cox[VG-VT]+(Cox + Cd)V(y)
where Cd = s/Wdm
Q = -Cox[VG –VT - MV(y)], M = 1 + Cd/Cox
ID = (ZeffCox/L)[(VG-VT - MVD/2)VD]

Comparison between different models
Square Law Theory
Body Coefficient
Bulk Charge Theory
Still not good below threshold or above saturation

Mobility
• Drain current model assumed constant mobility in channel
• Mobility of channel less than bulk – surface scattering
• Mobility depends on gate voltage – carriers in inversion
channel are attracted to gate – increased surface scattering
– reduced mobility

Mobility dependence on gate voltage
)
(
1
0
T
G V
V 






Sub-Threshold Behavior
• For gate voltage less than the threshold – weak inversion
• Diffusion is dominant current mechanism (not drift)
L
L
n
o
n
qAD
y
n
qAD
A
J
I n
n
D
D
)
(
)
( 







kT
V
q
i
kT
q
i
D
B
s
B
s
e
n
L
n
e
n
n
/
)
(
/
)
(
)
(
)
0
(










Sub-threshold
  kT
q
kT
qV
kT
i
n
D
s
D
B
e
e
L
e
n
qAD
I /
/
/
1 





We can approximate s with VG-VT below threshold since all
voltage drops across depletion region
    kT
V
V
q
kT
qV
kT
i
n
D
T
G
D
B
e
e
L
e
n
qAD
I /
/
/
1 





•Sub-threshold current is exponential function of applied gate voltage
•Sub-threshold current gets larger for smaller gates (L)

Subthreshold Characteristic
 
 
G
D V
I
S



log
1
Subthreshold Swing

Tunneling transistor
– Band filter like operation
J Appenzeller et al, PRL ‘04
Ghosh, Rakshit, Datta
(Nanoletters, 2004)
(Sconf)min=2.3(kBT/e).(etox/m)
Hodgkin and Huxley, J. Physiol. 116, 449 (1952a)
Subthreshold slope = (60/Z) mV/decade
Much of new research depends on reducing S !

Much of new research depends on reducing S !
• Increase ‘q’ by collective motion (e.g. relay)
Ghosh, Rakshit, Datta, NL ‘03
• Effectively reduce N through interactions
Salahuddin, Datta
• Negative capacitance
Salahuddin, Datta
• Non-thermionic switching (T-independent)
Appenzeller et al, PRL
• Nonequilibrium switching
Li, Ghosh, Stan
• Impact Ionization
Plummer

More complete model – sub-threshold to
saturation
• Must include diffusion and drift currents
• Still use gradual channel approximation
• Yields sub-threshold and saturation behavior for long
channel MOSFETS
• Exact Charge Model – numerical integration


















D s
B
V
p
p
V
D
n
s
D
p
n
V
F
e
L
L
Z
I
0
0
0
,
,

Exact Charge Model (Pao-Sah)
– Long Channel MOSFET
http://www.nsti.org/Nanotech2006/WCM2006/WCM2006-BJie.pdf

MOSFET operation characteristics and types

MOSFET operation characteristics and types

More Related Content

Similar to MOSFET operation characteristics and types

Recently uploaded

MOSFET operation characteristics and types