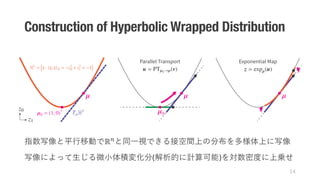
1. The document presents a novel hyperbolic distribution called the pseudo-hyperbolic Gaussian, which is a Gaussian distribution on hyperbolic space that can be evaluated analytically and differentiated with respect to parameters. 2. This distribution enables gradient-based learning of probabilistic models on hyperbolic space. It also allows sampling from the hyperbolic probability distribution without auxiliary means like rejection sampling. 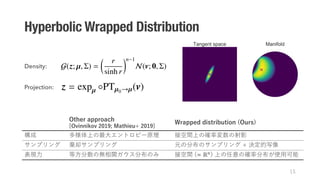3. As applications of the distribution, the authors develop a hyperbolic variational autoencoder and a method for probabilistic word embedding on hyperbolic space. They demonstrate the efficacy of the distribution on datasets including MNIST, Atari 2600 Breakout, and WordNet.

1. A Wrapped Normal Distribution on Hyperbolic Space
for Gradient Based Learning
ICML’19, Jun 12th, 2019
Yoshihiro Nagano1), Shoichiro Yamaguchi2), Yasuhiro Fujita2), Masanori Koyama2)
1) Department of Complexity Science, The University of Tokyo, Japan
2) Preferred Networks, Inc., Japan
Paper: proceedings.mlr.press/v97/nagano19a.html
Code: github.com/pfnet-research/hyperbolic_wrapped_distribution
ICLR/ICML2019 , Jul 21st, 2019

2. Yoshihiro Nagano
2017-Current Ph.D. student @ UTokyo
Advisor: Masato Okada
Jul.-Sep. 2018 Summer Internship @ PFN
Mar. 2017 MSc. (Science) @ UTokyo
Mar. 2015 B.S. @ Keio Univ.
Interests
Generative Models, Neural Networks, Computational Neuroscience,
Unsupervised Learning
SNS
!: ganow.me / *: ganow / +: @ny_ganow

3. Motivation
ARTICLERESEARCH
Figure 3 | Monte Carlo tree search in AlphaGo. a, Each simulation
traverses the tree by selecting the edge with maximum action value Q,
plus a bonus u(P) that depends on a stored prior probability P for that
is evaluated
a rollout to
Selectiona b cExpansion Evaluation
p
p
Q + u(P)
Q + u(P)Q + u(P)
Q + u(P)
P P
P P
r
P
max
max
P
[Silver+2016]
Mammal
Primate
Human Monkey
Rodent

4. Motivation
Mammal
Primate
Human Monkey
Rodent
ARTICLECH
Monte Carlo tree search in AlphaGo. a, Each simulation
he tree by selecting the edge with maximum action value Q,
is evaluated in two ways: using the value network vθ
a rollout to the end of the game with the fast rollout
Selection b c dExpansion Evaluation Backup
p
p
Q + u(P)
Q + u(P)Q + u(P)
Q + u(P)
P P
P P
Q QQ
Q
rr r
P
max
max
P
[Silver+2016]
Hierarchical Datasets Hyperbolic Space
[Image: wikipedia.org]
[Nickel & Kiela, 2017]

5. Motivation
Mammal
Primate
Human Monkey
Rodent
ARTICLECH
Monte Carlo tree search in AlphaGo. a, Each simulation
he tree by selecting the edge with maximum action value Q,
is evaluated in two ways: using the value network vθ
a rollout to the end of the game with the fast rollout
Selection b c dExpansion Evaluation Backup
p
p
Q + u(P)
Q + u(P)Q + u(P)
Q + u(P)
P P
P P
Q QQ
Q
rr r
P
max
max
P
[Silver+2016]
Hierarchical Datasets Hyperbolic Space
Volume increases exponentially
with its radius

6. Motivation
Mammal
Primate
Human Monkey
Rodent
ARTICLECH
Monte Carlo tree search in AlphaGo. a, Each simulation
he tree by selecting the edge with maximum action value Q,
is evaluated in two ways: using the value network vθ
a rollout to the end of the game with the fast rollout
Selection b c dExpansion Evaluation Backup
p
p
Q + u(P)
Q + u(P)Q + u(P)
Q + u(P)
P P
P P
Q QQ
Q
rr r
P
max
max
P
[Silver+2016]
Hierarchical Datasets Hyperbolic Space
[Nickel+2017]

7. Motivation
Mammal
Primate
Human Monkey
Rodent
ARTICLECH
Monte Carlo tree search in AlphaGo. a, Each simulation
he tree by selecting the edge with maximum action value Q,
is evaluated in two ways: using the value network vθ
a rollout to the end of the game with the fast rollout
Selection b c dExpansion Evaluation Backup
p
p
Q + u(P)
Q + u(P)Q + u(P)
Q + u(P)
P P
P P
Q QQ
Q
rr r
P
max
max
P
[Silver+2016]
Hierarchical Datasets Hyperbolic Space
[Nickel+2017]
How can we extend these works to
probabilistic inference?

8. Difficulty: Probabilistic Distribution on Curved Space
…
M
1.
2. 3.
[Image: wikipedia.org]

9. Difficulty: Probabilistic Distribution on Curved Space
…
M
1.
2. 3.
[Image: wikipedia.org]

10. Difficulty: Probabilistic Distribution on Curved Space
…
M
1.
2. 3.
[Image: wikipedia.org]

11. Difficulty: Probabilistic Distribution on Curved Space
…
M
1.
2. 3.
[Image: wikipedia.org]

12. [ja.wikipedia.org]
(e.g. Poincaré disk, Lorentz model, …)
Lorentz Model
ℝ"#$ Lorentzian product
-1 n :
Hyperbolic Geometry

13. Hyperbolic Geometry
(Exponential Map)
(tangent space)
% ∈ '(ℍ* O
(Parallel Transport)
+ ∈ ',ℍ*
% ∈ '(ℍ*

14. Construction of Hyperbolic Wrapped Distribution
ℝ*
( )

15. Hyperbolic Wrapped Distribution(b)
Figure 3: The heatmaps of log-likelihood of the pesudo-
hyperbolic Gaussians with various µ and Σ. We designate
the origin of hyperbolic space by the × mark. See Ap-
pendix B for further details.
Since the metric at the tangent space coincides with the Eu-
clidean metric, we can produce various types of Hyperbolic
distributions by applying our construction strategy to other
distributions defined on Euclidean space, such as Laplace
and Cauchy distribution.
to a
rep
gra
wor
β-V
a sc
In H
is i
cod
µ
As
allo
dien
of t
rep
4.2
We
bili
lum
tual
wor
on
ing
wri
Density:
Projection:
(910 1
(;2 2 ; 9120 +
) 0 2 9 2 92 (
≃ ℝ* 2

16. Numerical Evaluations: VAEs on Synthetic Data
Hyperbolic VAE
Yoshihiro Nagano 1
Shoichiro Yamaguchi 2
Yasuhiro Fujita 2
Masanori Koyama 2
Abstract
rbolic space is a geometry that is known to
ell-suited for representation learning of data
an underlying hierarchical structure. In this
r, we present a novel hyperbolic distribution
d pseudo-hyperbolic Gaussian, a Gaussian-
distribution on hyperbolic space whose den-
can be evaluated analytically and differen-
d with respect to the parameters. Our dis-
ion enables the gradient-based learning of
robabilistic models on hyperbolic space that
d never have been considered before. Also,
an sample from this hyperbolic probability
bution without resorting to auxiliary means
ejection sampling. As applications of our
bution, we develop a hyperbolic-analog of
tional autoencoder and a method of prob-
tic word embedding on hyperbolic space.
emonstrate the efficacy of our distribution
rious datasets including MNIST, Atari 2600
kout, and WordNet.
duction
hyperbolic geometry is drawing attention as a
geometry to assist deep networks in capturing
tal structural properties of data such as a hi-
Hyperbolic attention network (G¨ulc¸ehre et al.,
proved the generalization performance of neural
on various tasks including machine translation
ng the hyperbolic geometry on several parts of
(a) A tree representation of the
training dataset
(b) Normal VAE (β = 1.0) (c) Hyperbolic VAE
Figure 1: The visual results of Hyperbolic VAE applied to
an artificial dataset generated by applying random pertur-
bations to a binary tree. The visualization is being done
on the Poincar´e ball. The red points are the embeddings
of the original tree, and the blue points are the embeddings
of noisy observations generated from the tree. The pink
× represents the origin of the hyperbolic space. The VAE
was trained without the prior knowledge of the tree struc-
ture. Please see 6.1 for experimental details
determines the properties of the dataset that can be learned
from the embedding. For the dataset with a hierarchical
stribution on Hyperbolic Space for
sed Learning
2
Yasuhiro Fujita 2
Masanori Koyama 2
(a) A tree representation of the
training dataset
(b) Normal VAE (β = 1.0) (c) Hyperbolic VAE
Figure 1: The visual results of Hyperbolic VAE applied to
(

17. Numerical Evaluations: VAEs on Breakout
Atari 2600 Breakout-v4
DQN [Mnih+ 2015]
VAE
(≒
)
Vanilla
Vanilla, |v|2 = 200
VanillaHyperbolic

18. Numerical Evaluations: Word Embeddings
WordNet Nouns word embedding
Euclid [Vilnis & McCallum 2015]

19. Conclusion
projection-based
hyperbolic wrapped distribution
VAE MNIST, Atari 2600
Breakout, WordNet
*: pfnet-research/hyperbolic_wrapped_distribution
+

20. Acknowledgements
Masaki
Watanabe
Tomohiro Hayase Kenta Oono
Takeru Miyato Sosuke Kobayashi
PFN2018