Download to read offline
![Explanation of Degeneracy
Consider a variable x between 0 and 1
with expected value 0.3.
An exponential random model for it is given by:
P(x) = exp( ax + b )
P(x)
We get
Mode[x] = 0
!!
0
Jérôme Kunegis
0
0.3
Generating Networks with Arbitrary Properties
1
x
11](https://image.slidesharecdn.com/presentation-131219045225-phpapp01/85/Generating-Networks-with-Arbitrary-Properties-11-320.jpg)
![Idea
Require not that E[x] = c, but that x follow a normal distribution
P(x)
0
0
0.3
1
x
P(G) = Pnorm (x1, x2, …; μ1, μ2, …, σ1, σ2, …)
Jérôme Kunegis
Generating Networks with Arbitrary Properties
12](https://image.slidesharecdn.com/presentation-131219045225-phpapp01/85/Generating-Networks-with-Arbitrary-Properties-12-320.jpg)
Uploaded byJérôme KUNEGIS
Generating Networks with Arbitrary Properties
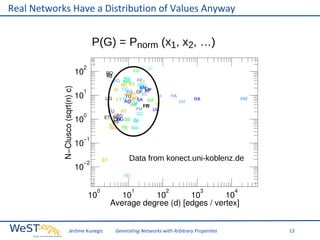
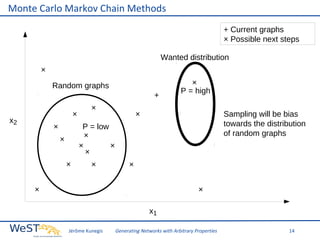
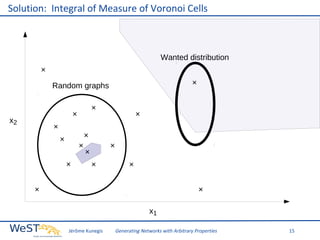
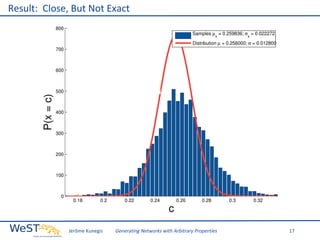
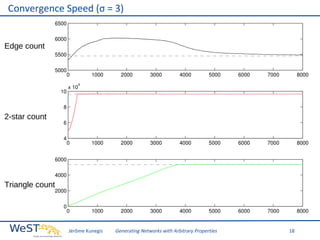
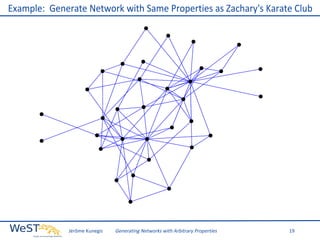
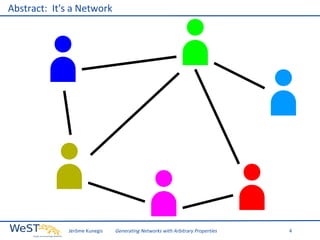
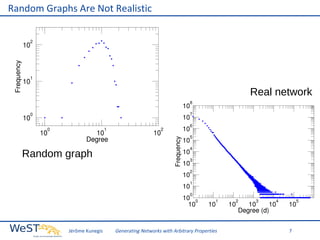
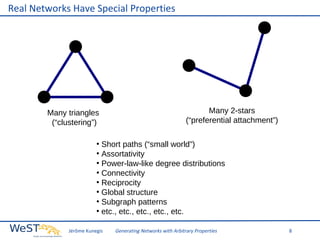
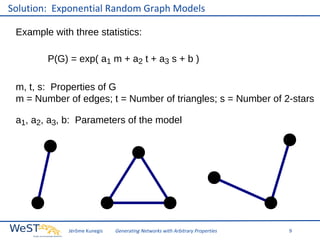
This document discusses generating networks with arbitrary properties. It begins by explaining the limitations of random graphs in capturing properties of real-world networks. Exponential random graph models are then introduced as a way to generate graphs with specific properties, but these models often produce degenerate graphs. The document proposes using a normal distribution over graph properties rather than just expected values. It describes using Monte Carlo Markov chain methods and integrating over Voronoi cells to sample graphs from this distribution. Finally, it shows an example of generating a network with the same properties as the real-world Karate Club network.
More Related Content
Similar to Generating Networks with Arbitrary Properties
![Introduction to bayesian_networks[1]](https://cdn.slidesharecdn.com/ss_thumbnails/introductiontobayesiannetworks1-150525024327-lva1-app6891-thumbnail.jpg?width=640&height=640&fit=bounds)
Generating Networks with Arbitrary Properties
- 1. Generating networks with arbitraryproperties
- 2. Social Interaction “You’re myfriend” Jérôme Kunegis Generating Networks with Arbitrary Properties 2
- 3. Many Social Interactions ” yfriend m You’re “ Jérôme Kunegis ’re m y frie nd” ” nd rie y friend” “You y ’re my frie nd ” f my ’re ou “Y “You’re m ’re ou “Y m d” n ie fr “Yo u y friend m “You’re Generating Networks with Arbitrary Properties ” 3
- 4. Abstract: It's aNetwork Jérôme Kunegis Generating Networks with Arbitrary Properties 4
- 5. Problem: Generate RealisticGraphs Why generate graphs? To visualize an existing network: generate a smaller graph with same properties as a large real (note: sampling a subset will skew the properties) ● For testing algorithms: Generate a larger network then those currently known ● Jérôme Kunegis Generating Networks with Arbitrary Properties 5
- 6. Basic Idea forGenerating Networks: Random Graphs Each edge has probability p of existing Paul Erdős Jérôme Kunegis Generating Networks with Arbitrary Properties 6
- 7. Random Graphs AreNot Realistic Real network Random graph Jérôme Kunegis Generating Networks with Arbitrary Properties 7
- 8. Real Networks HaveSpecial Properties Many triangles (“clustering”) Many 2-stars (“preferential attachment”) Short paths (“small world”) ● Assortativity ● Power-law-like degree distributions ● Connectivity ● Reciprocity ● Global structure ● Subgraph patterns ● etc., etc., etc., etc., etc. ● Jérôme Kunegis Generating Networks with Arbitrary Properties 8
- 9. Solution: Exponential RandomGraph Models Example with three statistics: P(G) = exp( a1 m + a2 t + a3 s + b ) m, t, s: Properties of G m = Number of edges; t = Number of triangles; s = Number of 2-stars a1, a2, a3, b: Parameters of the model Jérôme Kunegis Generating Networks with Arbitrary Properties 9
- 10. Problems of ExponentialRandom Graph Models P(G) = exp( a1 x1 + a2 x2 + … + ak xk + b ) Many exponential random graph models are degenerate: They contain mostly almost-empty or almost-full graphs But on average, they produce the correct statistics! Jérôme Kunegis Generating Networks with Arbitrary Properties 10
- 11. Explanation of Degeneracy Considera variable x between 0 and 1 with expected value 0.3. An exponential random model for it is given by: P(x) = exp( ax + b ) P(x) We get Mode[x] = 0 !! 0 Jérôme Kunegis 0 0.3 Generating Networks with Arbitrary Properties 1 x 11
- 12. Idea Require not thatE[x] = c, but that x follow a normal distribution P(x) 0 0 0.3 1 x P(G) = Pnorm (x1, x2, …; μ1, μ2, …, σ1, σ2, …) Jérôme Kunegis Generating Networks with Arbitrary Properties 12
- 13. Real Networks Havea Distribution of Values Anyway P(G) = Pnorm (x1, x2, …) Data from konect.uni-koblenz.de Jérôme Kunegis Generating Networks with Arbitrary Properties 13
- 14. Monte Carlo MarkovChain Methods + Current graphs × Possible next steps Wanted distribution × Random graphs + × x2 × × × P = high × Sampling will be bias towards the distribution of random graphs P = low × × × × × × × × × × x1 Jérôme Kunegis Generating Networks with Arbitrary Properties 14
- 15. Solution: Integral ofMeasure of Voronoi Cells Wanted distribution × × Random graphs × × x2 × × × × × × × × × × × × x1 Jérôme Kunegis Generating Networks with Arbitrary Properties 15
- 16. How To ComputeThe Integral over Voronoi Cells Answer: We don't have to. Sampling strategy: Sample point in statistic-space according to our wanted distribution ● Find nearest possible network (i.e., nearest “×”) ● Claim: This distribution at each step is similar to the underlying measure, giving an unbiased sampling. Jérôme Kunegis Generating Networks with Arbitrary Properties 16
- 17. Result: Close, ButNot Exact Jérôme Kunegis Generating Networks with Arbitrary Properties 17
- 18. Convergence Speed (σ= 3) Edge count 2-star count Triangle count Jérôme Kunegis Generating Networks with Arbitrary Properties 18
- 19. Example: Generate Networkwith Same Properties as Zachary's Karate Club Jérôme Kunegis Generating Networks with Arbitrary Properties 19