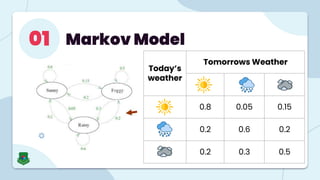
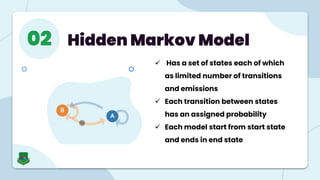
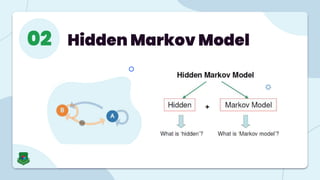
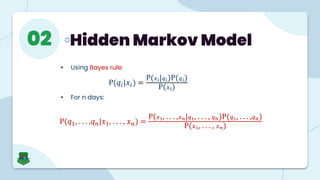
The document provides an overview of Markov Models and Hidden Markov Models (HMMs), detailing their definitions, applications, and problems associated with them. Markov Models are stochastic processes where future states depend only on the current state, while HMMs involve hidden states and observable symbols, with specific algorithms like Baum-Welch and Viterbi used for evaluation, decoding, and learning. Applications of HMMs span various fields, including speech recognition, financial modeling, and time series analysis.

1. 01
Markov Model
HIDDEN MARKOV MODEL
02
HMMs
03
Applications
04
Problems of
HMMs

2. Markov Model
01
 What is Markov Model?
 Example of Markov
Model

3. Markov Model
01
• Stochastic Method
• Randomly Changing Systems
• Next State Is Only Dependent On
The Current State

4. Markov Models
01
• Assume there are three types of weather:
• Weather prediction is about the what would
be the weather tomorrow:
• Based on the observations on the past
• Weather at day n is
• 𝑞𝑛 depends on the weather of the past days
(𝑞𝑛−1, 𝑞𝑛−2,….)
 Sunny
 Rainy
 Foggy

5. Markov Model
01
• We want to find that:
P (𝑞𝑛|𝑞𝑛−1, 𝑞𝑛−2, …. , 𝑞1)
Means given the past weathers what is the
probability of any possible weather of today.

6. Markov Model
01
Today’s
weather
Tomorrows Weather
0.8 0.05 0.15
0.2 0.6 0.2
0.2 0.3 0.5

7. Examples:
• If the weather yesterday was rainy and today is foggy, what is the
probability that tomorrow it will be sunny?
P (𝑞3 = | 𝑞2 = , 𝑞1 = )= P (𝑞3 = | 𝑞2 = )
= 0.2
Markov assumption
Markov Model
01

8. Hidden Markov Model
02
 History
 What is HMMs?
 Variants of HMMs
 Example of HMMs

9. Hidden Markov Model
02
• Introduced in the 1960s
• Baum and Petrie

10. Hidden Markov Model
02
 Has a set of states each of which
as limited number of transitions
and emissions
 Each transition between states
has an assigned probability
 Each model start from start state
and ends in end state

11. Hidden Markov Model
02

12. Variants of HMMs
02
 profile-HMMs
 pair-HMMs
 context-sensitive HMMs

13. Hidden Markov Model
02
• Suppose that you are locked in a room for several days,
• You try to predict the weather outside
• The only piece of evidence you have is whether the
person who comes into the room bringing your daily
meal is carrying an umbrella or not.

14. Hidden Markov Model
02
• Assume probabilities as seen in the table:
Weather Probability of Umbrella
Sunny 0.1
Rainy 0.8
Foggy 0.3
Probability P(𝑥𝑖|𝑞𝑖) of carrying an umbrella (𝑥𝑖 = true) based on the
weather 𝑞𝑖 on some day i

15. Hidden Markov Model
02
• Finding the probability of a certain weather
𝑞𝑛 ∈ { sunny, rainy, foggy }
• Is based on the observations 𝒙𝒊:

16. Hidden Markov Model
02
• Using Bayes rule:
P(𝑞𝑖|𝑥𝑖) =
P(𝑥𝑖|𝑞𝑖)P(𝑞𝑖)
P(𝑥𝑖)
• For n days:
P(𝑞1, . . . ,𝑞𝑛|𝑥1, . . . , 𝑥𝑛) =
P(𝑥1, . . . ,𝑥𝑛|𝑞1, . . . , 𝑞𝑛)P(𝑞1, . . . ,𝑞𝑛)
P(𝑥1, . . . , 𝑥𝑛)

17. Hidden Markov Model
02
- Examples:
• Suppose the day you were locked in it was sunny. The
next day, the caretaker carried an umbrella into the
room.
• You would like to know, what the weather was like on this
second day.

18. Hidden Markov Model
02
An HMM is characterized by:
• N, the number if hidden states
• M, the number of distinct observation symbols per state
• {𝑎𝑖𝑗}, the state transition probability distribution
• {𝑏𝑗𝑘}, the observation symbol probability distribution
• {π𝑖 = P(𝑤(1) = 𝑤𝑖)}, the initial state distribution
• Θ = ({𝑎𝑖𝑗}, {𝑏𝑗𝑘}, {π𝑖}), the complete parameter set of the
model.

19. Problems of HMMs
i Evaluating Problem
Problem
s
ii Decoding Problem
iii Leaning Problem
03

20. Problems
03
• Evaluation problem: Given the model, compute the probability that a
particular output sequence was produced by that model (solved by the
forward algorithm).
• Decoding problem: Given the model, find the most likely sequence of
hidden states which could have generated a given output sequence
(solved by the Viterbi algorithm),
• Learning problem: Given a set of output sequences, find the most likely
set of state transition and output probabilities (solved by the Baum-
Welch algorithm.)

21. Evolution Problem
03
Given model λ = (A, B, π),
what is the probability of occurrence of a particular observation sequence
O ={O1, O2,... Or}. i.e determine the likelihood P(O/λ)
Our goal is to compute the like likelihood of on observation sequence
O = O1, O2, O3.... Given a particular HMM model λ = A, B, π.

22. Decoding Problem
03
 Decoding problem of Hidden Markov Model, One of the three
fundamental problems to be solved under HMM is Decoding problem,
Decoding problem is the way to figure out the best hidden state
sequence using HMM
 Given an HMM λ = (A, B, π) and an observation sequence O = o1, o2, …,
oT, how do we choose the corresponding optimal hidden state
sequence (most likely sequence) Q = q1, q2, …, qT that can best explain
the observations.

23. Decoding Problem
03
Goal: Find single best state sequence.
q* = argmaxq P(q | O, λ) = arg maxq P(q, O | λ)
Define
i.e. the best score (highest probability) along a single path, at
time t, which accounts for the first t observations and ends in
state Si.

24. Learning Problem
03
Given a sequence of observation O = o1, o2, …, oT, estimate the transition and emission
probabilities that are most likely to give O. that is, using the observation sequence and
HMM general structure, determine the HMM model λ = (A, B, π) that best fit training
data.
Question answered by Learning problem:
Given a model structure and a set of sequences, find the model that best fits the data.
Baum-Welch Algorithm: The Baum-Welch algorithm is a specific form of the EM
algorithm tailored for HMMs. It is used for unsupervised learning, where you have
access to a sequence of observations but not to the corresponding hidden states. It
iteratively refines the model's parameters (A, B, and π) until convergence.

25. Learning Problem
03

26. Learning Problem
03
Baum-Welch Algorithm
Time complexity: O(N2 T) · (# iterations)
Guaranteed to increase likelihood P(O | λ) via EM
but not guaranteed to find globally optimal λ *
Practical Issues
• Use multiple training sequences (sum over them)
• Apply smoothing to avoid zero counts and improve generalization (add
pseudocounts)

27. Applications
04
 Computational finance
 speed analysis
 Speech recognition
 Speech synthesis
 Part-of-speech tagging
 Document separation in
scanning solutions
 Machine translation
 Handwriting recognition
 Time series analysis
 Activity recognition
 Sequence classification
 Transportation forecasting

28. References
● https://www.cs.hmc.edu/~yjw/teaching/cs158/lectures/17_19_HMMs.pdf
● https://www.exploredatabase.com/2020/04/decoding-problem-of-hidden-markov-
model.html
● https://www.javatpoint.com/hidden-markov-model-in-machine-learning
● https://youtu.be/KcXOT-PJy1U?si=5EYnzh-WBfUMftC2
● https://youtu.be/F5Wrn_UX4L8?si=OCw-K5NIDELyAW0z
● https://youtu.be/Io_VNym0vkI?si=D-II7GsLRb7RUaEo
● https://www.slideshare.net/shivangisaxena566/hidden-markov-model-ppt
● https://www.javatpoint.com/hidden-markov-model-in-machine-learning

29. Any Questions?

30. Thank You!