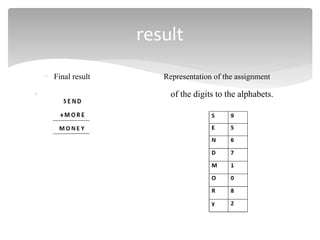
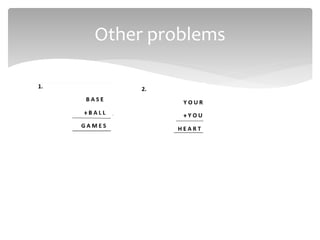
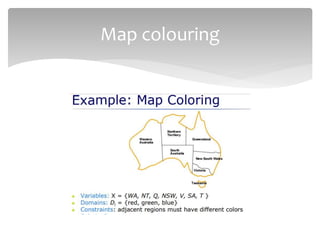
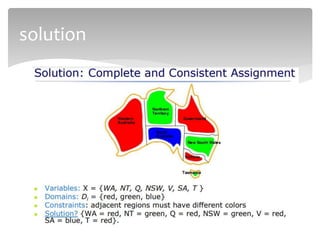
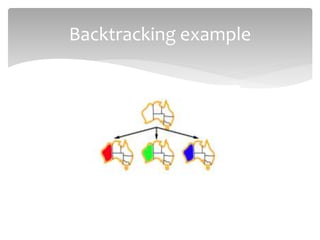
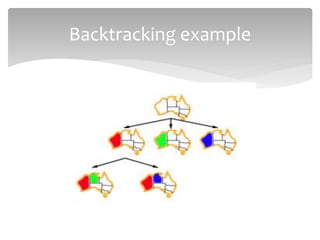
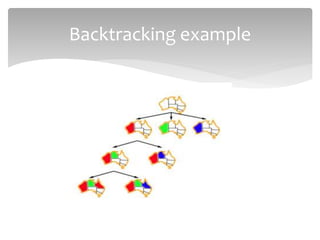
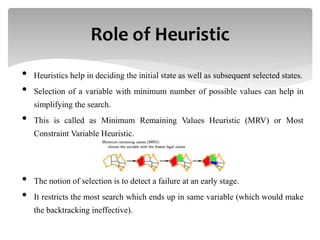
This document discusses constraint satisfaction problems (CSPs). It defines CSPs as problems with variables that must satisfy constraints. CSPs can represent many real-world problems and are solved through constraint satisfaction methods. The document outlines CSP components like variables, domains, and constraints. It also describes representing problems as CSPs, solving CSPs through backtracking search, and the role of heuristics like minimum remaining values in improving the search process.

1. Constraint satisfaction
problems (CSP)
T.ARCHANA
ASSISTANT PROFESSOR
COMPUTER SCIENCE AND ENGINEERING
DEPARTMENT
SRM INSTITUTE OF SCIENCE AND TECHNOLOGY
RAMAPURAM, CHENNAI

2. Introduction to CSP
What is a constraint
Crypto Arithmetic puzzles
Constraint Domain
CSP as a search problem
Backtracking search for CSP
Role of Heuristics
AGENDA

3. • Constraint satisfaction problems (CSPs) are mathematical questions
defined as a set of objects whose state must satisfy a number of constraints
or limitations.
• CSPs represent the entities in a problem as a homogeneous collection of
finite constraints over variables, which is solved by constraint satisfaction
methods.
• It is a search procedure that operates in a space of constraints.
• Any problem in the world can mathematically be represented as CSP.
• The solution is typically a state that can satisfy all the constraints.
INTRODUCTION TO CSP

4. • A constraint satisfaction problem (CSP) consists of
– a set of variables,
– a domain for each variable, and
– a set of constraints.
• The aim is to choose a value for each variable so that the resulting possible
world satisfies the constraints; we want a model of the constraints.
csp

5. • It is mathematical/logical relationship among the attributes of one or more
objects.
• It is important to know the type of constraint.
– Unary Constraint - single variable.
– Binary Constraint - two variable.
– Higher order Constraint - 3 or more variables.
• Constraints can restrict the values of variables.
CONSTRAINT

6. • Assignment problems
– e.g., who teaches what class
• Timetabling problems
– e.g., which class is offered when and where?
• Transportation scheduling
• Factory scheduling
Real-World CSP’s

7.  Constraints:
 1. Variables: can take values from 0-9
 2. No two variables should take same value
 3. The values should be selected such a way that it should comply
with arithmetic properties.

Crypt Arithmetic Puzzles

8. • There should be a unique digit to be replaced with a unique
alphabet.
• The result should satisfy the predefined arithmetic rules, i.e., 2+2
=4, nothing else.
• Digits should be from 0-9 only.
• There should be only one carry forward, while performing the
addition operation on a problem.
• The problem can be solved from both sides, i.e., lefthand side
(L.H.S), or righthand side (R.H.S)
Rules for CSP problem

9.  Given a cryptarithmetic problem,
 i.e., S E N D + M O R E = M O N E Y
 In this example, add both terms S E N D and M O R E to
bring M O N E Y as a result.

problem

10.  Starting from the left hand side (L.H.S) , the terms are S and M.
Assign a digit which could give a satisfactory result.
 Let’s assign S->9 and M->1.
 Hence, we get a satisfactory result by adding up the terms and got an
assignment for O as O->0 as well.
Step 1

11.  Now, move ahead to the next terms E and O to get N as its output.

 Adding E and O, which means 5+0=0, which is not possible
because according to cryptarithmetic constraints, we cannot assign the same
digit to two letters. So, we need to think more and assign some other value.
Step 2

12.  Further, adding the next two terms N and R we get,

 But, we have already assigned E->5. Thus, the above result does not satisfy the values
 because we are getting a different value for E. So, we need to think
more.
 Again, after solving the whole problem, we will get a carryover on this term, so
our answer will be satisfied.
Step 3

13.  Again, on adding the last two terms, i.e., the rightmost
terms D and E, we get Y as its result.

Step 4

14.  Final result Representation of the assignment
 of the digits to the alphabets.
result

15. Other problems

16. • It describes different constrainers, operators, arguments,
variables and their domains.
• It consists of:
1. Legal set of operators
2. Set of variables
3. Set of all types of functions
4. Domain variables
5. Range of variables
constraint domain is five-tuple and represented as
D={var,f,O,dv,rg}
Constraint Domain

17. • A constraint without conjunction is referred as primitive
constraint.
• A conjunction of primitive constraints is called as non-
primitive constraints or generic constraints.
• The constraint problem can be visualized as a constraint
graph.
• nodes represents the groups and the arcs define the
constraint
• One of the prime benefits is the easier representation of
problem in the form of a standard pattern.
Constraint domain

18. • Initial state:
– {} – all variables are unassigned
• Successor function:
– a value is assigned to one of the unassigned variables with no conflict
• Goal test:
– a complete assignment
• Path cost:
– a constant cost for each step
• Solution appears at depth n if there are n variables
CSP as a Search Problem

19. Map colouring

20. • Define the variables to be the regions X = {WA, NT, Q, NSW, V, SA, T}.
• The domain of each variable is the set Di = {red, green, blue}.
• The constraints is C = {SA≠WA, SAW≠NT, SA≠Q, SA≠NSW, SA≠V,
WA≠NT, NT≠Q, Q≠NSW, NSW≠V}.
( SA≠WA is a shortcut for <(SA,WA),SA≠WA>. )
 Constraint graph: The nodes of the graph correspond to variables of
the problem, and a link connects to any two variables that participate in
a constraint.
To formulate a CSP:

21. solution

22. Constraint Graph

23. • Assignment of value to any additional variable within
constraint can generate a legal state (Leads to successor
state in search tree).
• Nodes in a branch backtracks when no options are
available.
• Backtracking allows to go to the previous decision-
making node to eliminate the invalid search space with
respect to constraints.
• Heuristics plays a very important role here.
• If we are in position to determine which variables should
be assigned next, then backtracking can be improved.
Backtracking Search for CSP

24. Algorithm

25. Backtracking example

26. Backtracking example

27. Backtracking example

28. Backtracking example

29. • Heuristics help in deciding the initial state as well as subsequent selected states.
• Selection of a variable with minimum number of possible values can help in
simplifying the search.
• This is called as Minimum Remaining Values Heuristic (MRV) or Most
Constraint Variable Heuristic.
• The notion of selection is to detect a failure at an early stage.
• It restricts the most search which ends up in same variable (which would make
the backtracking ineffective).
Role of Heuristic

30. • MRV cannot have hold on initial selection process.
• Node with maximum constraint is selected over other unassigned
variables - Degree Heuristics.
• By degree heuristics, branching factor cannot be reduced.
• Selection of variables are considered not the values for it.
• So, the order in which the values of particular variable can be
arranged is tackled by least constraining value heuristic.
MRV

31. Thank you