Uploaded byryaekle
579 views

Heizer om10 mod_b

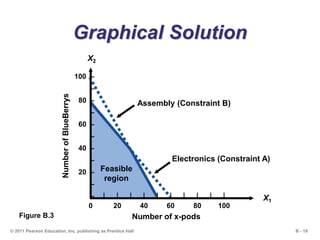
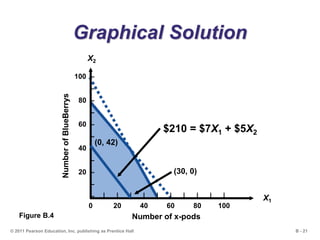
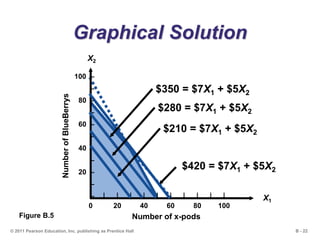
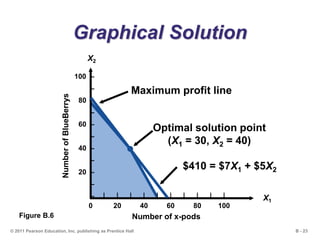
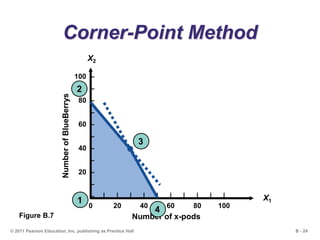
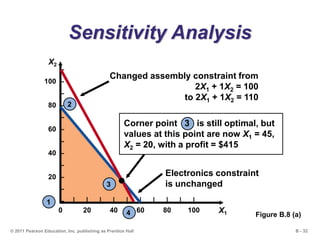
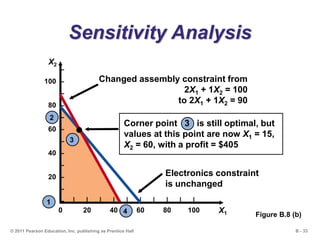
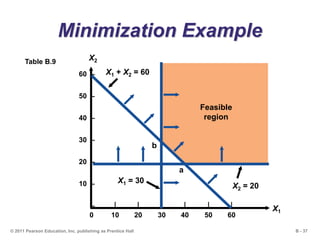
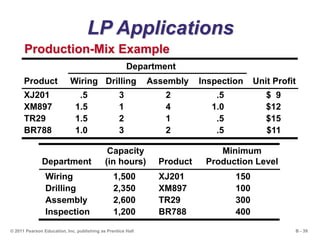
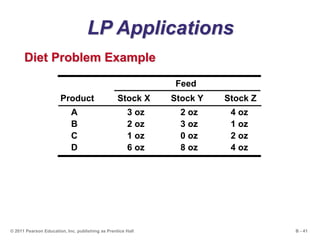
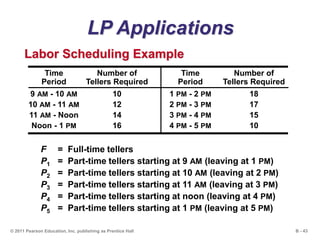
This document outlines the key concepts and steps for solving linear programming problems using graphical and algebraic methods. It begins with an introduction to linear programming and its applications. It then discusses the requirements and formulation of linear programming problems, including defining the objective function and constraints. The document presents examples of solving linear programming graphically using the iso-profit line and corner-point methods. It also covers sensitivity analysis, changes to resources and the objective function, and solving minimization problems. The overall learning objectives are presented to understand how to model, graphically solve, perform sensitivity analysis on, and apply linear programming problems.

Embed presentation

B - 1© 2011 Pearson Education, Inc. publishing as Prentice Hall B Linear Programming PowerPoint presentation to accompany Heizer and Render Operations Management, 10e Principles of Operations Management, 8e PowerPoint slides by Jeff Heyl
B - 2© 2011 Pearson Education, Inc. publishing as Prentice Hall Outline  Why Use Linear Programming?  Requirements of a Linear Programming Problem  Formulating Linear Programming Problems  Shader Electronics Example
B - 3© 2011 Pearson Education, Inc. publishing as Prentice Hall Outline – Continued  Graphical Solution to a Linear Programming Problem  Graphical Representation of Constraints  Iso-Profit Line Solution Method  Corner-Point Solution Method
B - 4© 2011 Pearson Education, Inc. publishing as Prentice Hall Outline – Continued  Sensitivity Analysis  Sensitivity Report  Changes in the Resources of the Right-Hand-Side Values  Changes in the Objective Function Coefficient  Solving Minimization Problems
B - 5© 2011 Pearson Education, Inc. publishing as Prentice Hall Outline – Continued  Linear Programming Applications  Production-Mix Example  Diet Problem Example  Labor Scheduling Example  The Simplex Method of LP
B - 6© 2011 Pearson Education, Inc. publishing as Prentice Hall Learning Objectives When you complete this module you should be able to: 1. Formulate linear programming models, including an objective function and constraints 2. Graphically solve an LP problem with the iso-profit line method 3. Graphically solve an LP problem with the corner-point method
B - 7© 2011 Pearson Education, Inc. publishing as Prentice Hall Learning Objectives When you complete this module you should be able to: 4. Interpret sensitivity analysis and shadow prices 5. Construct and solve a minimization problem 6. Formulate production-mix, diet, and labor scheduling problems
B - 8© 2011 Pearson Education, Inc. publishing as Prentice Hall Why Use Linear Programming?  A mathematical technique to help plan and make decisions relative to the trade-offs necessary to allocate resources  Will find the minimum or maximum value of the objective  Guarantees the optimal solution to the model formulated
B - 9© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications 1. Scheduling school buses to minimize total distance traveled 2. Allocating police patrol units to high crime areas in order to minimize response time to 911 calls 3. Scheduling tellers at banks so that needs are met during each hour of the day while minimizing the total cost of labor
B - 10© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications 4. Selecting the product mix in a factory to make best use of machine- and labor-hours available while maximizing the firm’s profit 5. Picking blends of raw materials in feed mills to produce finished feed combinations at minimum costs 6. Determining the distribution system that will minimize total shipping cost
B - 11© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications 7. Developing a production schedule that will satisfy future demands for a firm’s product and at the same time minimize total production and inventory costs 8. Allocating space for a tenant mix in a new shopping mall so as to maximize revenues to the leasing company
B - 12© 2011 Pearson Education, Inc. publishing as Prentice Hall Requirements of an LP Problem 1. LP problems seek to maximize or minimize some quantity (usually profit or cost) expressed as an objective function 2. The presence of restrictions, or constraints, limits the degree to which we can pursue our objective
B - 13© 2011 Pearson Education, Inc. publishing as Prentice Hall Requirements of an LP Problem 3. There must be alternative courses of action to choose from 4. The objective and constraints in linear programming problems must be expressed in terms of linear equations or inequalities
B - 14© 2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems The product-mix problem at Shader Electronics  Two products 1. Shader x-pod, a portable music player 2. Shader BlueBerry, an internet- connected color telephone  Determine the mix of products that will produce the maximum profit
B - 15© 2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems x-pods BlueBerrys Available Hours Department (X1) (X2) This Week Hours Required to Produce 1 Unit Electronic 4 3 240 Assembly 2 1 100 Profit per unit $7 $5 Decision Variables: X1 = number of x-pods to be produced X2 = number of BlueBerrys to be produced Table B.1
B - 16© 2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems Objective Function: Maximize Profit = $7X1 + $5X2 There are three types of constraints  Upper limits where the amount used is ≤ the amount of a resource  Lower limits where the amount used is ≥ the amount of the resource  Equalities where the amount used is = the amount of the resource
B - 17© 2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems Second Constraint: 2X1 + 1X2 ≤ 100 (hours of assembly time) Assembly time available Assembly time used is ≤ First Constraint: 4X1 + 3X2 ≤ 240 (hours of electronic time) Electronic time available Electronic time used is ≤
B - 18© 2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution  Can be used when there are two decision variables 1. Plot the constraint equations at their limits by converting each equation to an equality 2. Identify the feasible solution space 3. Create an iso-profit line based on the objective function 4. Move this line outwards until the optimal point is identified
B - 19© 2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Assembly (Constraint B) Electronics (Constraint A) Feasible region Figure B.3
B - 20© 2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Assembly (Constraint B) Electronics (Constraint A) Feasible region Figure B.3 Iso-Profit Line Solution Method Choose a possible value for the objective function $210 = 7X1 + 5X2 Solve for the axis intercepts of the function and plot the line X2 = 42 X1 = 30
B - 21© 2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Figure B.4 (0, 42) (30, 0) $210 = $7X1 + $5X2
B - 22© 2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Figure B.5 $210 = $7X1 + $5X2 $420 = $7X1 + $5X2 $350 = $7X1 + $5X2 $280 = $7X1 + $5X2
B - 23© 2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Figure B.6 $410 = $7X1 + $5X2 Maximum profit line Optimal solution point (X1 = 30, X2 = 40)
B - 24© 2011 Pearson Education, Inc. publishing as Prentice Hall 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Corner-Point Method Figure B.7 1 2 3 4
B - 25© 2011 Pearson Education, Inc. publishing as Prentice Hall Corner-Point Method  The optimal value will always be at a corner point  Find the objective function value at each corner point and choose the one with the highest profit Point 1 : (X1 = 0, X2 = 0) Profit $7(0) + $5(0) = $0 Point 2 : (X1 = 0, X2 = 80) Profit $7(0) + $5(80) = $400 Point 4 : (X1 = 50, X2 = 0) Profit $7(50) + $5(0) = $350
B - 26© 2011 Pearson Education, Inc. publishing as Prentice Hall Corner-Point Method  The optimal value will always be at a corner point  Find the objective function value at each corner point and choose the one with the highest profit Point 1 : (X1 = 0, X2 = 0) Profit $7(0) + $5(0) = $0 Point 2 : (X1 = 0, X2 = 80) Profit $7(0) + $5(80) = $400 Point 4 : (X1 = 50, X2 = 0) Profit $7(50) + $5(0) = $350 Solve for the intersection of two constraints 2X1 + 1X2 ≤ 100 (assembly time) 4X1 + 3X2 ≤ 240 (electronics time) 4X1 + 3X2 = 240 - 4X1 - 2X2 = -200 + 1X2 = 40 4X1 + 3(40) = 240 4X1 + 120 = 240 X1 = 30
B - 27© 2011 Pearson Education, Inc. publishing as Prentice Hall Corner-Point Method  The optimal value will always be at a corner point  Find the objective function value at each corner point and choose the one with the highest profit Point 1 : (X1 = 0, X2 = 0) Profit $7(0) + $5(0) = $0 Point 2 : (X1 = 0, X2 = 80) Profit $7(0) + $5(80) = $400 Point 4 : (X1 = 50, X2 = 0) Profit $7(50) + $5(0) = $350 Point 3 : (X1 = 30, X2 = 40) Profit $7(30) + $5(40) = $410
B - 28© 2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Analysis  How sensitive the results are to parameter changes  Change in the value of coefficients  Change in a right-hand-side value of a constraint  Trial-and-error approach  Analytic postoptimality method
B - 29© 2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Report Program B.1
B - 30© 2011 Pearson Education, Inc. publishing as Prentice Hall Changes in Resources  The right-hand-side values of constraint equations may change as resource availability changes  The shadow price of a constraint is the change in the value of the objective function resulting from a one-unit change in the right-hand- side value of the constraint
B - 31© 2011 Pearson Education, Inc. publishing as Prentice Hall Changes in Resources  Shadow prices are often explained as answering the question “How much would you pay for one additional unit of a resource?”  Shadow prices are only valid over a particular range of changes in right- hand-side values  Sensitivity reports provide the upper and lower limits of this range
B - 32© 2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Analysis – 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 X1 X2 Figure B.8 (a) Changed assembly constraint from 2X1 + 1X2 = 100 to 2X1 + 1X2 = 110 Electronics constraint is unchanged Corner point 3 is still optimal, but values at this point are now X1 = 45, X2 = 20, with a profit = $415 1 2 3 4
B - 33© 2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Analysis – 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 X1 X2 Figure B.8 (b) Changed assembly constraint from 2X1 + 1X2 = 100 to 2X1 + 1X2 = 90 Electronics constraint is unchanged Corner point 3 is still optimal, but values at this point are now X1 = 15, X2 = 60, with a profit = $405 1 2 3 4
B - 34© 2011 Pearson Education, Inc. publishing as Prentice Hall Changes in the Objective Function  A change in the coefficients in the objective function may cause a different corner point to become the optimal solution  The sensitivity report shows how much objective function coefficients may change without changing the optimal solution point
B - 35© 2011 Pearson Education, Inc. publishing as Prentice Hall Solving Minimization Problems  Formulated and solved in much the same way as maximization problems  In the graphical approach an iso- cost line is used  The objective is to move the iso- cost line inwards until it reaches the lowest cost corner point
B - 36© 2011 Pearson Education, Inc. publishing as Prentice Hall Minimization Example X1 = number of tons of black-and-white picture chemical produced X2 = number of tons of color picture chemical produced Minimize total cost = 2,500X1 + 3,000X2 Subject to: X1 ≥ 30 tons of black-and-white chemical X2 ≥ 20 tons of color chemical X1 + X2 ≥ 60 tons total X1, X2 ≥ $0 nonnegativity requirements
B - 37© 2011 Pearson Education, Inc. publishing as Prentice Hall Minimization Example Table B.9 60 – 50 – 40 – 30 – 20 – 10 – –| | | | | | | 0 10 20 30 40 50 60 X1 X2 Feasible region X1 = 30 X2 = 20 X1 + X2 = 60 b a
B - 38© 2011 Pearson Education, Inc. publishing as Prentice Hall Minimization Example Total cost at a = 2,500X1 + 3,000X2 = 2,500 (40) + 3,000(20) = $160,000 Total cost at b = 2,500X1 + 3,000X2 = 2,500 (30) + 3,000(30) = $165,000 Lowest total cost is at point a
B - 39© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications Production-Mix Example Department Product Wiring Drilling Assembly Inspection Unit Profit XJ201 .5 3 2 .5 $ 9 XM897 1.5 1 4 1.0 $12 TR29 1.5 2 1 .5 $15 BR788 1.0 3 2 .5 $11 Capacity Minimum Department (in hours) Product Production Level Wiring 1,500 XJ201 150 Drilling 2,350 XM897 100 Assembly 2,600 TR29 300 Inspection 1,200 BR788 400
B - 40© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications X1 = number of units of XJ201 produced X2 = number of units of XM897 produced X3 = number of units of TR29 produced X4 = number of units of BR788 produced Maximize profit = 9X1 + 12X2 + 15X3 + 11X4 subject to .5X1 + 1.5X2 + 1.5X3 + 1X4 ≤ 1,500 hours of wiring 3X1 + 1X2 + 2X3 + 3X4 ≤ 2,350 hours of drilling 2X1 + 4X2 + 1X3 + 2X4 ≤ 2,600 hours of assembly .5X1 + 1X2 + .5X3 + .5X4 ≤ 1,200 hours of inspection X1 ≥ 150 units of XJ201 X2 ≥ 100 units of XM897 X3 ≥ 300 units of TR29 X4 ≥ 400 units of BR788
B - 41© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications Diet Problem Example A 3 oz 2 oz 4 oz B 2 oz 3 oz 1 oz C 1 oz 0 oz 2 oz D 6 oz 8 oz 4 oz Feed Product Stock X Stock Y Stock Z
B - 42© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications X1 = number of pounds of stock X purchased per cow each month X2 = number of pounds of stock Y purchased per cow each month X3 = number of pounds of stock Z purchased per cow each month Minimize cost = .02X1 + .04X2 + .025X3 Ingredient A requirement: 3X1 + 2X2 + 4X3 ≥ 64 Ingredient B requirement: 2X1 + 3X2 + 1X3 ≥ 80 Ingredient C requirement: 1X1 + 0X2 + 2X3 ≥ 16 Ingredient D requirement: 6X1 + 8X2 + 4X3 ≥ 128 Stock Z limitation: X3 ≤ 80 X1, X2, X3 ≥ 0 Cheapest solution is to purchase 40 pounds of grain X at a cost of $0.80 per cow
B - 43© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications Labor Scheduling Example F = Full-time tellers P1 = Part-time tellers starting at 9 AM (leaving at 1 PM) P2 = Part-time tellers starting at 10 AM (leaving at 2 PM) P3 = Part-time tellers starting at 11 AM (leaving at 3 PM) P4 = Part-time tellers starting at noon (leaving at 4 PM) P5 = Part-time tellers starting at 1 PM (leaving at 5 PM) Time Number of Time Number of Period Tellers Required Period Tellers Required 9 AM - 10 AM 10 1 PM - 2 PM 18 10 AM - 11 AM 12 2 PM - 3 PM 17 11 AM - Noon 14 3 PM - 4 PM 15 Noon - 1 PM 16 4 PM - 5 PM 10
B - 44© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications = $75F + $24(P1 + P2 + P3 + P4 + P5) Minimize total daily manpower cost F + P1 ≥ 10 (9 AM - 10 AM needs) F + P1 + P2 ≥ 12 (10 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 ≥ 14 (11 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 + P4 ≥ 16 (noon - 1 PM needs) F + P2 + P3 + P4 + P5 ≥ 18 (1 PM - 2 PM needs) F + P3 + P4 + P5 ≥ 17 (2 PM - 3 PM needs) F + P4 + P5 ≥ 15 (3 PM - 7 PM needs) F + P5 ≥ 10 (4 PM - 5 PM needs) F ≤ 12 4(P1 + P2 + P3 + P4 + P5) ≤ .50(10 + 12 + 14 + 16 + 18 + 17 + 15 + 10)
B - 45© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications = $75F + $24(P1 + P2 + P3 + P4 + P5) Minimize total daily manpower cost F + P1 ≥ 10 (9 AM - 10 AM needs) F + P1 + P2 ≥ 12 (10 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 ≥ 14 (11 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 + P4 ≥ 16 (noon - 1 PM needs) F + P2 + P3 + P4 + P5 ≥ 18 (1 PM - 2 PM needs) F + P3 + P4 + P5 ≥ 17 (2 PM - 3 PM needs) F + P4 + P5 ≥ 15 (3 PM - 7 PM needs) F + P5 ≥ 10 (4 PM - 5 PM needs) F ≤ 12 4(P1 + P2 + P3 + P4 + P5) ≤ .50(112) F, P1, P2, P3, P4, P5 ≥ 0
B - 46© 2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications There are two alternate optimal solutions to this problem but both will cost $1,086 per day F = 10 F = 10 P1 = 0 P1 = 6 P2 = 7 P2 = 1 P3 = 2 P3 = 2 P4 = 2 P4 = 2 P5 = 3 P5 = 3 First Second Solution Solution
B - 47© 2011 Pearson Education, Inc. publishing as Prentice Hall The Simplex Method  Real world problems are too complex to be solved using the graphical method  The simplex method is an algorithm for solving more complex problems  Developed by George Dantzig in the late 1940s  Most computer-based LP packages use the simplex method
B - 48© 2011 Pearson Education, Inc. publishing as Prentice Hall All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printed in the United States of America.

More Related Content

PPT
Taylor introms10 ppt_02
byQA Cmu
 
PDF
Heizer om10 ch01
byryaekle
 
PDF
Heizer om10 ch12
byryaekle
 
PPT
Rsh qam11 ch07 ge
byFiras Husseini
 
PDF
Heizer om10 ch10
byryaekle
 
PDF
Heizer om10 ch13
byryaekle
 
PPT
360_ch04
byryaekle
 
PDF
Heizer om10 mod_e
byryaekle
 
Taylor introms10 ppt_02
byQA Cmu
 
Heizer om10 ch01
byryaekle
 
Heizer om10 ch12
byryaekle
 
Rsh qam11 ch07 ge
byFiras Husseini
 
Heizer om10 ch10
byryaekle
 
Heizer om10 ch13
byryaekle
 
360_ch04
byryaekle
 
Heizer om10 mod_e
byryaekle
 

Viewers also liked

PDF
Heizer om10 mod_a
byryaekle
 
PDF
Heizer om10 ch17
byryaekle
 
PDF
Heizer om10 ch05
byryaekle
 
PDF
Heizer om10 mod_f
byryaekle
 
PDF
Heizer om10 ch14
byryaekle
 
PPT
360_ch02
byryaekle
 
PDF
Heizer om10 ch15
byryaekle
 
PPT
Heizer om10 ch14
byremilaw
 
PPT
360_ch01
byryaekle
 
PPT
360_ch03
byryaekle
 
PDF
Heizer om10 ch02
byRozaimi Mohd Saad
 
PDF
Heizer om10 ch07-process startegy
byRozaimi Mohd Saad
 
PDF
Heizer om10 ch08-location
byRozaimi Mohd Saad
 
PDF
Heizer om10 ch14-mrp
byRozaimi Mohd Saad
 
PDF
Heizer om10 ch17-maintenance and reliability
byRozaimi Mohd Saad
 
PDF
Heizer om10 ch16-jit and lean operations
byRozaimi Mohd Saad
 
PDF
Heizer om10 mod_c
byryaekle
 
PDF
Heizer om10 ch07
byryaekle
 
PDF
Heizer om10 ch04
byRozaimi Mohd Saad
 
PDF
Bad410 business law
byryaekle
 
Heizer om10 mod_a
byryaekle
 
Heizer om10 ch17
byryaekle
 
Heizer om10 ch05
byryaekle
 
Heizer om10 mod_f
byryaekle
 
Heizer om10 ch14
byryaekle
 
360_ch02
byryaekle
 
Heizer om10 ch15
byryaekle
 
Heizer om10 ch14
byremilaw
 
360_ch01
byryaekle
 
360_ch03
byryaekle
 
Heizer om10 ch02
byRozaimi Mohd Saad
 
Heizer om10 ch07-process startegy
byRozaimi Mohd Saad
 
Heizer om10 ch08-location
byRozaimi Mohd Saad
 
Heizer om10 ch14-mrp
byRozaimi Mohd Saad
 
Heizer om10 ch17-maintenance and reliability
byRozaimi Mohd Saad
 
Heizer om10 ch16-jit and lean operations
byRozaimi Mohd Saad
 
Heizer om10 mod_c
byryaekle
 
Heizer om10 ch07
byryaekle
 
Heizer om10 ch04
byRozaimi Mohd Saad
 
Bad410 business law
byryaekle
 

Similar to Heizer om10 mod_b

PPTX
heizer_om12_MB final.pptx Linear Programming
bymohamedzakar1
 
PPT
modB.ppt modA.ppt operation management slide for business
byMHammadMasood
 
PPT
lp.ppt finance,, Rajshahi University -RU
bymahedi11
 
PPTX
linear programing is the model that can be
byBegetaChalkut
 
PPT
LinearProgramming-Graphicalnethod.ppt
byMayurkumarpatil1
 
PPT
Mathematics For Management CHAPTER THREE PART I.PPT
byAYNETUTEREFE1
 
PPTX
lec 9.pptxZXXXXxzZXZxZxZxZXZXZXZxZxZxzxzXZXZX
byYumnaShahzaad
 
PDF
Linear Models for Engineering applications
byKalinduDilanjan
 
PPTX
Linear programming - Model formulation, Graphical Method
byJoseph Konnully
 
PPTX
LINEAR PROGRAMMING
byrashi9
 
PPTX
Linear programming
byCollege of Fisheries, KVAFSU, Mangalore, Karnataka
 
PPT
Heizer mod b
byharsha-JSSGIW
 
PPTX
Linear Programing.pptx
byAdnanHaleem
 
PPT
Heizer mod b
byRizwan Khurram
 
PPTX
Linear Programming
byPulchowk Campus
 
PPTX
Evans_Analytics2e_ppt_13.pptxbbbbbbbbbbb
byVikasRai405977
 
PPTX
LPP.pptx
byRajeevRanjan743854
 
PPT
1 resource optimization 2
byshushay hailu
 
PPTX
Quantitativetechniqueformanagerialdecisionlinearprogramming 090725035417-phpa...
bykongara
 
PPTX
Graphical Method_LPP(QA-Render-052021) (1).pptx
bydhakalgopal
 
heizer_om12_MB final.pptx Linear Programming
bymohamedzakar1
 
modB.ppt modA.ppt operation management slide for business
byMHammadMasood
 
lp.ppt finance,, Rajshahi University -RU
bymahedi11
 
linear programing is the model that can be
byBegetaChalkut
 
LinearProgramming-Graphicalnethod.ppt
byMayurkumarpatil1
 
Mathematics For Management CHAPTER THREE PART I.PPT
byAYNETUTEREFE1
 
lec 9.pptxZXXXXxzZXZxZxZxZXZXZXZxZxZxzxzXZXZX
byYumnaShahzaad
 
Linear Models for Engineering applications
byKalinduDilanjan
 
Linear programming - Model formulation, Graphical Method
byJoseph Konnully
 
LINEAR PROGRAMMING
byrashi9
 
Linear programming
byCollege of Fisheries, KVAFSU, Mangalore, Karnataka
 
Heizer mod b
byharsha-JSSGIW
 
Linear Programing.pptx
byAdnanHaleem
 
Heizer mod b
byRizwan Khurram
 
Linear Programming
byPulchowk Campus
 
Evans_Analytics2e_ppt_13.pptxbbbbbbbbbbb
byVikasRai405977
 
LPP.pptx
byRajeevRanjan743854
 
1 resource optimization 2
byshushay hailu
 
Quantitativetechniqueformanagerialdecisionlinearprogramming 090725035417-phpa...
bykongara
 
Graphical Method_LPP(QA-Render-052021) (1).pptx
bydhakalgopal
 

More from ryaekle

PDF
Heizer om10 ch16
byryaekle
 
PDF
Heizer om10 mod_d
byryaekle
 
PDF
Heizer om10 ch09
byryaekle
 
PDF
Heizer om10 ch11
byryaekle
 
PDF
Heizer om10 ch06
byryaekle
 
PDF
Heizer om10 ch08
byryaekle
 
PPT
p305_pp11
byryaekle
 
PDF
Bad360 operations management online
byryaekle
 
PPT
p305_pp10
byryaekle
 
PPT
p305_pp12
byryaekle
 
DOCX
Human resources assignment
byryaekle
 
PPT
p305_pp08
byryaekle
 
PPT
0132886391 pp09
byryaekle
 
PPT
p305_pp07
byryaekle
 
PPT
p305_pp05
byryaekle
 
PPT
p305_pp06
byryaekle
 
PDF
Meet your professor
byryaekle
 
Heizer om10 ch16
byryaekle
 
Heizer om10 mod_d
byryaekle
 
Heizer om10 ch09
byryaekle
 
Heizer om10 ch11
byryaekle
 
Heizer om10 ch06
byryaekle
 
Heizer om10 ch08
byryaekle
 
p305_pp11
byryaekle
 
Bad360 operations management online
byryaekle
 
p305_pp10
byryaekle
 
p305_pp12
byryaekle
 
Human resources assignment
byryaekle
 
p305_pp08
byryaekle
 
0132886391 pp09
byryaekle
 
p305_pp07
byryaekle
 
p305_pp05
byryaekle
 
p305_pp06
byryaekle
 
Meet your professor
byryaekle
 

Recently uploaded

PDF
DevFest El Jadida 2025 - Product Thinking
byElmehdi AMLOU
 
PDF
Digit Expo 2025 - EICC Edinburgh 27th November
byRay Bugg
 
PPTX
Conversational Agents – Building Intelligent Assistants [Virtual Hands-on Wor...
byUiPathCommunity
 
PDF
API-First Architecture in Financial Systems
bycyy111112
 
PDF
Energy Storage Landscape Clean Energy Ministerial
bySurajitBanerjee38
 
PPTX
Unit-4-ARTIFICIAL NEURAL NETWORKS.pptx ANN ppt Artificial neural network
byssuserd4481a
 
PDF
ElyriaSoftware — Powering the Future with Blockchain Innovation
byElyria Software
 
PDF
December Patch Tuesday
byIvanti
 
PDF
Day 5 - Red Team + Blue Team in the Cloud - 2nd Sight Lab Cloud Security Class
by2nd Sight Lab
 
PDF
The year in review - MarvelClient in 2025
bypanagenda
 
PDF
Making Sense of Raster: From Bit Depth to Better Workflows
bySafe Software
 
PDF
Our Digital Tribe_ Cultivating Connection and Growth in Our Slack Community 🌿...
bysanjeetmishra30
 
DOCX
Introduction to the World of Computers (Hardware & Software)
byALIABBAS ABASOV
 
PPTX
From Backup to Resilience: How MSPs Are Preparing for 2026
byMSP360
 
PPT
software-security-intro in information security.ppt
byismaeelsahib032
 
PDF
Eredità digitale sugli smartphone: cosa resta di noi nei dispositivi mobili
bySpeck&Tech
 
PDF
Session 1 - Solving Semi-Structured Documents with Document Understanding
byDianaGray10
 
PPTX
THIS IS CYBER SECURITY NOTES USED IN CLASS ON VARIOUS TOPICS USED IN CYBERSEC...
byMelissaGblinwon
 
PPTX
Data Privacy and Protection: Safeguarding Information in a Connected World
byYasir Naveed Riaz
 
PPTX
AI in Cybersecurity: Digital Defense by Yasir Naveed Riaz
byYasir Naveed Riaz
 
DevFest El Jadida 2025 - Product Thinking
byElmehdi AMLOU
 
Digit Expo 2025 - EICC Edinburgh 27th November
byRay Bugg
 
Conversational Agents – Building Intelligent Assistants [Virtual Hands-on Wor...
byUiPathCommunity
 
API-First Architecture in Financial Systems
bycyy111112
 
Energy Storage Landscape Clean Energy Ministerial
bySurajitBanerjee38
 
Unit-4-ARTIFICIAL NEURAL NETWORKS.pptx ANN ppt Artificial neural network
byssuserd4481a
 
ElyriaSoftware — Powering the Future with Blockchain Innovation
byElyria Software
 
December Patch Tuesday
byIvanti
 
Day 5 - Red Team + Blue Team in the Cloud - 2nd Sight Lab Cloud Security Class
by2nd Sight Lab
 
The year in review - MarvelClient in 2025
bypanagenda
 
Making Sense of Raster: From Bit Depth to Better Workflows
bySafe Software
 
Our Digital Tribe_ Cultivating Connection and Growth in Our Slack Community 🌿...
bysanjeetmishra30
 
Introduction to the World of Computers (Hardware & Software)
byALIABBAS ABASOV
 
From Backup to Resilience: How MSPs Are Preparing for 2026
byMSP360
 
software-security-intro in information security.ppt
byismaeelsahib032
 
Eredità digitale sugli smartphone: cosa resta di noi nei dispositivi mobili
bySpeck&Tech
 
Session 1 - Solving Semi-Structured Documents with Document Understanding
byDianaGray10
 
THIS IS CYBER SECURITY NOTES USED IN CLASS ON VARIOUS TOPICS USED IN CYBERSEC...
byMelissaGblinwon
 
Data Privacy and Protection: Safeguarding Information in a Connected World
byYasir Naveed Riaz
 
AI in Cybersecurity: Digital Defense by Yasir Naveed Riaz
byYasir Naveed Riaz
 

Heizer om10 mod_b

  • 1.
    B - 1©2011 Pearson Education, Inc. publishing as Prentice Hall B Linear Programming PowerPoint presentation to accompany Heizer and Render Operations Management, 10e Principles of Operations Management, 8e PowerPoint slides by Jeff Heyl
  • 2.
    B - 2©2011 Pearson Education, Inc. publishing as Prentice Hall Outline  Why Use Linear Programming?  Requirements of a Linear Programming Problem  Formulating Linear Programming Problems  Shader Electronics Example
  • 3.
    B - 3©2011 Pearson Education, Inc. publishing as Prentice Hall Outline – Continued  Graphical Solution to a Linear Programming Problem  Graphical Representation of Constraints  Iso-Profit Line Solution Method  Corner-Point Solution Method
  • 4.
    B - 4©2011 Pearson Education, Inc. publishing as Prentice Hall Outline – Continued  Sensitivity Analysis  Sensitivity Report  Changes in the Resources of the Right-Hand-Side Values  Changes in the Objective Function Coefficient  Solving Minimization Problems
  • 5.
    B - 5©2011 Pearson Education, Inc. publishing as Prentice Hall Outline – Continued  Linear Programming Applications  Production-Mix Example  Diet Problem Example  Labor Scheduling Example  The Simplex Method of LP
  • 6.
    B - 6©2011 Pearson Education, Inc. publishing as Prentice Hall Learning Objectives When you complete this module you should be able to: 1. Formulate linear programming models, including an objective function and constraints 2. Graphically solve an LP problem with the iso-profit line method 3. Graphically solve an LP problem with the corner-point method
  • 7.
    B - 7©2011 Pearson Education, Inc. publishing as Prentice Hall Learning Objectives When you complete this module you should be able to: 4. Interpret sensitivity analysis and shadow prices 5. Construct and solve a minimization problem 6. Formulate production-mix, diet, and labor scheduling problems
  • 8.
    B - 8©2011 Pearson Education, Inc. publishing as Prentice Hall Why Use Linear Programming?  A mathematical technique to help plan and make decisions relative to the trade-offs necessary to allocate resources  Will find the minimum or maximum value of the objective  Guarantees the optimal solution to the model formulated
  • 9.
    B - 9©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications 1. Scheduling school buses to minimize total distance traveled 2. Allocating police patrol units to high crime areas in order to minimize response time to 911 calls 3. Scheduling tellers at banks so that needs are met during each hour of the day while minimizing the total cost of labor
  • 10.
    B - 10©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications 4. Selecting the product mix in a factory to make best use of machine- and labor-hours available while maximizing the firm’s profit 5. Picking blends of raw materials in feed mills to produce finished feed combinations at minimum costs 6. Determining the distribution system that will minimize total shipping cost
  • 11.
    B - 11©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications 7. Developing a production schedule that will satisfy future demands for a firm’s product and at the same time minimize total production and inventory costs 8. Allocating space for a tenant mix in a new shopping mall so as to maximize revenues to the leasing company
  • 12.
    B - 12©2011 Pearson Education, Inc. publishing as Prentice Hall Requirements of an LP Problem 1. LP problems seek to maximize or minimize some quantity (usually profit or cost) expressed as an objective function 2. The presence of restrictions, or constraints, limits the degree to which we can pursue our objective
  • 13.
    B - 13©2011 Pearson Education, Inc. publishing as Prentice Hall Requirements of an LP Problem 3. There must be alternative courses of action to choose from 4. The objective and constraints in linear programming problems must be expressed in terms of linear equations or inequalities
  • 14.
    B - 14©2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems The product-mix problem at Shader Electronics  Two products 1. Shader x-pod, a portable music player 2. Shader BlueBerry, an internet- connected color telephone  Determine the mix of products that will produce the maximum profit
  • 15.
    B - 15©2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems x-pods BlueBerrys Available Hours Department (X1) (X2) This Week Hours Required to Produce 1 Unit Electronic 4 3 240 Assembly 2 1 100 Profit per unit $7 $5 Decision Variables: X1 = number of x-pods to be produced X2 = number of BlueBerrys to be produced Table B.1
  • 16.
    B - 16©2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems Objective Function: Maximize Profit = $7X1 + $5X2 There are three types of constraints  Upper limits where the amount used is ≤ the amount of a resource  Lower limits where the amount used is ≥ the amount of the resource  Equalities where the amount used is = the amount of the resource
  • 17.
    B - 17©2011 Pearson Education, Inc. publishing as Prentice Hall Formulating LP Problems Second Constraint: 2X1 + 1X2 ≤ 100 (hours of assembly time) Assembly time available Assembly time used is ≤ First Constraint: 4X1 + 3X2 ≤ 240 (hours of electronic time) Electronic time available Electronic time used is ≤
  • 18.
    B - 18©2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution  Can be used when there are two decision variables 1. Plot the constraint equations at their limits by converting each equation to an equality 2. Identify the feasible solution space 3. Create an iso-profit line based on the objective function 4. Move this line outwards until the optimal point is identified
  • 19.
    B - 19©2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Assembly (Constraint B) Electronics (Constraint A) Feasible region Figure B.3
  • 20.
    B - 20©2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Assembly (Constraint B) Electronics (Constraint A) Feasible region Figure B.3 Iso-Profit Line Solution Method Choose a possible value for the objective function $210 = 7X1 + 5X2 Solve for the axis intercepts of the function and plot the line X2 = 42 X1 = 30
  • 21.
    B - 21©2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Figure B.4 (0, 42) (30, 0) $210 = $7X1 + $5X2
  • 22.
    B - 22©2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Figure B.5 $210 = $7X1 + $5X2 $420 = $7X1 + $5X2 $350 = $7X1 + $5X2 $280 = $7X1 + $5X2
  • 23.
    B - 23©2011 Pearson Education, Inc. publishing as Prentice Hall Graphical Solution 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Figure B.6 $410 = $7X1 + $5X2 Maximum profit line Optimal solution point (X1 = 30, X2 = 40)
  • 24.
    B - 24©2011 Pearson Education, Inc. publishing as Prentice Hall 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 NumberofBlueBerrys Number of x-pods X1 X2 Corner-Point Method Figure B.7 1 2 3 4
  • 25.
    B - 25©2011 Pearson Education, Inc. publishing as Prentice Hall Corner-Point Method  The optimal value will always be at a corner point  Find the objective function value at each corner point and choose the one with the highest profit Point 1 : (X1 = 0, X2 = 0) Profit $7(0) + $5(0) = $0 Point 2 : (X1 = 0, X2 = 80) Profit $7(0) + $5(80) = $400 Point 4 : (X1 = 50, X2 = 0) Profit $7(50) + $5(0) = $350
  • 26.
    B - 26©2011 Pearson Education, Inc. publishing as Prentice Hall Corner-Point Method  The optimal value will always be at a corner point  Find the objective function value at each corner point and choose the one with the highest profit Point 1 : (X1 = 0, X2 = 0) Profit $7(0) + $5(0) = $0 Point 2 : (X1 = 0, X2 = 80) Profit $7(0) + $5(80) = $400 Point 4 : (X1 = 50, X2 = 0) Profit $7(50) + $5(0) = $350 Solve for the intersection of two constraints 2X1 + 1X2 ≤ 100 (assembly time) 4X1 + 3X2 ≤ 240 (electronics time) 4X1 + 3X2 = 240 - 4X1 - 2X2 = -200 + 1X2 = 40 4X1 + 3(40) = 240 4X1 + 120 = 240 X1 = 30
  • 27.
    B - 27©2011 Pearson Education, Inc. publishing as Prentice Hall Corner-Point Method  The optimal value will always be at a corner point  Find the objective function value at each corner point and choose the one with the highest profit Point 1 : (X1 = 0, X2 = 0) Profit $7(0) + $5(0) = $0 Point 2 : (X1 = 0, X2 = 80) Profit $7(0) + $5(80) = $400 Point 4 : (X1 = 50, X2 = 0) Profit $7(50) + $5(0) = $350 Point 3 : (X1 = 30, X2 = 40) Profit $7(30) + $5(40) = $410
  • 28.
    B - 28©2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Analysis  How sensitive the results are to parameter changes  Change in the value of coefficients  Change in a right-hand-side value of a constraint  Trial-and-error approach  Analytic postoptimality method
  • 29.
    B - 29©2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Report Program B.1
  • 30.
    B - 30©2011 Pearson Education, Inc. publishing as Prentice Hall Changes in Resources  The right-hand-side values of constraint equations may change as resource availability changes  The shadow price of a constraint is the change in the value of the objective function resulting from a one-unit change in the right-hand- side value of the constraint
  • 31.
    B - 31©2011 Pearson Education, Inc. publishing as Prentice Hall Changes in Resources  Shadow prices are often explained as answering the question “How much would you pay for one additional unit of a resource?”  Shadow prices are only valid over a particular range of changes in right- hand-side values  Sensitivity reports provide the upper and lower limits of this range
  • 32.
    B - 32©2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Analysis – 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 X1 X2 Figure B.8 (a) Changed assembly constraint from 2X1 + 1X2 = 100 to 2X1 + 1X2 = 110 Electronics constraint is unchanged Corner point 3 is still optimal, but values at this point are now X1 = 45, X2 = 20, with a profit = $415 1 2 3 4
  • 33.
    B - 33©2011 Pearson Education, Inc. publishing as Prentice Hall Sensitivity Analysis – 100 – – 80 – – 60 – – 40 – – 20 – – –| | | | | | | | | | | 0 20 40 60 80 100 X1 X2 Figure B.8 (b) Changed assembly constraint from 2X1 + 1X2 = 100 to 2X1 + 1X2 = 90 Electronics constraint is unchanged Corner point 3 is still optimal, but values at this point are now X1 = 15, X2 = 60, with a profit = $405 1 2 3 4
  • 34.
    B - 34©2011 Pearson Education, Inc. publishing as Prentice Hall Changes in the Objective Function  A change in the coefficients in the objective function may cause a different corner point to become the optimal solution  The sensitivity report shows how much objective function coefficients may change without changing the optimal solution point
  • 35.
    B - 35©2011 Pearson Education, Inc. publishing as Prentice Hall Solving Minimization Problems  Formulated and solved in much the same way as maximization problems  In the graphical approach an iso- cost line is used  The objective is to move the iso- cost line inwards until it reaches the lowest cost corner point
  • 36.
    B - 36©2011 Pearson Education, Inc. publishing as Prentice Hall Minimization Example X1 = number of tons of black-and-white picture chemical produced X2 = number of tons of color picture chemical produced Minimize total cost = 2,500X1 + 3,000X2 Subject to: X1 ≥ 30 tons of black-and-white chemical X2 ≥ 20 tons of color chemical X1 + X2 ≥ 60 tons total X1, X2 ≥ $0 nonnegativity requirements
  • 37.
    B - 37©2011 Pearson Education, Inc. publishing as Prentice Hall Minimization Example Table B.9 60 – 50 – 40 – 30 – 20 – 10 – –| | | | | | | 0 10 20 30 40 50 60 X1 X2 Feasible region X1 = 30 X2 = 20 X1 + X2 = 60 b a
  • 38.
    B - 38©2011 Pearson Education, Inc. publishing as Prentice Hall Minimization Example Total cost at a = 2,500X1 + 3,000X2 = 2,500 (40) + 3,000(20) = $160,000 Total cost at b = 2,500X1 + 3,000X2 = 2,500 (30) + 3,000(30) = $165,000 Lowest total cost is at point a
  • 39.
    B - 39©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications Production-Mix Example Department Product Wiring Drilling Assembly Inspection Unit Profit XJ201 .5 3 2 .5 $ 9 XM897 1.5 1 4 1.0 $12 TR29 1.5 2 1 .5 $15 BR788 1.0 3 2 .5 $11 Capacity Minimum Department (in hours) Product Production Level Wiring 1,500 XJ201 150 Drilling 2,350 XM897 100 Assembly 2,600 TR29 300 Inspection 1,200 BR788 400
  • 40.
    B - 40©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications X1 = number of units of XJ201 produced X2 = number of units of XM897 produced X3 = number of units of TR29 produced X4 = number of units of BR788 produced Maximize profit = 9X1 + 12X2 + 15X3 + 11X4 subject to .5X1 + 1.5X2 + 1.5X3 + 1X4 ≤ 1,500 hours of wiring 3X1 + 1X2 + 2X3 + 3X4 ≤ 2,350 hours of drilling 2X1 + 4X2 + 1X3 + 2X4 ≤ 2,600 hours of assembly .5X1 + 1X2 + .5X3 + .5X4 ≤ 1,200 hours of inspection X1 ≥ 150 units of XJ201 X2 ≥ 100 units of XM897 X3 ≥ 300 units of TR29 X4 ≥ 400 units of BR788
  • 41.
    B - 41©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications Diet Problem Example A 3 oz 2 oz 4 oz B 2 oz 3 oz 1 oz C 1 oz 0 oz 2 oz D 6 oz 8 oz 4 oz Feed Product Stock X Stock Y Stock Z
  • 42.
    B - 42©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications X1 = number of pounds of stock X purchased per cow each month X2 = number of pounds of stock Y purchased per cow each month X3 = number of pounds of stock Z purchased per cow each month Minimize cost = .02X1 + .04X2 + .025X3 Ingredient A requirement: 3X1 + 2X2 + 4X3 ≥ 64 Ingredient B requirement: 2X1 + 3X2 + 1X3 ≥ 80 Ingredient C requirement: 1X1 + 0X2 + 2X3 ≥ 16 Ingredient D requirement: 6X1 + 8X2 + 4X3 ≥ 128 Stock Z limitation: X3 ≤ 80 X1, X2, X3 ≥ 0 Cheapest solution is to purchase 40 pounds of grain X at a cost of $0.80 per cow
  • 43.
    B - 43©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications Labor Scheduling Example F = Full-time tellers P1 = Part-time tellers starting at 9 AM (leaving at 1 PM) P2 = Part-time tellers starting at 10 AM (leaving at 2 PM) P3 = Part-time tellers starting at 11 AM (leaving at 3 PM) P4 = Part-time tellers starting at noon (leaving at 4 PM) P5 = Part-time tellers starting at 1 PM (leaving at 5 PM) Time Number of Time Number of Period Tellers Required Period Tellers Required 9 AM - 10 AM 10 1 PM - 2 PM 18 10 AM - 11 AM 12 2 PM - 3 PM 17 11 AM - Noon 14 3 PM - 4 PM 15 Noon - 1 PM 16 4 PM - 5 PM 10
  • 44.
    B - 44©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications = $75F + $24(P1 + P2 + P3 + P4 + P5) Minimize total daily manpower cost F + P1 ≥ 10 (9 AM - 10 AM needs) F + P1 + P2 ≥ 12 (10 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 ≥ 14 (11 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 + P4 ≥ 16 (noon - 1 PM needs) F + P2 + P3 + P4 + P5 ≥ 18 (1 PM - 2 PM needs) F + P3 + P4 + P5 ≥ 17 (2 PM - 3 PM needs) F + P4 + P5 ≥ 15 (3 PM - 7 PM needs) F + P5 ≥ 10 (4 PM - 5 PM needs) F ≤ 12 4(P1 + P2 + P3 + P4 + P5) ≤ .50(10 + 12 + 14 + 16 + 18 + 17 + 15 + 10)
  • 45.
    B - 45©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications = $75F + $24(P1 + P2 + P3 + P4 + P5) Minimize total daily manpower cost F + P1 ≥ 10 (9 AM - 10 AM needs) F + P1 + P2 ≥ 12 (10 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 ≥ 14 (11 AM - 11 AM needs) 1/2 F + P1 + P2 + P3 + P4 ≥ 16 (noon - 1 PM needs) F + P2 + P3 + P4 + P5 ≥ 18 (1 PM - 2 PM needs) F + P3 + P4 + P5 ≥ 17 (2 PM - 3 PM needs) F + P4 + P5 ≥ 15 (3 PM - 7 PM needs) F + P5 ≥ 10 (4 PM - 5 PM needs) F ≤ 12 4(P1 + P2 + P3 + P4 + P5) ≤ .50(112) F, P1, P2, P3, P4, P5 ≥ 0
  • 46.
    B - 46©2011 Pearson Education, Inc. publishing as Prentice Hall LP Applications There are two alternate optimal solutions to this problem but both will cost $1,086 per day F = 10 F = 10 P1 = 0 P1 = 6 P2 = 7 P2 = 1 P3 = 2 P3 = 2 P4 = 2 P4 = 2 P5 = 3 P5 = 3 First Second Solution Solution
  • 47.
    B - 47©2011 Pearson Education, Inc. publishing as Prentice Hall The Simplex Method  Real world problems are too complex to be solved using the graphical method  The simplex method is an algorithm for solving more complex problems  Developed by George Dantzig in the late 1940s  Most computer-based LP packages use the simplex method
  • 48.
    B - 48©2011 Pearson Education, Inc. publishing as Prentice Hall All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printed in the United States of America.