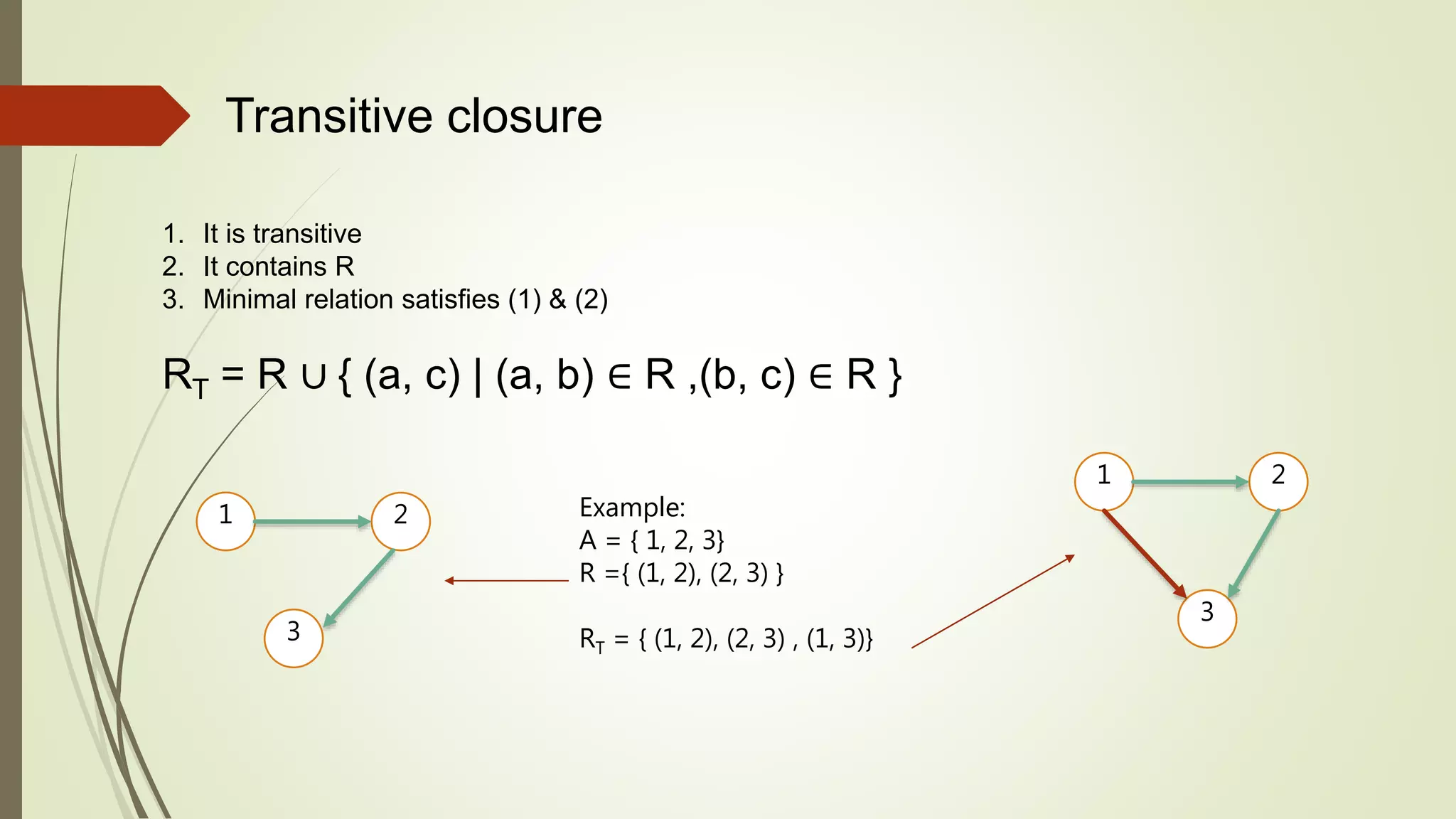
The presentation discusses finding the transitive closure of a graph using Warshall's algorithm, presented by Md. Safayet Hossain. It explains the concept of transitive closure, provides examples, and details the algorithm's process, including the time and space complexities. The final transitive closure matrix is displayed, highlighting the method's efficiency.

1. Welcome
to
My presentation

2. Find Transitive Closure Using Warshall’s Algorithm
Md. Safayet Hossain
M.Sc student of CSE department , KUET.

3. 1. It is transitive
2. It contains R
3. Minimal relation satisfies (1) & (2)
RT = R ∪ { (a, c) | (a, b) ∈ R ,(b, c) ∈ R }
Example:
A = { 1, 2, 3}
R ={ (1, 2), (2, 3) }
RT = { (1, 2), (2, 3) , (1, 3)}
Transitive closure
1 2
3
1 2
3

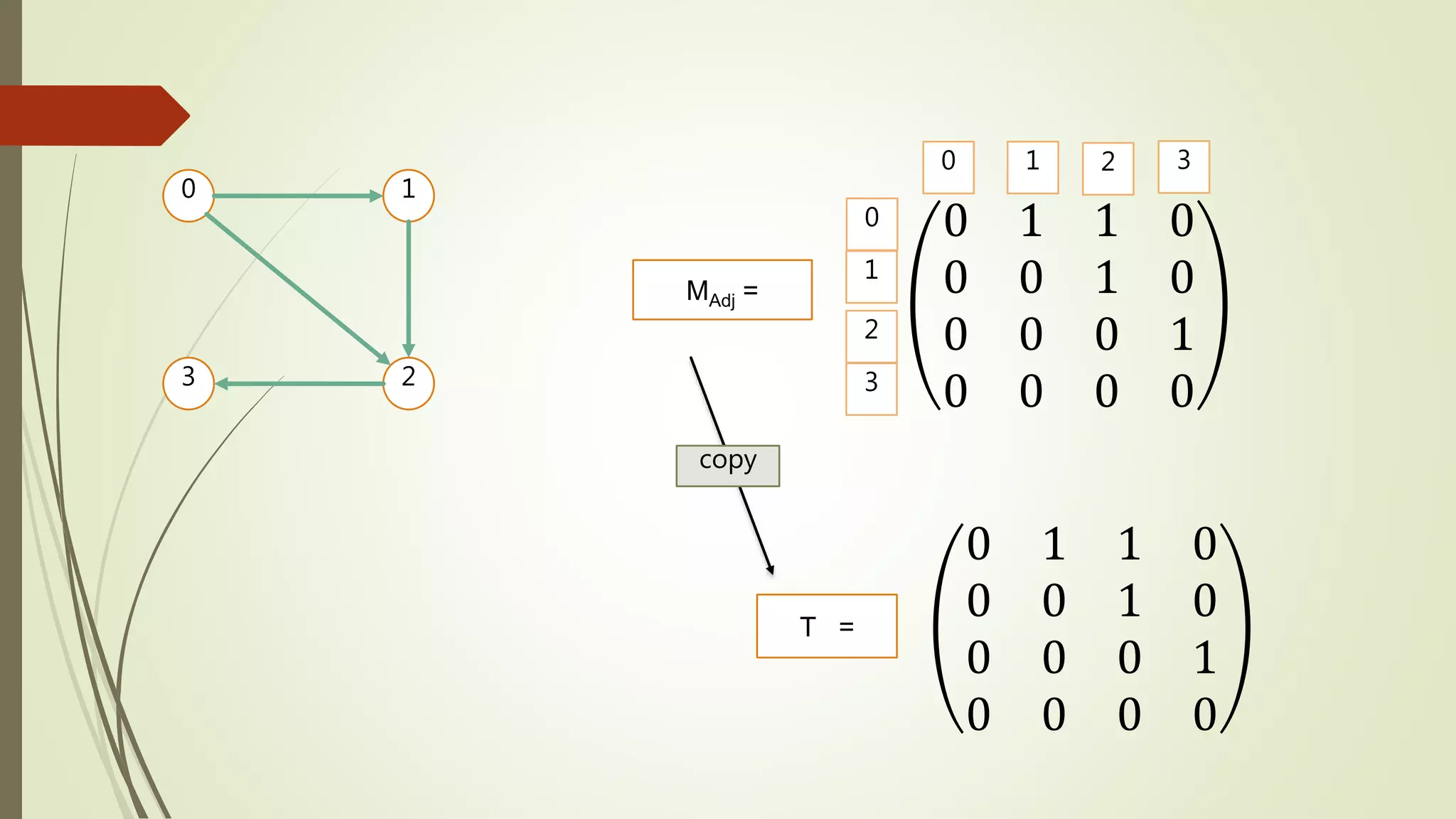
4. Input: Input the given graph as adjacency matrix
Output: Transitive Closure matrix.
Begin
copy the adjacency matrix into another matrix named T
for any vertex k in the graph, do
for each vertex i in the graph, do
for each vertex j in the graph, do
T [ i, j] = T [i, j] OR (T [ i, k]) AND T [ k, j])
done
done
done
Display the T
End
Algorithm to find transitive closure using Warshall’s algorithm

5. 0 1
23
0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
MAdj =
0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
0 1 2 3
0
1
2
3
copy

6. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || ( T[i][k] && T[k][j] );
T[0][0] = T[0][0] || ( T[0][0] && T[0][0] );
}
}
}
0
k =0
i =0
j = 0
T =
Transitive matrix when k = 0

7. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[0][1] = T[0][1] || (T[0][0] && T[0][1]);
}
}
}
0 1
k =0
i =0
j = 1
T =
Transitive matrix when k = 0

8. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[0][2] = T[0][2] || (T[0][0] && T[0][2]);
}
}
}
0 1 1
k =0
i =0
j = 2
T =
Transitive matrix when k = 0

9. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[0][3] = T[0][3] || (T[0][0] && T[0][3]);
}
}
}
0 1 1 0
k =0
i =0
j = 3
T =
Transitive matrix when k = 0

10. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[3][3] = T[3][3] || (T[3][0] && T[0][3]);
}
}
}
0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
k =0
i =3
j = 3
T =
Transitive matrix when k = 0

11. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[3][3] = T[3][3] || (T[3][0] && T[0][3]);
}
}
}
0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
k =1
i =3
j = 3
T =
Transitive matrix when k = 1

12. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[0][3] = T[0][3] || (T[0][2] && T[2][3]);
}
}
}
0 1 1 1
0 0 1 0
0 0 0 1
0 0 0 0
k =2
i =0
j = 3
T =
Transitive matrix when k = 2

13. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[1][3] = T[1][3] || (T[1][2] && T[2][3]);
}
}
}
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
k =2
i =1
j = 3
T =
Transitive matrix when k = 2

14. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[3][3] = T[3][3] || (T[3][2] && T[2][3]);
}
}
}
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
k =2
i =3
j = 3
T =
Transitive matrix when k = 2

15. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
//T[i][j] = T[i][j] || (T[i][k] && T[k][j]);
T[3][3] = T[3][3] || (T[3][3] && T[3][3]);
}
}
}
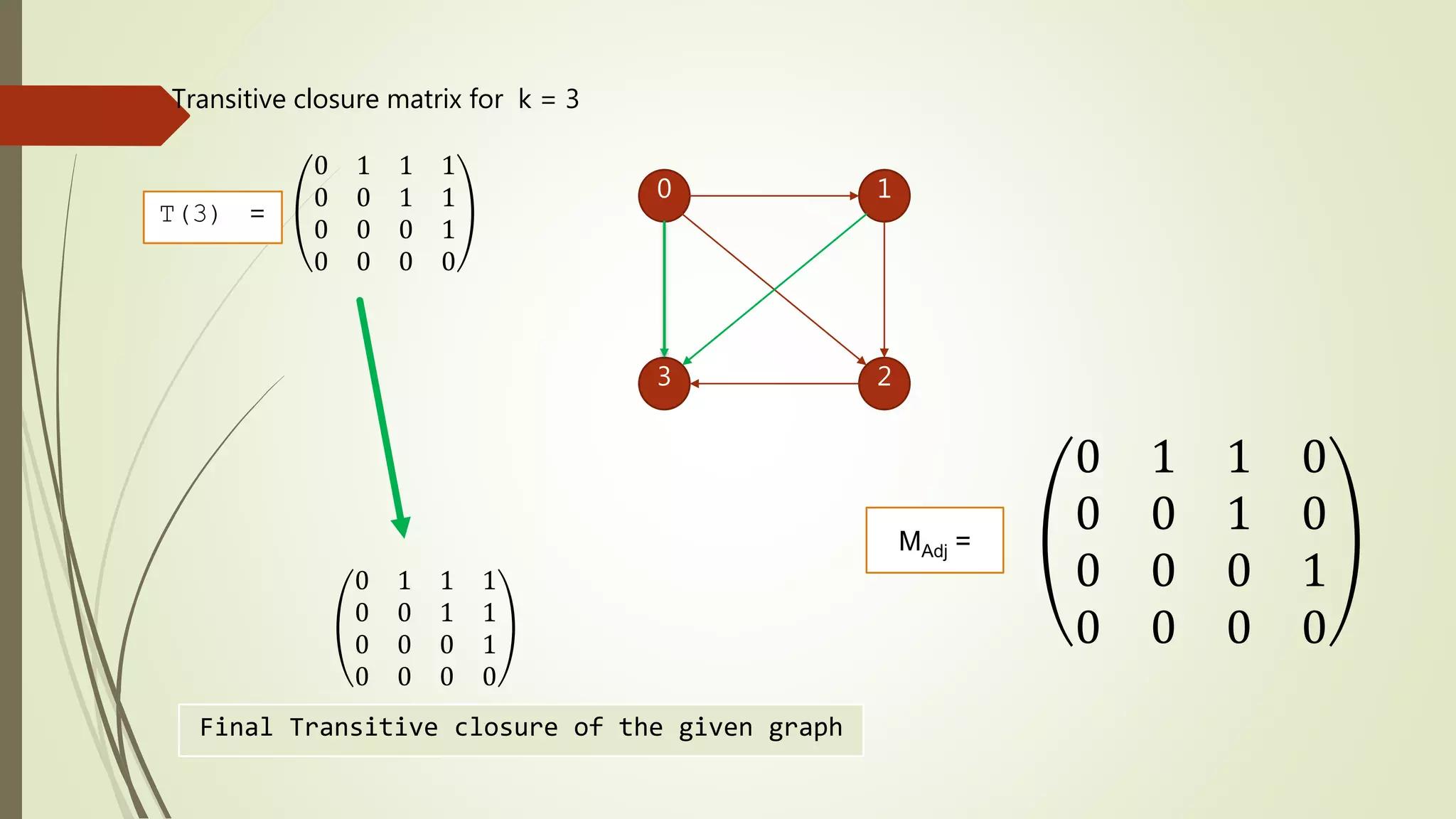
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
k =3
i =3
j = 3
T =
Transitive matrix when k = 3

16. 0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
T(3) =
0 1
23
Final Transitive closure of the given graph
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
Transitive closure matrix for k = 3
0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
MAdj =

17. 0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
T =
0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
0 1 1 0
0 0 1 0
0 0 0 1
0 0 0 0
Transitive closure matrix for k=0
Transitive closure matrix for k=1
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
Transitive closure matrix for k=2
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
Transitive closure matrix for k=3
O(n2)
O(n2)
O(n2)
O(n2)
Time complexity = n * O(n2)
= O(n3)
Space complexity = n * O(n2)
= O(n3)
T =
T =
T =
T =
Time & space Complexity

18. Thank You