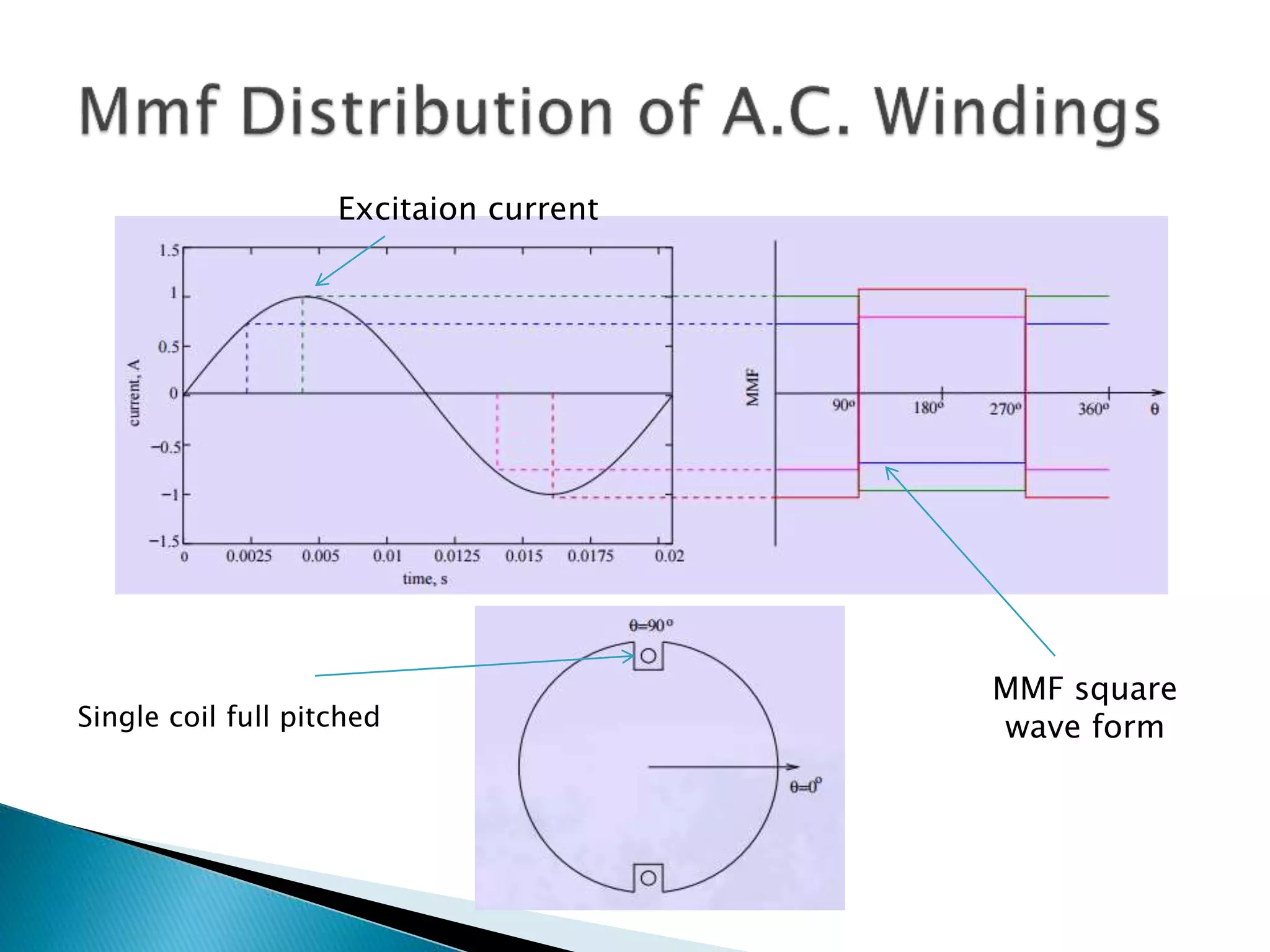
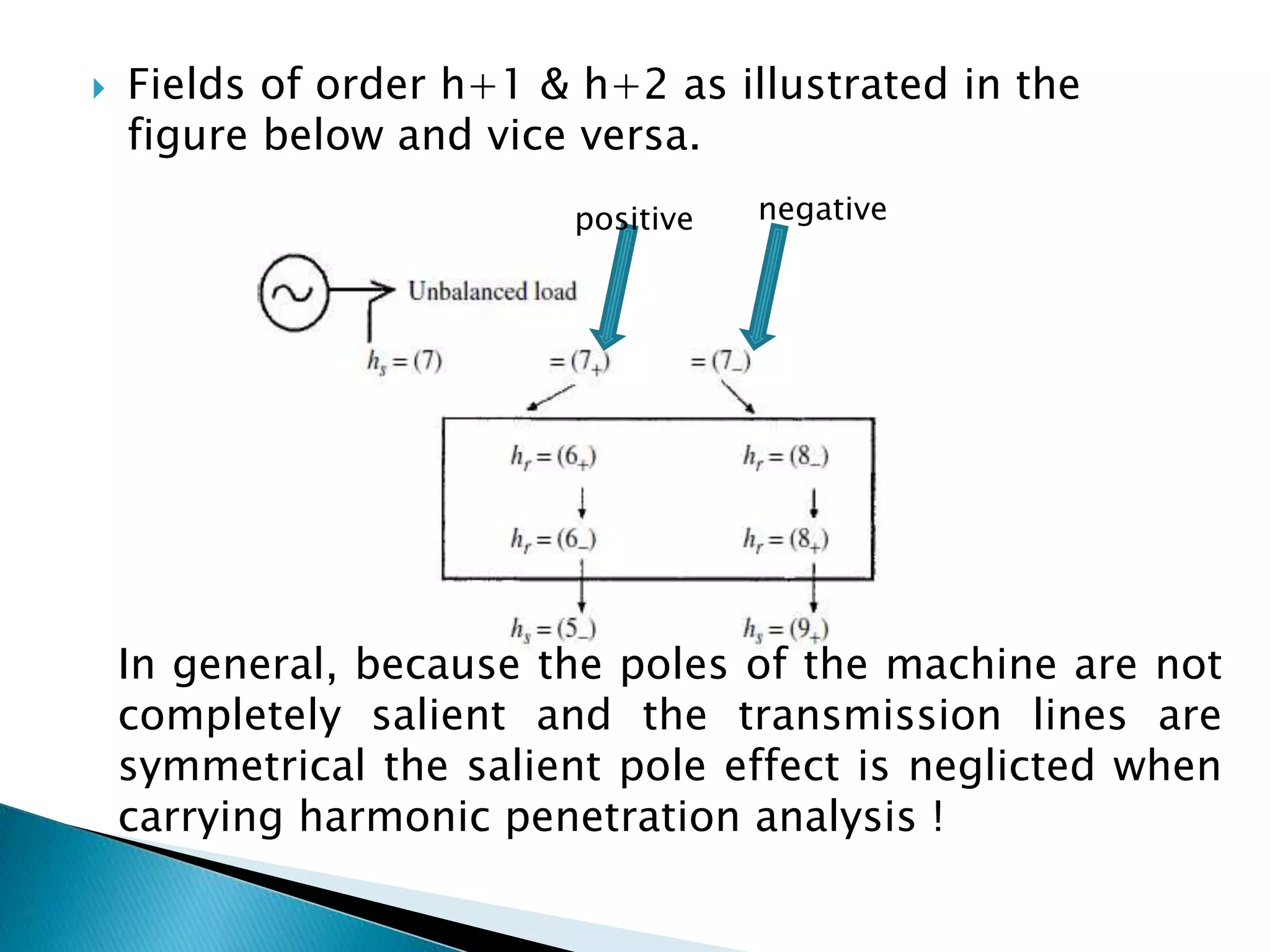
This document discusses harmonics in rotating electrical machines. It explains that the magnetic field produced by windings or slots can be expressed as the sum of the fundamental and higher frequency harmonic components. These harmonics are caused by the non-sinusoidal nature of the magnetic field and can produce unwanted voltages. The magnitudes of the harmonic voltages depend on factors like the coil span and winding configuration, which can be designed to reduce specific harmonics. Harmonics can also be generated through negative and positive sequence currents interacting with the rotor magnetic field.

1. Harmonics in rotating machines

2. Excitaion current
MMF square
wave formSingle coil full pitched

3.  The square wave of the MMF can be
expressed as:
2 2 2 1 2 1 2
( ) sin( ) sin( ) sin(3 ) sin(5 ) ...
3 5
IN x x x
F x t
T T T
  


 
    
 
Where (ɪ) is the (rms) value of the excitation
current, (ω) is the excitation frequency, (T) is
the period of the square mmf. this equation
can be reduced to:
1
2 2 1 2
( ) sin( ) sin( ),
n
IN x
F x t n nisodd
n T


 
 

4.  In practice, windings are distributed spatially
in g slots per pole per phase of the machine.
 In a three phase machine, currents are
displaced by an angle of 120 degrees and the
windings of the machine are also displaced
spatially by 120 degrees. The MMF of each
phase can be expressed by:

5. 1
1
2
1
3
1
2 2 2
( ) sin( ) sin( )
2 2 2 2 2
( ) sin( ) sin( ( )
3 3
2 2 4 2 4
( ) sin( ) sin( ( )
3 3
sin
2
, 3 ,
sin( )
2
dn
n
dn
n
dn
n
dn
kIN x
F x g t n
n T
kIN x
F x g t n
n T
kIN x
F x g t n
n T
n
m
k m phase and n is odd
n
g
mg



  


  








  
  
 
 
  




6.  The total or resultant of the three phase MMF
will result in the form:
5 7
1
3 2 2 2 2
( ) cos( ) cos(5 ) cos(7 ) ...
5 7
d d
d
k kIN x x x
F x g k t t t
T T T
  
  

 
       
 
Fundamental
Fifth
Harmonic
Seventh harmonic

7.  In a machine with mg slots per pole as shown in
figure below; the permeance in the air gap and
the resultant flux density can be given by:
2
1 2sin(2 )
2{ } sin( )r
x
P A A mg
T
xB P B
T


 
 Resultant MMF due
to harmonics of
slots

8.  Resultant B can be divided into a sum of
fundamental and higher frequancy harmonics
as:
1 2
2
1
2 2 2
sin( ) sin( )sin(2 )
2 2 2
sin( ) cos (2 1) cos (2 1)
2
r
r
x x x
B A B A B mg
T T T
A Bx x x
B A B mg mg
T T T
  
  
 
    
        
    
Fundament
al
Harmonics
Which shows that slots give rise the
harmonics 2 1mg 

9.  The flux in the field system is never distributed
perfectly sinusoidally around the air gap in the
machine. therefor, in a salient pole machine the
field distribution can be expressed by:
 Which can be seen such that the machine is having
2P poles generating fundamentals, 6P poles
generating 3rd harmonic, 10P pole generating 5th
harmonic..etc.
 The EMF can also be expressed by:
1 3 5
2 2 2
( ) sin sin 3 sin 5 ...
x x x
F x F F F
T T T
       
        
     
1 3 5( ) sin( ) sin(3 ) sin(5 ) ...E t E t E t E t     

10.  The magnitudes of the emf harmonics given above
are function of the harmonic flux, electrical phase
spread per winding, coil span and interface
connection. By suitable choice of (Kd) and (ks) for
each harmonic order; harmonic emf’s can be
effectively reduced. These factors for each
harmonic order can be given by:
 
sin
2
sin
2
cos
2
dn
sn
ng
k
n
g
nk



 
 
 
 
 
 

As an example, to eliminate the third harmonics it is
enough to choose ks3=0 in the design of a synchronous
generator.

11.  The flux produced by negative sequence stator current
can be divided into two counter rotating components
that induce two Emf in the stator. One of them negative
sequence at the fundamental, the other positive
sequence at the third harmonic. By consequence, the
third harmonic induced emf will produce also two
counter rotating field components that will induce 5th
harmonic. By generalisation, 7th , 9th, etc of harmonic
orders will be generated.
 The same way if the positive sequence stator current
contains a harmonic of order h and positive sequence,
the rotor flux will include two opposite rotating fields
of order h-1. these fields will induce voltages of order h
(positive sequence) and h-2 (negative sequence). The
negative sequence current h will also produce fields

12.  Fields of order h+1 & h+2 as illustrated in the
figure below and vice versa.
negative
In general, because the poles of the machine are not
completely salient and the transmission lines are
symmetrical the salient pole effect is neglicted when
carrying harmonic penetration analysis !
positive

13.  As the frequency of the rotor current in an induction
machine is a function of the slip and stator frequency
(FR=s FS); a harmonic of order n of the rotor mmf will
have a wave length of lampda/n and will induce an emf
in the stator with frequency :
Asymmetry in the rotor windings also can produce
harmonics in the stator of an induction machine due
to the presence of positive and negative sequence
currents in the unbalanced rotor.