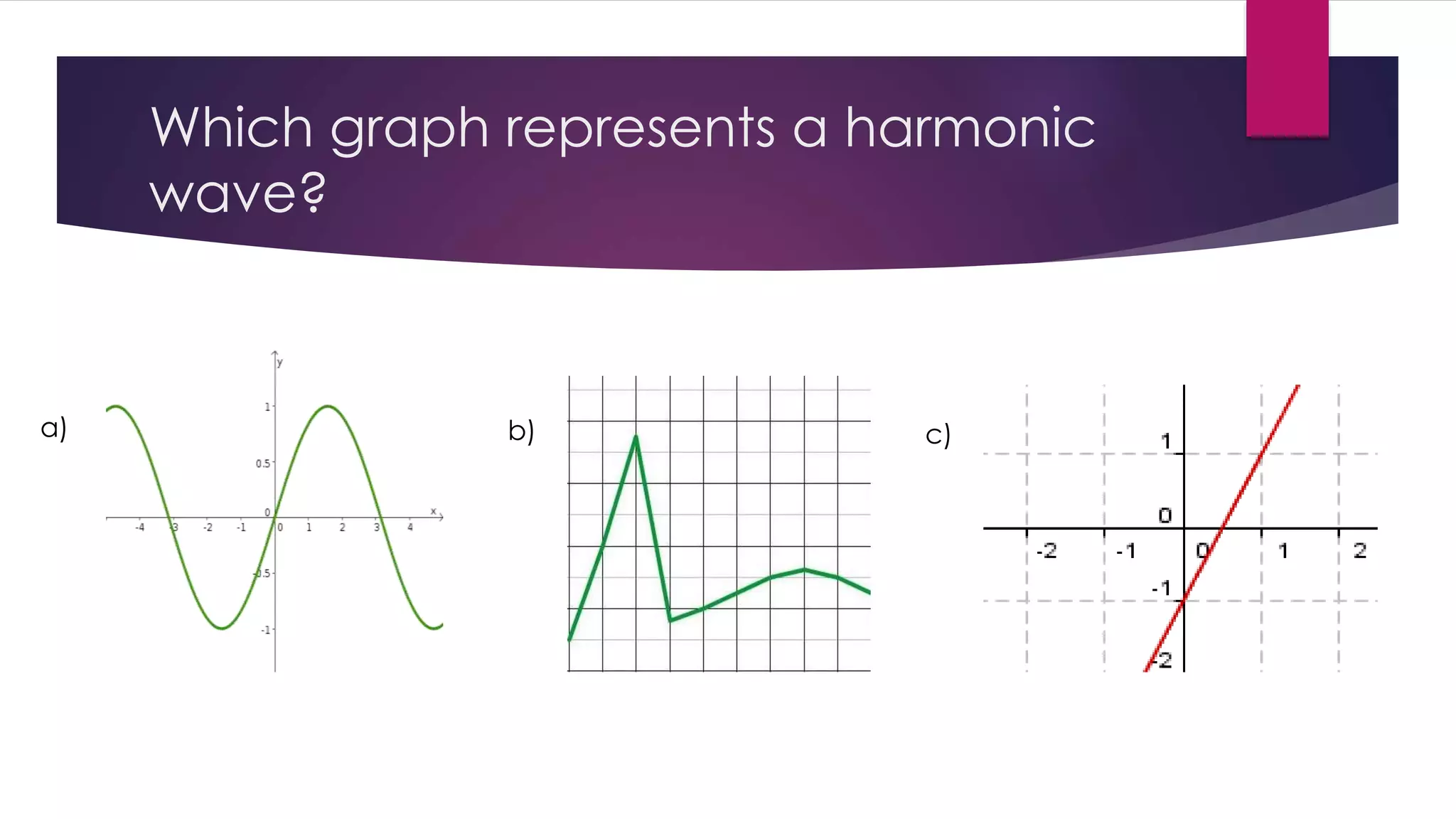
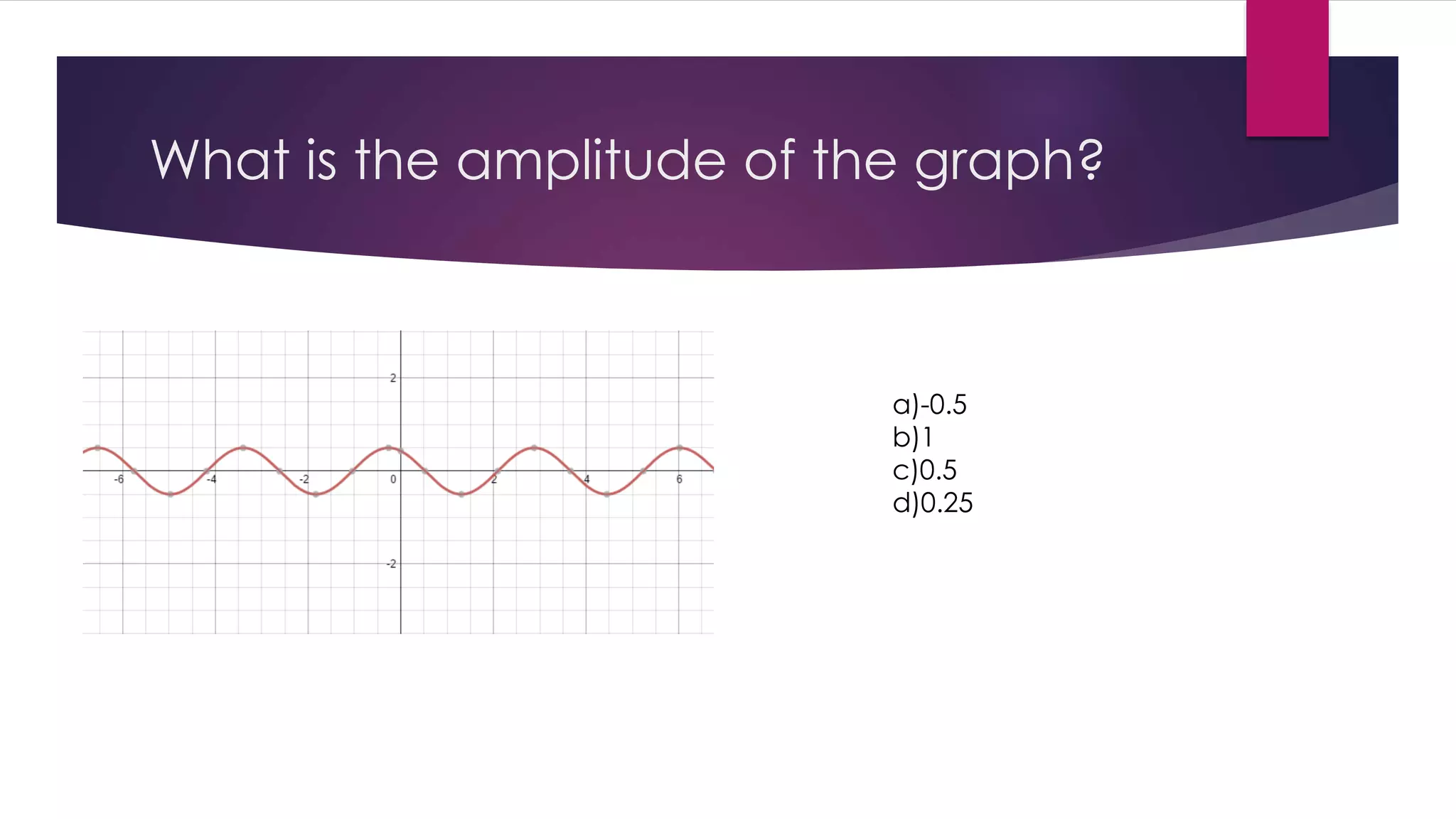
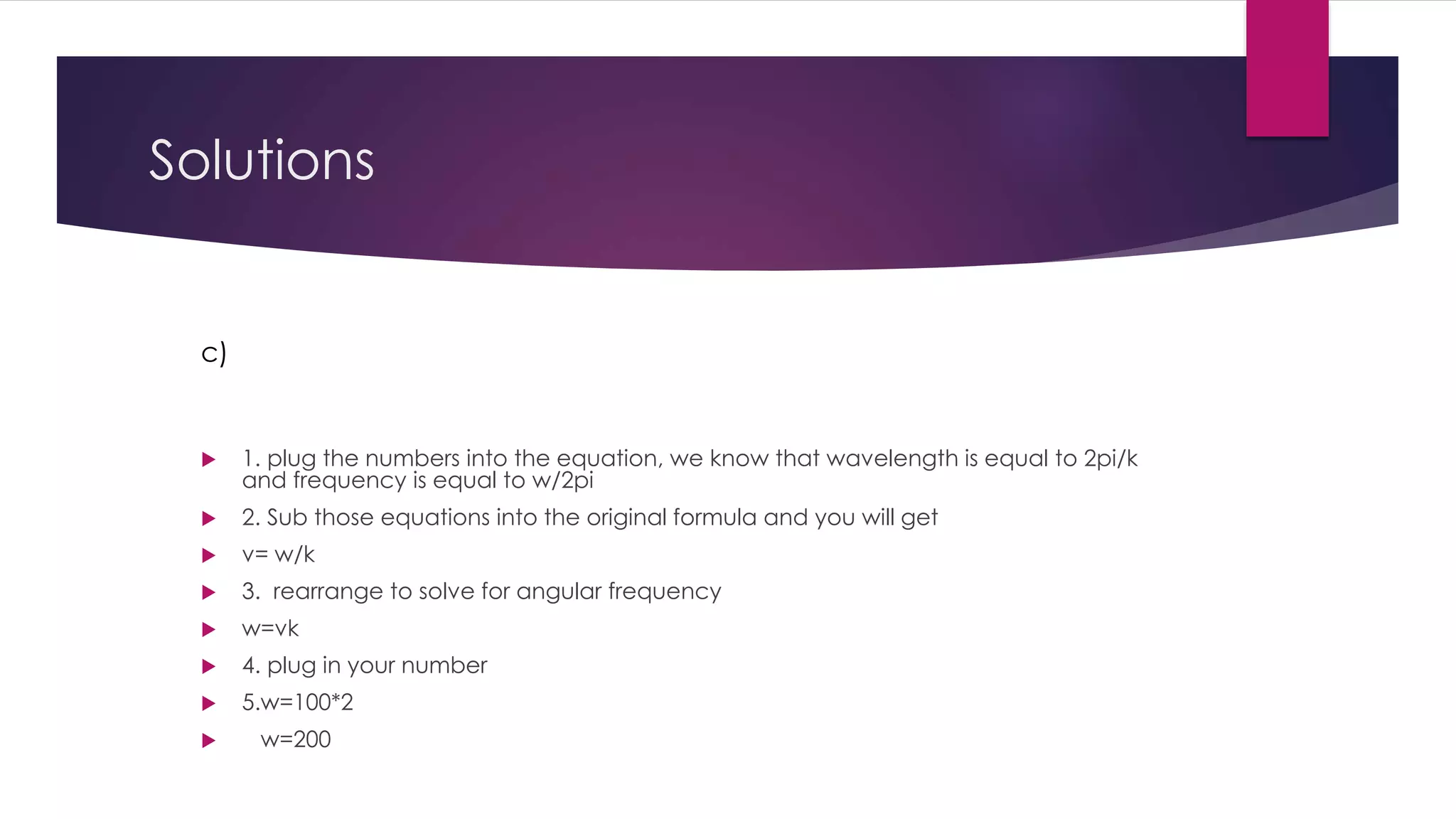
A harmonic wave is a sinusoidal wave that undergoes simple harmonic motion. It has a smooth, repetitive oscillation described by a sine function. The key characteristics of a harmonic wave are its amplitude, wavelength, period, frequency, and phase shift. The speed of a harmonic wave can be calculated by multiplying its wavelength by its frequency. An increase in frequency would cause the velocity of a harmonic wave to increase as well, since these factors are directly correlated.

1. Harmonic Waves
LEARNING OBJECT
LG2- ALISON WU

2. What is a Harmonic Wave?
 If a wave is undergoing harmonic motion it is considered a
harmonic wave. Simple harmonic motion is the type of periodic
motion in which the restoring force is directly proportional to the
displacement
 It is also known as a sinusoidal wave (a sin graph)
 It has a smooth repetitive oscillation

3. Which graph represents a harmonic
wave?
a) b) c)

4. Solution
 A)

5.  Since a harmonic wave is described by a sine (or a cosine) function, its
properties are determined by the amplitude (A), it’s wavelength (λ) and
it’s period (T)

6. Characteristics of a Harmonic wave
 Amplitude: Corresponds to the maximum displacement from the equilibrium
position of any element. Amplitude is always a positive quantity.
 Wavelength: The shortest distance over which a wave shape repeats is called
the wavelength. Represented by the symbol lambda (λ)
 Wave number: the reciprocal of the wavelength
 Period: the time for a particle make one complete cycle T=1/f
 Frequency: the number of wave cycles passing a fixed point of the medium in
one section
 Phase shift (φ) : a horizontal shift by how many units the "starting point" (0,0) of
a standard sine curve, y = sin(x), has moved to the right or left.

7. What is the amplitude of the graph?
a)-0.5
b)1
c)0.5
d)0.25

8. What is the wave number of the
graph?
a)pi
b)pi/2
c)1/2
d)2

9. What is the phase shift?
a)2pi
b)2pi/3
c)pi/3
d)pi

10. Solutions
 1. c) 0.5
 2. d) 2
 3. b)2pi/3

11. Speed of the Wave
 To calculate the speed of the wave you multiply the wavelength of the
graph to the frequency.

12. Find the angular frequency when the
wave has a velocity of 100m/s, a
wave number of 2.
 a) 50
 b) 0
 c) 200
 d) 30

13. Solutions
 1. plug the numbers into the equation, we know that wavelength is equal to 2pi/k
and frequency is equal to w/2pi
 2. Sub those equations into the original formula and you will get
 v= w/k
 3. rearrange to solve for angular frequency
 w=vk
 4. plug in your number
 5.w=100*2
 w=200
c)

14. If the frequency increased what
would happen to the velocity?
 a) it remains constant
 b) it would decrease
 c) it would increase

15. Solution
 C) it would increase
 All three factors are in direct correlation so if the frequency increased the
velocity would increase to.