The document provides an overview of optimization solvers in Python including: - Solvers for scalar, linear, nonlinear, integer programming and multi-objective problems - Examples of unconstrained and constrained optimization problems - Case studies applying solvers to minimize objective functions subject to varying constraints - Techniques for parameter estimation, nonlinear regression, curve fitting and solving systems of ordinary differential equations.

1. Hands on with Optimization solvers in PYTHON
Presentation on
Dr. Kishalay Mitra
Professor, Department of Chemical Engineering
Indian Institute of Technology Hyderabad
kishalay@che.iith.ac.in

2. Indian Institute of Technology Hyderabad
Department of Chemical Engineering
Type Formulation Solver
Scalar minimization min
𝑥
𝑓(𝑥)
such that lb<x<ub (x is a scalar)
fminbound,
minimize_scalar
Unconstrained minimization min
𝑥
𝑓(𝑥) fmin, fmin_powell
Linear programming min
𝑥
𝑓𝑇
𝑥
such that 𝐴. 𝑥 ≤ 𝑏, 𝐴𝑒𝑞. 𝑥 = 𝑏𝑒𝑞, 𝑙𝑏 ≤
𝑥 ≤ 𝑢𝑏
linprog
Mixed integer linear
programming
min
𝑥
𝑓𝑇
𝑥
such that 𝐴. 𝑥 ≤ 𝑏, 𝐴𝑒𝑞. 𝑥 = 𝑏𝑒𝑞, 𝑙𝑏 ≤
𝑥 ≤ 𝑢𝑏
x is integer valued
milp
Constrained minimization min
𝑥
𝑓(𝑥)
such that 𝑐 𝑥 ≤ 0, 𝑐𝑒𝑞 𝑥 = 0,
𝐴. 𝑥 ≤ 𝑏, 𝐴𝑒𝑞. 𝑥 = 𝑏𝑒𝑞, 𝑙𝑏 ≤ 𝑥 ≤ 𝑢𝑏
minimize
Root finding methods min
𝑥
𝑓(𝑥)
such that lb<x<ub
root_scalar, root
Minimization problems : scipy.optimize

3. Department of Chemical Engineering Indian Institute of Technology Hyderabad
Type Formulation Solver
Linear least squares
min
𝑥
1
2
𝑐. 𝑥 − 𝑑 2
m equations, n variables
lsq_linear
Non negative linear least squares
min
𝑥
1
2
𝑐. 𝑥 − 𝑑 2
Such that x≥0
nnls
Nonlinear least squares
min
𝑥
𝐹 𝑥 = min
𝑥
𝑖
𝐹𝑖
2
(𝑥)
such that 𝑙𝑏 ≤ 𝑥 ≤ 𝑢𝑏
least_squares
Nonlinear curve fitting min
𝑥
𝐹 𝑥, 𝑥𝑑𝑎𝑡𝑎 − 𝑦𝑑𝑎𝑡𝑎 2
such that 𝑙𝑏 ≤ 𝑥 ≤ 𝑢𝑏
curve_fit
Least squares (curve fitting) problems: scipy.optimize
Single objective optimization min
𝑥
𝑓(𝑥) GA
Multi objective optimization min
𝑥
𝑓1(𝑥)
m𝑎𝑥
𝑥
𝑓2(𝑥)
NSGA2
Optimization problems: pymoo

4. Optimizer
myfun
Decision
Variables
Objective
function
Unconstrained nonlinear function minimization
Result = optimizer (myfun, x0)
Indian Institute of Technology Hyderabad
Department of Chemical Engineering

5. Case study 1 min
𝑥
𝑓 𝑥 = 12𝑥5
− 45𝑥4
+ 40𝑥3
+ 5
Optimizer
myfun
Decision
Variables
Objective
function
Result = optimizer (myfun, x0)
Unconstrained unbounded nonlinear function minimization
Indian Institute of Technology Hyderabad
Department of Chemical Engineering

6. def f = myfun(x):
f = 12*x^5 - 45*x^4 + 40*x^3 + 5
Case study 1 min
𝑥
𝑓 𝑥 = 12𝑥5
− 45𝑥4
+ 40𝑥3
+ 5
 Result= fmin (myfun, x0)
 Result = fmin_powell (myfun, x0)
Indian Institute of Technology Hyderabad
Department of Chemical Engineering
Result = optimizer (myfun, x0)
Unconstrained unbounded nonlinear function minimization

7. Case study 2 min
𝑥
𝑓 𝑥 = 12𝑥5
− 45𝑥4
+ 40𝑥3
+ 5
Optimizer
myfun
Decision
Variables
Objective
function
Result = optimizer (myfun, 𝑥1, 𝑥2)
such that x ∈ (0.5, 2.5)
Indian Institute of Technology Hyderabad
Department of Chemical Engineering
Unconstrained bounded nonlinear function minimization

8. def f = myfun(x):
f = 12*x^5 - 45*x^4 + 40*x^3 + 5
Case study 2 min
𝑥
𝑓 𝑥 = 12𝑥5
− 45𝑥4
+ 40𝑥3
+ 5
Result = optimizer (myfun, 𝑥1, 𝑥2)
such that x ∈ (0.5, 2.5)
 Result = fminbound (myfun, 𝑥1, 𝑥2)
Indian Institute of Technology Hyderabad
Department of Chemical Engineering
Unconstrained bounded nonlinear function minimization

9. def f = myfun(x):
f = 12*x^5 - 45*x^4 + 40*x^3 + 5
f = -f;
Case study 3 m𝑎𝑥
𝑥
𝑓 𝑥 = 12𝑥5
− 45𝑥4
+ 40𝑥3
+ 5
such that x ∈ (0.5, 2.5)
Indian Institute of Technology Hyderabad
Department of Chemical Engineering
Unconstrained bounded nonlinear function maximization
Result = optimizer (myfun, 𝑥1, 𝑥2)
 Result = fminbound (myfun, 𝑥1, 𝑥2)

10. Case study 4
Root finder
myfun
Variable
Function
value
Result = rootfinder (myfun, x0)
Root finding
min
𝑥,𝑦
𝑓 𝑥, 𝑦 = 3𝑥2
− 6
𝑥0 = 0.2
Indian Institute of Technology Hyderabad
Department of Chemical Engineering
 Result = root_scalar(fun, x0, fprime=fprime)

11. • lsq_linear, nnls, least_squares, curve_fit are the operators used for
solving an overdetermined system of linear equations
• Result = optimize.curve_fit(myfun, 𝑥𝑑𝑎𝑡𝑎, 𝑦𝑑𝑎𝑡𝑎, p0)
lsqcurvefit
myfun
p0 – decision
variables/
Parameters and
𝑥𝑑𝑎𝑡𝑎
𝑦𝑠𝑖𝑚𝑢𝑙𝑎𝑡𝑒𝑑
𝑦𝑑𝑎𝑡𝑎
Indian Institute of Technology Hyderabad
Department of Chemical Engineering
Linear & Nonlinear regression and curve fitting

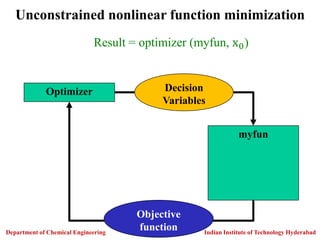
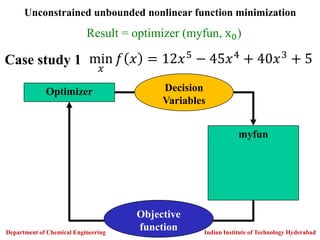
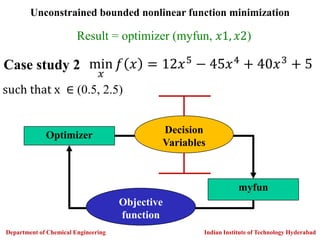
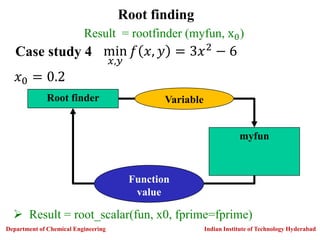
12. Result= optimize.minimize(c=f, x0, constraints, method,
bounds=[lb,ub])
Optimizer
Model
Decision
Variables
Objective and
Constraints
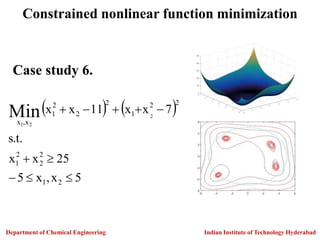
Constrained nonlinear function minimization
Indian Institute of Technology Hyderabad
Department of Chemical Engineering

13. Result= optimize.minimize(c=f, x0, constraints, method,
bounds=[lb,ub])
Constrained nonlinear function minimization
Indian Institute of Technology Hyderabad
Department of Chemical Engineering

14. Case study 5
Indian Institute of Technology Hyderabad
Department of Chemical Engineering
Constrained nonlinear function minimization

15.    
5
x
,
x
5
25
x
x
.
t
.
s
7
x
x
11
x
x
2
1
2
2
2
1
2
2
1
2
2
2
1
x
,
x
2
2
1
Min










Constrained nonlinear function minimization
Case study 6.
Indian Institute of Technology Hyderabad
Department of Chemical Engineering

16. Indian Institute of Technology Hyderabad
Department of Chemical Engineering
𝒎𝒊𝒏 𝒇𝟏 𝒙, 𝒚 = 𝟒𝒙𝟐 + 𝟒𝒚𝟐
𝒎𝒊𝒏 𝒇𝟐 𝒙, 𝒚 = 𝒙 − 𝟓 𝟐
+ 𝒚 − 𝟓 𝟐
𝒈𝟏 𝒙, 𝒚 = 𝒙 − 𝟓 𝟐 + 𝒚 𝟐 ≤ 𝟐𝟓
𝒈𝟐 𝒙, 𝒚 = 𝒙 − 𝟖 𝟐 + 𝒚 + 𝟑 𝟐 ≤ 𝟕. 𝟕
𝟎 ≤ 𝒙 ≤ 𝟓 𝟎 ≤ 𝒚 ≤ 𝟑
Constrained nonlinear Multi objective optimization
Case study 7.

17. Unconstrained nonlinear function minimization
Linear & Nonlinear Regression and Curve Fitting
Case study 8. ODE Solving
First order series reactions happening in an isothermal
batch reactor
0
)
0
(
c
),
t
(
b
k
dt
dc
0
)
0
(
b
),
t
(
b
k
)
t
(
a
k
dt
db
1
)
0
(
a
),
t
(
a
k
dt
da
2
2
1
1








A B C
k1 k2
Solve using solve_ivp
& then perform parameter
estimation using minimize
Indian Institute of Technology Hyderabad
Department of Chemical Engineering

18. Unconstrained nonlinear function minimization
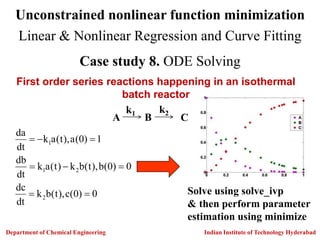
Linear & Nonlinear Regression and Curve Fitting
First order series reactions happening in an isothermal
batch reactor
0
)
0
(
,
0
)
0
(
,
1
)
0
(
)
(
)
(
)
(
)
(
2
2
1
1








c
b
a
t
b
k
dt
dc
t
b
k
t
a
k
dt
db
t
a
k
dt
da
A B C
k1 k2
def my_model(t,y,k):
f =[]
f[0] = -k[0]*y[0]
f[2] = k[0]*y[0]-k[1]*y[1]
f[3] = k[1]*y[1]
return f
Indian Institute of Technology Hyderabad
Department of Chemical Engineering

19. def fun:
ic = [1,0,0]
tspan = [0 0.05 0.1 0.15 0.2 0.3 0.4 0.45 0.56
0.67 0.7 0.75 0.78 0.8 0.9 0.92 1]
k = [6.3,4.23]
sol = solve_ivp(my_model(t,y,k),tspan, ic)
Case study 10. ODE Solving
Indian Institute of Technology Hyderabad
Department of Chemical Engineering