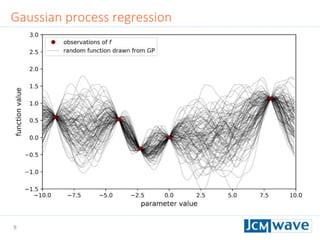
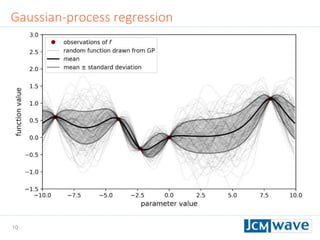
The document describes a machine learning method for efficient design optimization in nano-optics using Gaussian process regression and Bayesian optimization. It discusses how Gaussian process regression can be used to build regression models from expensive black-box functions to enable model-based optimization and integration. Bayesian optimization is then used to iteratively query the black-box function at points of maximum expected improvement to find its minimum. The method can incorporate derivative observations to speed up optimization by providing additional training data for the Gaussian process. Differential evolution is also utilized to efficiently maximize the expected improvement at each iteration. The approach is demonstrated on benchmark optimization problems, showing it outperforms other algorithms like L-BFGS and particle swarm optimization.

1. A machine learning method
for efficient design
optimization in nano-optics

2. 2
Optical behavior of small structures (e.g. scattering in certain
direction) dominated by diffraction, interference and resonance
phenomena
 Full solution of Maxwell’s equation required
 Behavior only known implicitly (black-box
function)
 Computation of solution is time
consuming (expensive
black-box function)
Computational challenges in nano-optics
?

3. 3
Analysis of expensive black-box functions
Typical questions:
• Regression: What is the response 𝑓(𝑥)
for unknown parameter values 𝑥 ?
• Optimization: What are the best
parameter values that lead to a
measured/desired response?
• Integration: What is the average
response?
System response
(requires solution
of Maxwell’s
equations)
k
ω
p1
p2
…
Black-box function
?
Isolated Scatterers Metamaterials Geometry Reconstruction
k, ω

4. 4
Regression models
 Regression models are important
tools to interpolate between
known data points.
 Further, they can be used for
model-based optimization and
numerical integration
(quadrature).

5. 5
+ Accurate and data
efficient
+ Reliable (provides
uncertainties)
+ Interpretable results
‒ Computationally
demanding but not as
much as training neural
networks
Regression models (small selection)
K-nearest neighbors
Linear regression
Support vector machine
Random forest trees
Gaussian process
regression (Kriging)
(Deep) neural networks
[CE Rasmussen, “Gaussian processes in machine learning”. Advanced lectures on machine
learning , Springer (2004)]
[B. Shahriari et al., "Taking the Human Out of the Loop: A Review of Bayesian Optimization“.
Proc. IEEE 104(1), 148 (2016)]
Increasingpredictivepower
andcomputationaldemands

6. 6
Gaussian process regression
How does it work?

7. 7
 Gaussian process (GP): distribution of functions in a continuous domain 𝒳 ⊂ ℝN
 Defined by: mean function 𝜇: 𝒳 → ℝ and covariance function (kernel) 𝑘: 𝒳 × 𝒳 → ℝ
 Training data: 𝑀 known function values 𝑓 𝑥1 , … , 𝑓 𝑥 𝑀 with corresponding
covariance matrix 𝐊 = 𝑘 𝑥𝑖, 𝑥𝑗 𝑖,𝑗
 Random function values at positions 𝐗∗
= (𝑥1
∗
, … , 𝑥 𝑁
∗
):
Multivariate Gaussian random variable 𝐘∗
∼ 𝒩 𝛍, 𝚺 with probability density
𝑝 𝐘∗
=
1
2𝜋 𝑁/2 𝚺 1/2
exp −
1
2
𝐘∗
− 𝛍 𝑇
𝚺−1
𝐘∗
− 𝛍 ,
means, and covariance
𝛍𝑖 = 𝜇(𝑥𝑖
∗
) −
𝑘𝑙
𝑘 𝑥𝑖
∗
, 𝑥 𝑘 𝐊 𝑘𝑙
−1
[𝑓 𝑥𝑙 − 𝜇 𝑥𝑙 ]
𝚺𝑖𝑗 = 𝑘 𝑥𝑖
∗
, 𝑥𝑗
∗
−
𝑘𝑙
𝑘 𝑥𝑖
∗
, 𝑥 𝑘 𝐊 𝑘𝑙
−1
𝑘 𝑥𝑙, 𝑥𝑗
∗
.
 For a proof see:
http://fourier.eng.hmc.edu/e161/lectures/gaussianprocess/node7.html
Gaussian process regression

8. 8
Gaussian process regression

9. 9
In the following we don’t need correlated random vectors of
function values, but just the probability distribution of a
single function value 𝑦 at some 𝑥∗
∈ 𝒳
This is simply a normal distribution 𝑦 ∼ 𝒩( 𝑦, 𝜎2
) with mean
and standard deviation
𝑦 = 𝜇 𝑥∗ +
𝑖𝑗
𝑘 𝑥∗, 𝑥𝑖 𝐊 𝑖𝑗
−1
[𝑓 𝑥𝑗 − 𝜇 𝑥𝑗 ]
𝜎2 = 𝑘 𝑥∗, 𝑥∗ − 𝑖𝑗 𝑘(𝑥∗, 𝑥𝑖) 𝐊 𝑖𝑗
−1
𝑘(𝑥𝑗, 𝑥∗)
Gaussian process regression

10. 10
Gaussian-process regression

11. 11
The mean and covariance function
are usually parametrized as
𝜇 𝑥 = 𝜇0
𝑘 𝑥, 𝑥′ = 𝜎2 𝐶5/2 𝑟 = 𝜎2 1 + 5𝑟 +
5
3
𝑟2 exp − 5𝑟
with 𝑟2 = 𝑖 𝑥𝑖 − 𝑥𝑖
′ 2/𝑙𝑖
2
Take values of 𝜇0, 𝜎, 𝑙𝑖 are maximized w.r.t. the log-likelihood of the
observations:
log 𝑃 𝐘 = −
𝑀
2
log 2𝜋 −
1
2
log 𝐊 −
1
2
𝐘 − 𝛍 𝑇 𝐊−1(𝐘 − 𝛍)
GP hyperparameters
Matern-5/2 function

12. 12
Bayesian optimization
Use Gaussian process
regression to run
optmization or parameter
reconstruction

13. 13
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization

14. 14
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization

15. 15
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization

16. 16
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization

17. 17
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization

18. 18
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization

19. 19
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization

20. 20
Problem: Find parameters 𝑥 ∈ 𝒳 that minimize 𝑓 𝑥 . For the currently known smallest
function value 𝑦 𝑚𝑖𝑛 we define the improvement
𝐼 𝑦 =
0 ∶ 𝑦 ≥ 𝑦 𝑚𝑖𝑛
𝑦 𝑚𝑖𝑛 − 𝑦 ∶ y < 𝑦 𝑚𝑖𝑛
We sample at points of largest expected improvement 𝛼EI(𝑥) = 𝔼 𝐼(𝑦) (analytic function
derived from normal distribution of 𝑦)
Bayesian optimization
For more and more data points in the local
minimum: 𝛼EI 𝑥 → 0.
Hence, we do not get trapped in local
minima, but eventually jump out of them.

21. 21
Utilizing derivatives
The JCMsuite FEM solver can compute also derivatives w.r.t. geometric
parameter, material parameters and others. We can use derivatives to train the
GP because differentiation is a linear operator:
• What is the mean function of the GP for derivative observations?
𝜇 𝐷 𝑥 ≡ 𝔼 𝛻𝑓 𝑥 = 𝛻𝔼 𝑓 𝑥 = 𝛻𝜇 𝑥 = 0
• What is the kernel function between an observation at 𝑥 and a derivative
observation at 𝑥′
?
𝑘 𝐷 𝑥, 𝑥′ ≡ cov 𝑓 𝑥 , 𝛻𝑓 𝑥′ = 𝔼 𝑓 𝑥 − 𝜇 𝑥 𝛻𝑓 𝑥′ − 𝜇 𝐷 𝑥′ = 𝛻𝑥′ 𝑘(𝑥, 𝑥′)
• Analogously, the kernel function between a derivative observation at 𝑥 and a
derivative observation at 𝑥′
is given as
𝑘 𝐷𝐷 𝑥, 𝑥′
≡ cov 𝛻𝑓 𝑥 , 𝛻𝑓 𝑥′
= 𝛻𝑥 𝛻𝑥′ 𝑘(𝑥, 𝑥′)
 We can build a large GP (i.e. a large mean vector and covariance matrix)
containing observations of objective function and its derivatives

22. 22
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.

23. 23
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.

24. 24
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.

25. 25
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.

26. 26
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.

27. 27
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.

28. 28
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.

29. 29
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.
minimum found

30. 30
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.
minimum found

31. 31
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.
minimum found

32. 32
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.
minimum found

33. 33
Utilizing derivatives
without gradient
with gradient
Derivative observations can speed up Bayesian optimization.
minimum found

34. 34
Utilizing derivatives
without gradient
with gradient
minimum found
Derivative observations can speed up Bayesian optimization.

35. 35
Utilizing derivatives
without gradient
with gradient
minimum found
Derivative observations can speed up Bayesian optimization.

36. 36
Utilizing derivatives
without gradient
with gradient
minimum found
Derivative observations can speed up Bayesian optimization.

37. 37
Utilizing derivatives
without gradient
with gradient
minimum found
minimum found
Derivative observations can speed up Bayesian optimization.

38. 38
Solving arg max
𝑥
𝛼EI(𝑥) can be very time consuming.
Bayesian optimization runs inefficiently if the sample computation
takes longer then the objective function calculation (simulation)
We use differential evolution to maximize 𝛼EI(𝑥) and adapt
the effort (i.e. the population size and number of generations)
to the simulation time.
We calculate one sample in advance while the objective
function is evaluated.
See Schneider et al. arXiv:1809.06674 (2019) for details
Making Bayesian optimization time efficient

39. 39
Benchmark
For two benchmark
problems we compare
Bayesian optimization with
other optimization methods

40. 40
Choice of optimization algorithms
We compare the performance of
Bayesian optimization (BO) with
• Local optimization methods
Low-memory Broyden-Fletcher-
Goldfarb-Shanno (L-BFGS-B)
started in parallel from 10
different locations
• Global heuristic optimization
Differential evolution (DE),
Particle swarm optimization (PSO), Covariance matrix
adaptation evolution strategy (CMA-ES)
All optimization methods are run with standard parameters

41. 41
Example 1
Minimization of Rastrigin
function

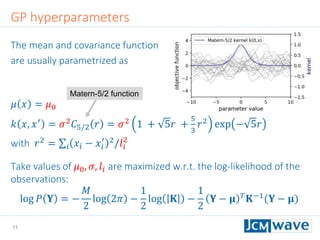
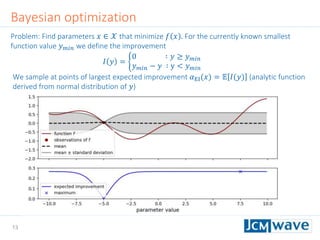
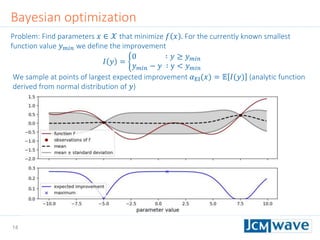
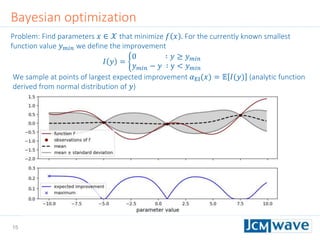
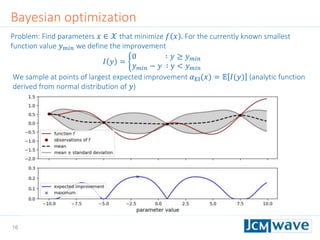
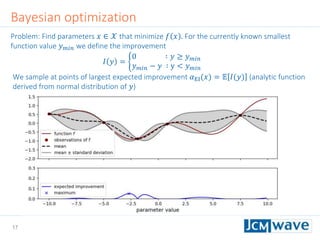
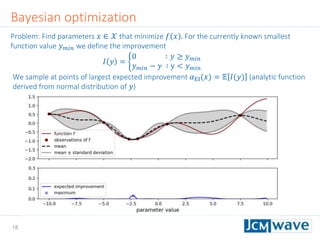
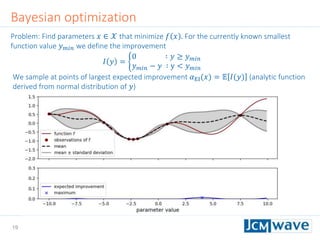
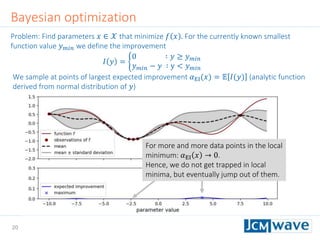
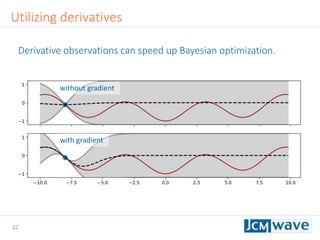
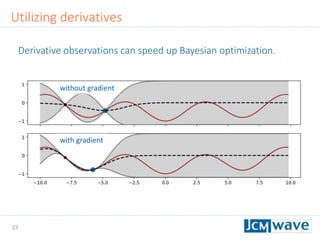
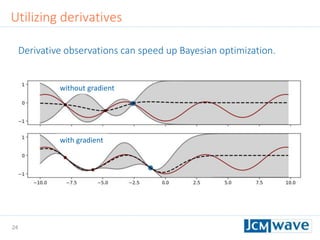
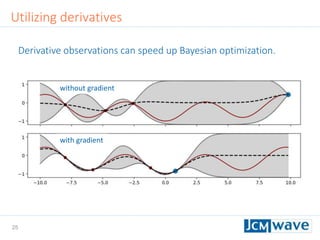
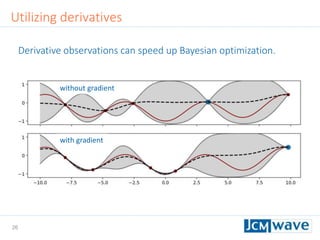
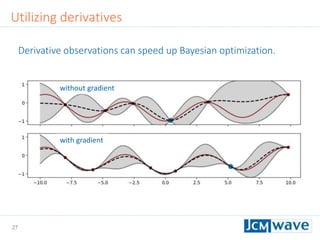
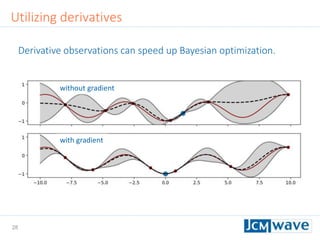
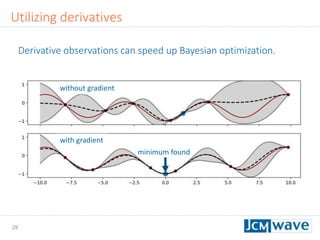
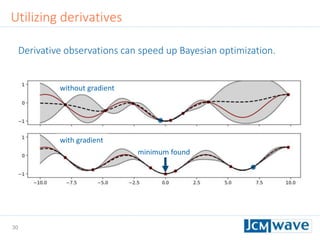
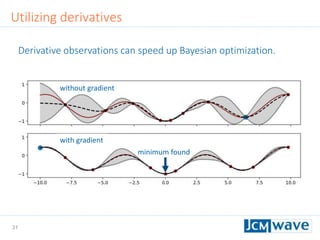
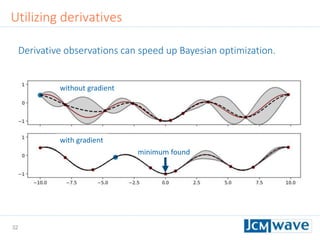
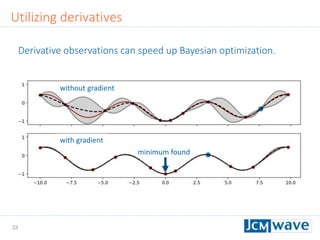
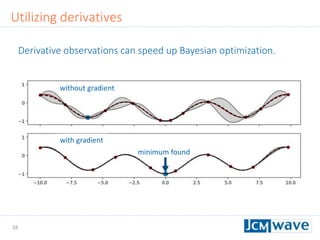
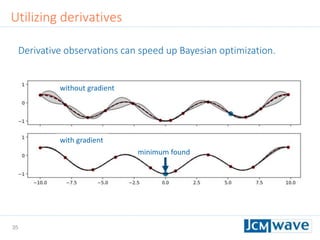
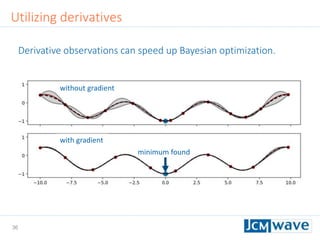
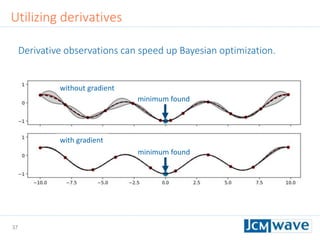
42. 42
Rastrigin function
 Defined on an 𝑛-dimensional domain as 𝑓 𝒙 = 𝐴𝑛 + 𝑖=1
𝑛
[𝑥𝑖
2
− 𝐴 cos(2𝜋𝑥𝑖)] with
𝐴 = 10. We use 𝑛 = 3 and 𝑥𝑖 ∈ [−2.5,2.5].
 Sleeping for 10s during evaluation to make function call “expensive”.
 Parallel minimization with 5 parallel evaluations of 𝑓 𝒙 .
Global minimum 𝑓 𝑚𝑖𝑛 = 0 at 𝒙 = 0

43. 43
Benchmark on Rastrigin function
[Laptop with 2-core Intel Core I7 @ 2.7 GHz]
BO converges significantely faster to the global minimum
Derivative observations improve the convergence
Although more elaborate, BO has no significant computation time
overhead

44. 44
Example 2
Optimization of anti-
reflective metasurface

45. 45
System: Square array of silicon bumps
on silicon substrate. Computation
includes derivatives w.r.t. all 6
geometric parameters.
Optimization task: Find geometric
paramters that suppress reflectivity of
normally incident plane waves between
500 nm and 800 nm.
Run a parallel minimization with 4
parallel evaluations.
Reflection suppression by a metasurface

46. 46
Reflection suppression by a metasurface
Comparison of different global optimization methods
BO more efficient by almost 1 order of magnitude
BO has negligible computation time overhead
[four 10-core Intel Xeon CPUs @ 2.4 GHz]

47. 47
Conclusion
• Bayesian optimization is a highly
efficient method for shape
optimization
• It can incorporate derivative
information if available
• It can be used for very expensive
simulations but also for
fast/parallelized simulations (e.g.
one simulation result every two
seconds)

48. 48
Resources
 Description of FEM software
JCMsuite
 Getting started with JCMsuite
 Tutorial on optimization with
JCMsuite using Matlab®/Python
 Free trial download of JCMsuite