Prolog approximates first-order logic and represents programs as sets of Horn clauses. It performs inference through resolution and searches for solutions through backtracking with unification. Prolog can represent semantic networks and frames to describe relationships between objects, classes, and their properties. It can also perform depth-first search on graphs to find paths between nodes. However, Prolog has limitations in representing higher-order relationships and probabilities.

1. Prolog
The language of logic

2. History
• Kowalski: late 60’s Logician who showed
logical proof can support computation.
• Colmerauer: early 70’s Developed early
version of Prolog for natural language
processing, mainly multiple parses.
• Warren: mid 70’s First version of Prolog
that was efficient.

3. Characteristics
• Prolog approximates first-order logic.
• Every program is a set of Horn clauses.
• Inference is by resolution.
• Search is by backtracking with unification.
• Basic data structure is term or tree.
• Variables are unknowns not locations.
• Prolog does not distinguish between inputs
and outputs. It solves relations/predicates.

4. SWI-Prolog Notes
• Free! Down Loadable
• To load a file:
– consult( ‘C:kiblerprologtest’).
• For help:
– help(predicate-name).
• “ ; “ will give you next solution.
• listing(member) will give definition.

5. Example
• Facts: ()
– likes(john,mary).
– likes(john,X). % Variables begin with capital
• Queries
– ?- likes(X,Y).
– X=john, y=Mary. % hit “;” for more
– ?- likes(X,X).
– X=john.

6. Example
• Rules
– likes(john,X) :- likes(X,wine). % :- = if
– likes(john,X):- female(X), likes(X,john).
• Note: variables are dummy. Standarized apart
• Some Facts:
– likes(bill,wine). female(mary). female(sue).
• Query: ? - likes(john,Y).
– Y = bill ;
– no.

7. • If someone is parent of a person then he/she
is father/mother of him.
• father(sikander, arfa)
• parent(X,Y):-father(X,Y).
• Parent(X,Y):-mother(X.Y).

8. Family
father(a,b).
father(e,d).
mother(c,b).
mother(d,f).
parent(X,Y) :- father(X,Y).
parent(X,Y) :- mother(X,Y).
grandfather(X,Y):- father(X,Z),parent(Z,Y).
% Do your own for practice.

9. Informal Summary
• Program is facts + rules. (horn clauses).
• Query = conjunct of predicates.
• First set of bindings for variables that solve
query are reported. If none, then Prolog
returns no.
• Use “;” to get other solutions.
• Can be viewed as constraint satisfaction
program.

10. MapColoring
• color(r). color(g). color(b).
• colormap(C1,C2,C3):-
color(C1),color(C2),color(C3), C1==C2,
C1==C3, C2==C3.
• Query: colormap(X,Y,Z).
– X = r, Y= g, Z=b.
• Is that it. Yes! Turn on trace.

11. Unification: (matching) terms
• Two terms UNIFY if there is a common
substitution for all variables which makes them
identical.
• f(g(X),Y) = f(Z,Z). % = cheap unification
– X = _G225, Y=g(_G225).
• Look at parse tree for each term.
– variables match
– variable matches anything (set the binding)
– function symbols only match identical function
symbols.

12. Satisfiability: uses unification
• sat(true). % base case
• sat(not(false)). % base case
• sat(or(X,Y)):- sat(X).
• sat(or(X,Y)):-sat(Y).
• sat(and(X,Y)):-sat(X),sat(Y).
• test1(X,Y):- sat(and(not(X),X)).
• test2(X,Y):- sat(and(X,not(Y))).

13. Semantic Network representation
in prolog

14. Semantic Network representation
in prolog
• nodes represent individuals such as the
canary tweety and classes such as ostrich,
crow, robin, bird, and vertebrate.
• isa links represent the class hierarchy
relationship.
• We adopt canonical forms for the data
relationships within the net.

15. Semantic Network
Representation
• We use an isa(Type, Parent) predicate to
indicate that Type is a member of Parent
and a hasprop(Object, Property, Value)
predicate to represent property relations.
• hasprop indicates that Object has Property
with Value. Object and Value are nodes in
the network, and Property is the name of the
link that joins them.

16. isa(canary, bird). hasprop(tweety, color, white)
isa(robin, bird). hasprop(robin, color, red).
isa(ostrich, bird). hasprop(canary, color, yellow).
isa(penguin, bird). hasprop(penguin, color, brown).
isa(bird, animal). hasprop(bird, travel, fly).
isa(fish, animal). hasprop(ostrich, travel, walk).
isa(opus, penguin). hasprop(fish, travel, swim).
isa(tweety, canary). hasprop(robin, sound, sing).
hasprop(canary, sound, sing).
hasprop(bird, cover, feathers). hasprop(animal, cover,
skin).

17. Semantic Network
Representation
• We create a recursive search algorithm to
find whether an object in our semantic net
has a particular property. Properties are
stored in the net at the most general level at
which they are true. Through inheritance, an
individual or subclass acquires the
properties of its superclasses. Thus the
property fly holds for bird and all its
subclasses.

18. Semantic Network
Representation
• hasproperty(Object, Property, Value) :-
hasprop(Object, Property, Value).
hasproperty(Object, Property, Value) :-
isa(Object, Parent), hasproperty(Parent,
Property, Value).

19. Frame Representation
• Semantic nets can be partitioned, with
additional information added to node
descriptions, to give them a frame-like
structure (Minsky 1975, Luger 2009).
• We present the bird example again using
frames, where each frame represents a
collection of relationships of the semantic
net and the isa slots of the frame define the
frame hierarchy as in

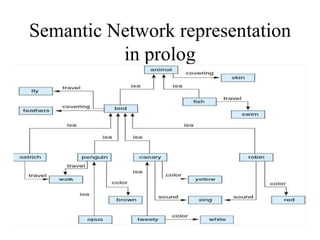
20. Frame Representation
• One way
• frame(name(bird), isa(animal),[travel(flies),
feathers]).
• Other way
• bird(isa,animal).
• bird(fly,wings).

21. Frame Representation
• Which method will be easy for query?

22. DFS
% solve(goal, solution Path)
% s(state, successor-state)
dfs(N,[N]) :- goal(N).
dfs(N,[N|Sol1]):- s(N,N1), dfs(N1,Sol1).
s(a,b). s(a,c). s(b,d). s(b,e). s(c,f).
s(c,g). s(d,h). s(e,i). s(e,j). s(f,k).
goal(i). goal(f).
?- dfs(a,N).
N = [a, b, e, i] ;
N = [a, c, f] ;

23. Limitations
• 2nd order: Can’t ask what is relationship
between heart and lungs?
• Probabilities: What is likelihood of fire
destroying Julian?