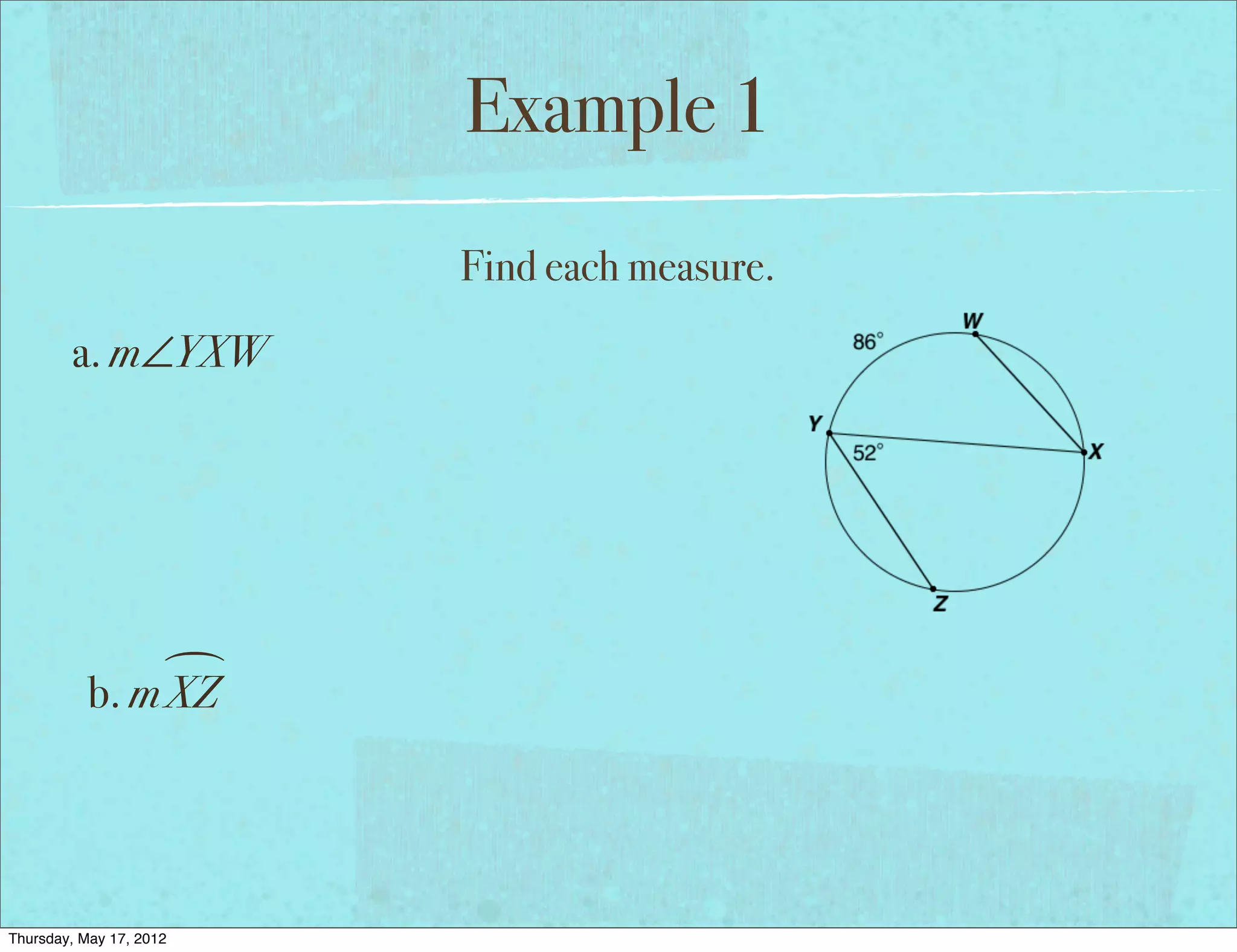
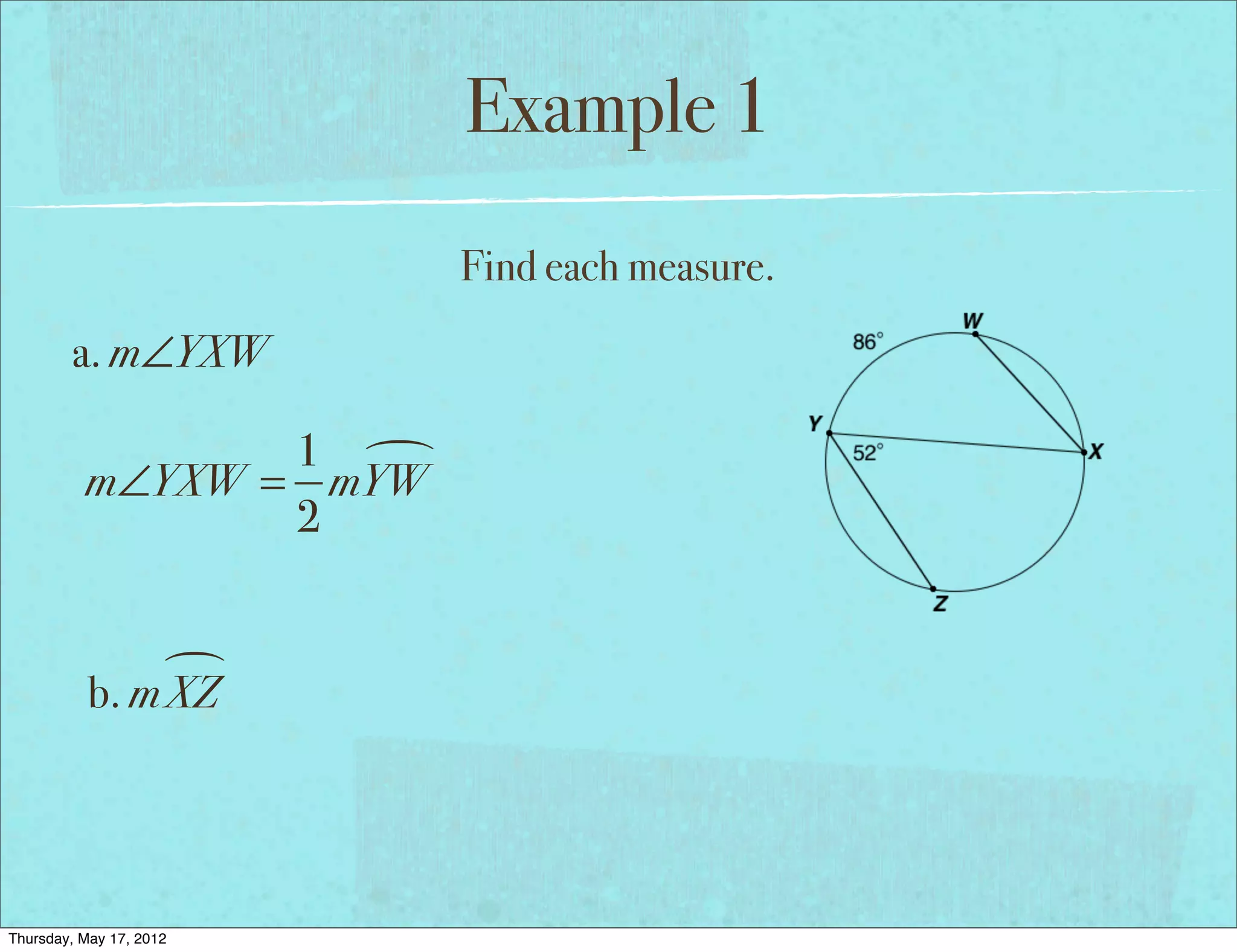
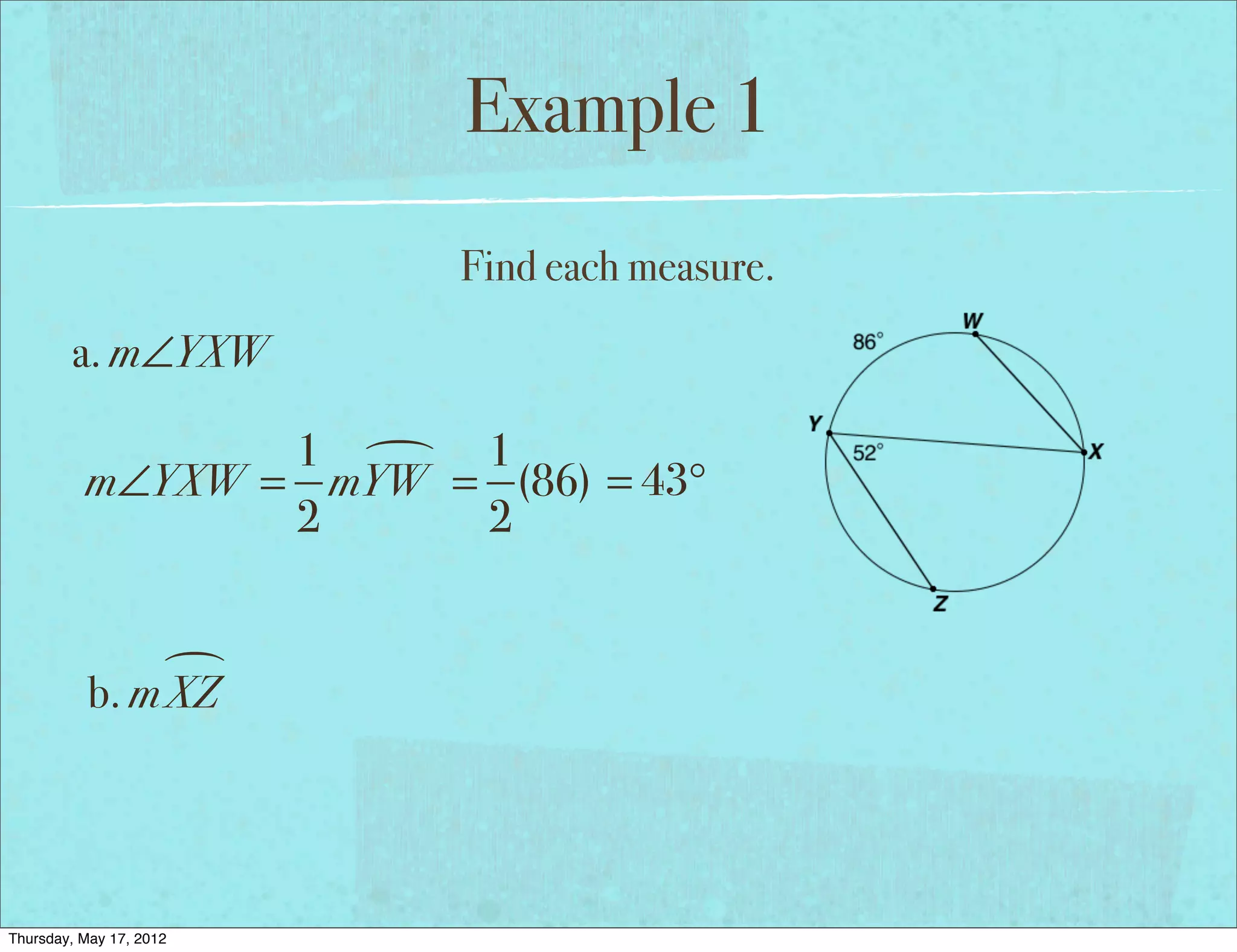
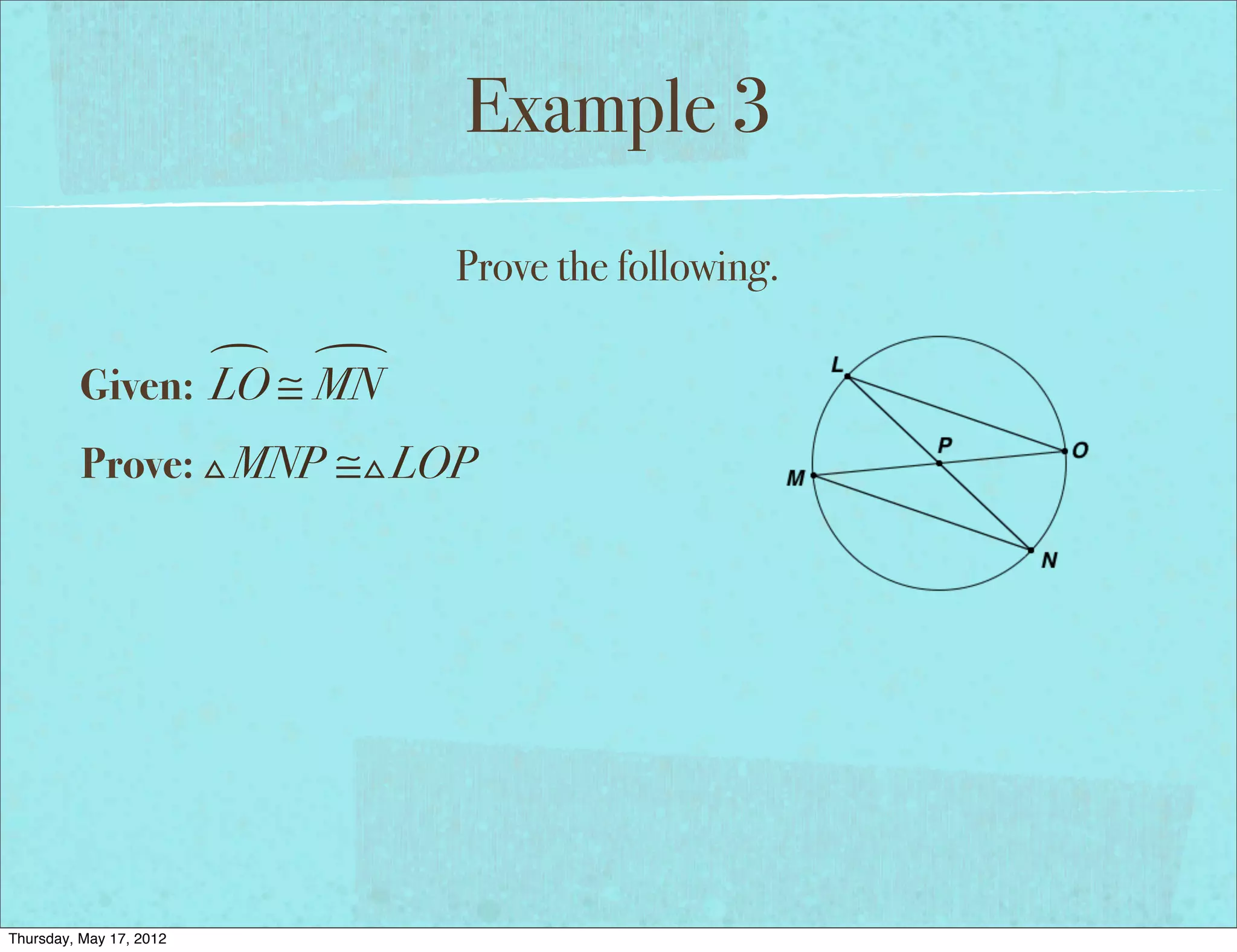
This document provides an overview of inscribed angles including essential questions, vocabulary, theorems, and examples. It defines an inscribed angle as an angle whose vertex is on a circle and whose sides consist of chords of the circle. The inscribed angle theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. Examples demonstrate finding measures of inscribed angles using this theorem as well as solving equations involving inscribed angle measures. The document concludes with a problem set involving additional inscribed angle examples and problems.