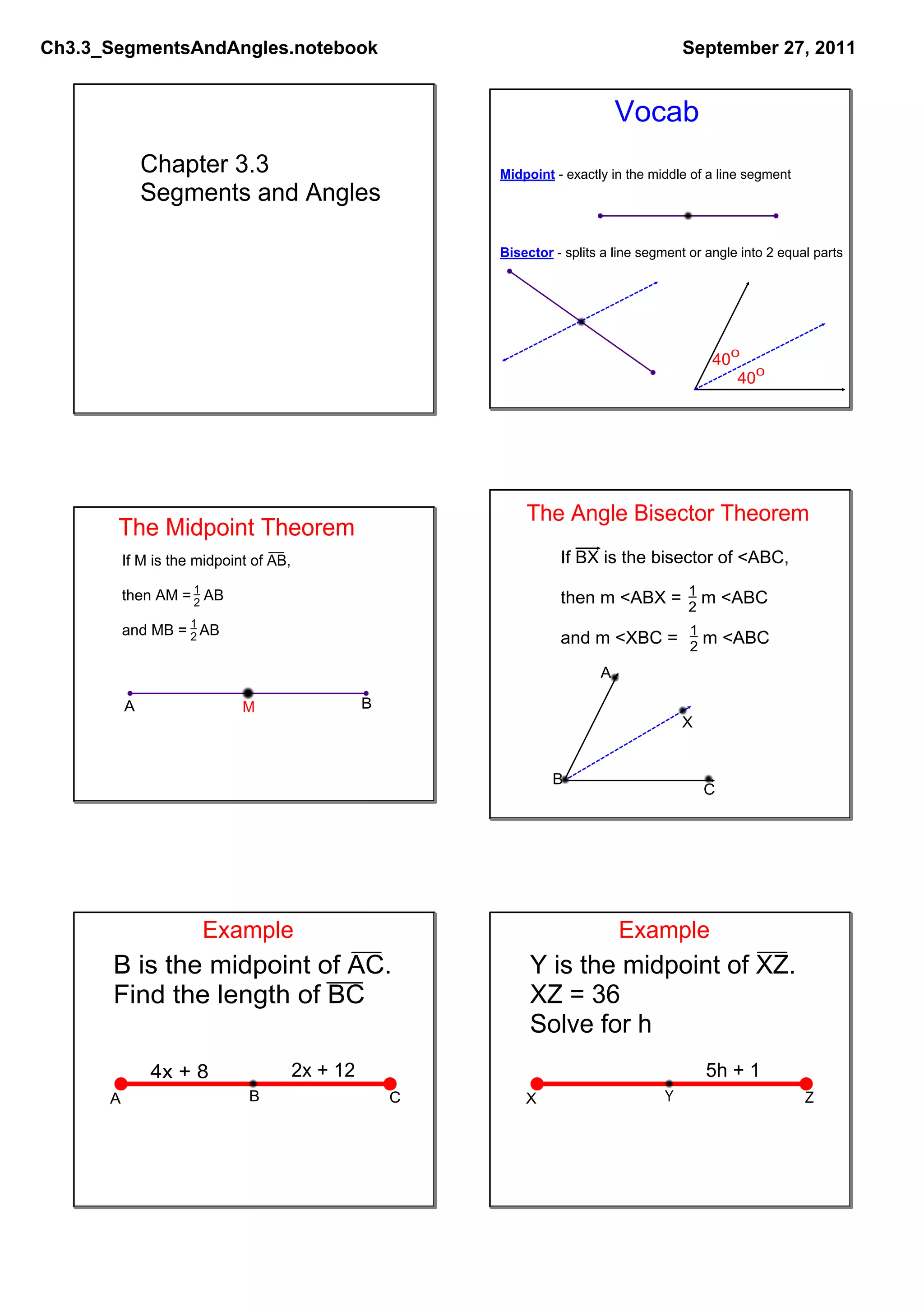
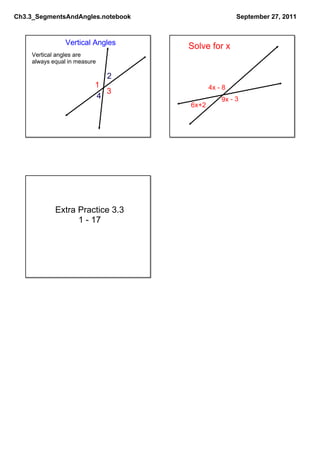
This document discusses segments, angles, and theorems related to them. It introduces the midpoint theorem, which states that if a point M is the midpoint of segment AB, then the distances AM and MB will each be half the length of AB. It also introduces the angle bisector theorem, which states that if BX bisects angle ABC, then the measures of angles ABX and XBC will each be half the measure of ABC. Examples are given to demonstrate applying these theorems. Vertical angles are defined as always being equal in measure. Finally, extra practice problems from 1 to 17 are listed.

1. Ch3.3_SegmentsAndAngles.notebook September 27, 2011
Vocab
Chapter 3.3 Midpoint ­ exactly in the middle of a line segment
Segments and Angles
Bisector ­ splits a line segment or angle into 2 equal parts
400
400
The Angle Bisector Theorem
The Midpoint Theorem
If M is the midpoint of AB, If BX is the bisector of <ABC,
1 1
then AM = AB
2 then m <ABX = m <ABC
2
1
and MB = AB 1
2 and m <XBC = m <ABC
2
A
A M B
X
B
C
Example Example
B is the midpoint of AC. Y is the midpoint of XZ.
Find the length of BC XZ = 36
Solve for h
4x + 8 2x + 12 5h + 1
A B C X Y Z

2. Ch3.3_SegmentsAndAngles.notebook September 27, 2011
Vertical Angles
Solve for x
Vertical angles are
always equal in measure
2
1 4x ­ 8
3
4 9x ­ 3
6x+2
Extra Practice 3.3
1 ­ 17