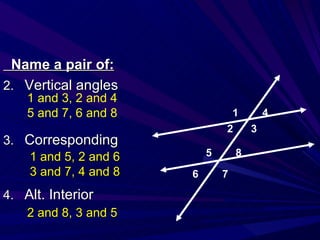
This document contains a daily homework quiz on triangles, followed by review questions testing knowledge of geometry vocabulary and properties of angles, lines, polygons. It concludes with exercises identifying pairs of angles and finding missing angle measures in diagrams.

1. Daily Homework Quiz For use after Lesson 8.2 1. What is an acute triangle? 2. Can a right triangle be isosceles?

2. Daily Homework Quiz For use after Lesson 8.2 1. What is an acute triangle? 2. Can a right triangle be isosceles? ANSWER a triangle with three acute angles ANSWER yes

3. 8.1 – 8.4 Review

4. Essential Questions Why is it important to be able to identify congruent triangles in everyday life? Where in real life can you use the properties of isosceles and equilateral triangles? How are the relationships between lines and planes used in the real world? What areas in the real world are properties of parallel lines important?

5. Vocabulary Review A quick check on vocabulary from this unit.

6. An angle that measures between 1 & 90 ° The angles whose sum is 180 ° An angle that measures exactly 180 ° A triangle with exactly one 90 ° angle A flat surface that extends infinitely An angle that measures between 90 &180 ° Has one endpoint and extends infinitely in one direction

7. An angle that measures between 1 & 90 ° The angles whose sum is 180 ° An angle that measures exactly 180 ° A triangle with exactly one 90 ° angle A flat surface that extends infinitely An angle that measures between 90 &180 ° Has one endpoint and extends infinitely in one direction supplementary straight right plane obtuse ray

8. 8. A five-sided polygon 9. A 10-sided polygon 10. A triangle with 3  sides 11. A quadrilateral with 2 pairs of parallel sides 12. A triangle with no  sides 13. A quadrilateral with exactly one pair of parallel sides

9. 8. A five-sided polygon 9. A 10-sided polygon 10. A triangle with 3  sides 11. A quadrilateral with 2 pairs of parallel sides 12. A triangle with no  sides 13. A quadrilateral with exactly one pair of parallel sides pentagon decagon equilateral parallelogram scalene trapezoid

10. 14. A parallelogram with 4  sides 15. A quadrilateral with 4  90 degrees angles 16. Connects two vertices of a polygon that do not share a side 17. A six-sided figure 18. A seven-sided figure

11. 14. A parallelogram with 4  sides 15. A quadrilateral with 4  90 degrees angles 16. Connects two vertices of a polygon that do not share a side 17. A six-sided figure 18. A seven-sided figure rhombus Rectangle diagonal hexagon heptagon

12. 19. Two angles whose sum is 90 ° 20. Has two endpoints, can be measured, and is a part of a line 21. Angles formed when two lines intersect and are always congruent

13. 19. Two angles whose sum is 90 ° 20. Has two endpoints, can be measured, and is a part of a line 21. Angles formed when two lines intersect and are always congruent complementary Line segment vertical

14. 22. A line that crosses two or more lines 23. Lines (on same plane) that never intersect 24. Lines that meet at 90° angles 25. The point where two rays meet and form an angle 26. A many-sided figure

15. 22. A line that crosses two or more lines 23. Lines (on same plane) that never intersect 24. Lines that meet at 90° angles 25. The point where two rays meet and form an angle 26. A many-sided figure transversal parallel perpendicular vertex polygon

16. 27. A polygon with 8 sides 28. A polygon with all congruent sides and all congruent angles 29. A polygon that does not have all congruent sides or angles

17. 27. A polygon with 8 sides 28. A polygon with all congruent sides and all congruent angles 29. A polygon that does not have all congruent sides or angles octagon Regular polygon Irregular polygon

18. Name a pair of: Vertical angles Corresponding Alt. Interior 1 4 2 3 5 8 6 7

19. Name a pair of: Vertical angles Corresponding Alt. Interior 1 and 3, 2 and 4 5 and 7, 6 and 8 1 and 5, 2 and 6 3 and 7, 4 and 8 2 and 8, 3 and 5 1 4 2 3 5 8 6 7

20. Name a pair of: Alt. Exterior Supplementary 1 4 2 3 5 8 6 7

21. Name a pair of: Alt. Exterior Supplementary 1 and 7, 4 and 6 1 and 4, 4 and 3, 3 and 2, 1 and 2, 5 and 8, 8 and 7, 7 and 6, 6 and 5 1 4 2 3 5 8 6 7

22. Find all angle measures 1 3 t 113  2 5 6 7 8 113  113  113 

23. Find all angle measures 1 67  3 t 113  180 - 67 2 5 6 7 8 67  67  67  113  113  113 

24. Homework Page 808 #1-11 Test tomorrow! All late work due tomorrow!