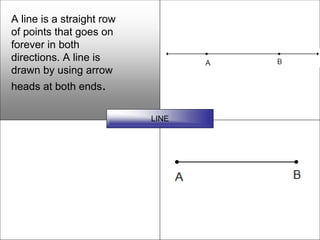
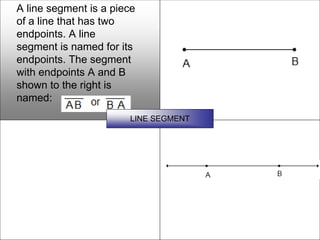
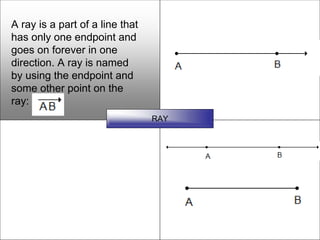
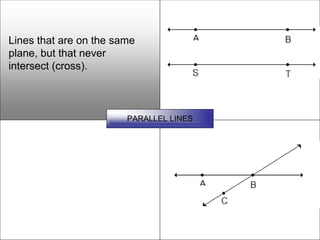
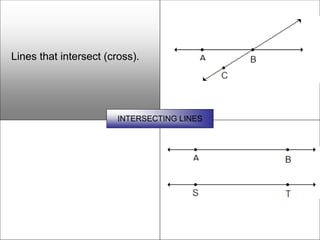
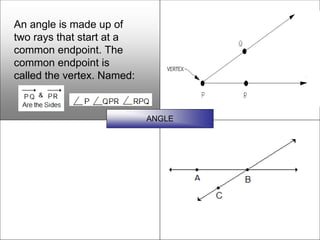
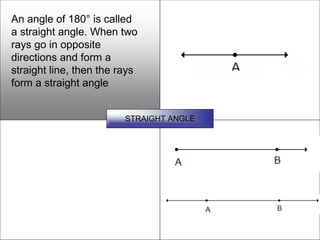
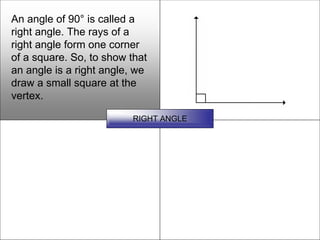
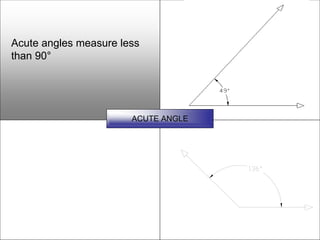
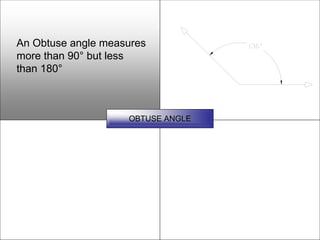
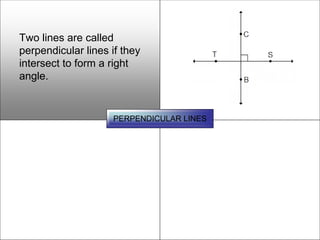
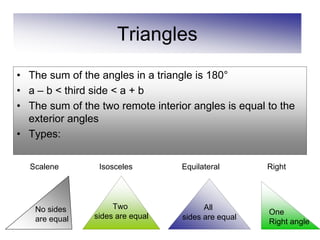
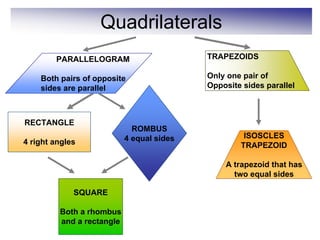
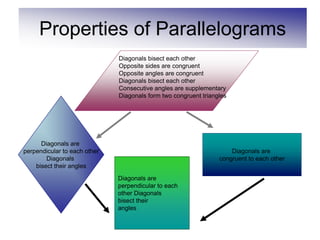
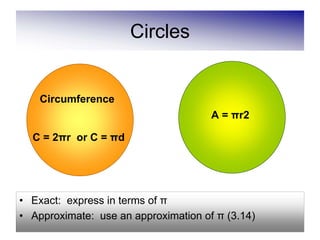
This document defines and describes various geometric shapes and concepts. It defines points, lines, line segments, rays, angles, parallel lines, triangles, quadrilaterals such as parallelograms, rectangles, squares, trapezoids, and rhombi. It also covers circles, areas, volumes, and properties of angles, triangles, parallelograms and polygons. Key concepts include classifying angles as acute, obtuse, right or straight, and properties of parallel lines, perpendicular lines, complementary and supplementary angles.

1. Geometry
Concepts
Point
Line Ray
Line segment
Ray
Angles
Parallel Lines
Triangles
Quadrilaterals
Parallelograms
Area
Circles
Volume

2. A point can be described
as a location in space.
Represented by a dot and
is named by writing a
capital letter next to the
dot.
POINT

3. A line is a straight row
of points that goes on
forever in both
directions. A line is
drawn by using arrow
heads at both ends.
LINE

4. A line segment is a piece
of a line that has two
endpoints. A line
segment is named for its
endpoints. The segment
with endpoints A and B
shown to the right is
named:
LINE SEGMENT

5. A ray is a part of a line that
has only one endpoint and
goes on forever in one
direction. A ray is named
by using the endpoint and
some other point on the
ray:
RAY

6. Lines that are on the same
plane, but that never
intersect (cross).
PARALLEL LINES

7. Lines that intersect (cross).
INTERSECTING LINES

8. Types of Angles
• Classification
– Acute angle: all angles are less than 90°
– Obtuse angle: one angle is greater than 90°
– Right angle: has one angle equal to 90°
• Complementary angle: the sum of two angles is 90°
• Supplementary angle: the sum of two angles is 180°
• Adjacent angle: angles that share a side

9. An angle is made up of
two rays that start at a
common endpoint. The
common endpoint is
called the vertex. Named:
ANGLE

10. Angles can be measured in
degrees. The symbol for
degrees is a small raised
circle °
DEGREES

11. An angle of 180° is called
a straight angle. When two
rays go in opposite
directions and form a
straight line, then the rays
form a straight angle
STRAIGHT ANGLE

12. An angle of 90° is called a
right angle. The rays of a
right angle form one corner
of a square. So, to show that
an angle is a right angle, we
draw a small square at the
vertex.
RIGHT ANGLE

13. Acute angles measure less
than 90°
ACUTE ANGLE

14. An Obtuse angle measures
more than 90° but less
than 180°
OBTUSE ANGLE

15. Two lines are called
perpendicular lines if they
intersect to form a right
angle.
PERPENDICULAR LINES

16. Two angles are called
complementary angles if
the sum of their measures
is 90°. If two angles are
complementary , each
angle is the complement
of the other.
COMPLEMENTARY ANGLES

17. Two angles are called
supplementary angles if the
sum of their measures is
180°
SUPPLEMENTARY ANGLES

18. Triangles
• The sum of the angles in a triangle is 180°
• a – b < third side < a + b
• The sum of the two remote interior angles is equal to the
exterior angles
• Types:
Scalene Isosceles Equilateral Right
No sides Two All
One
are equal sides are equal sides are equal
Right angle

19. Polygons
• The sum of the interior angles: (n - 2)(180°)
• Classified by number of sides (n)
– Triangle (3)
– Quadrilateral (4)
– Pentagon (5)
– Hexagon (6)
– Heptagon (7)
– Octagon (8)
– Nonagon (9)
– Decagon (10)
• Regular Polygon: all sides are congruent

20. Quadrilaterals
PARALLELOGRAM TRAPEZOIDS
Both pairs of opposite Only one pair of
sides are parallel Opposite sides parallel
RECTANGLE
ROMBUS
4 equal sides ISOSCLES
4 right angles TRAPEZOID
A trapezoid that has
two equal sides
SQUARE
Both a rhombus
and a rectangle

21. Properties of Parallelograms
Diagonals bisect each other
Opposite sides are congruent
Opposite angles are congruent
Diagonals bisect each other
Consecutive angles are supplementary
Diagonals form two congruent triangles
Diagonals are
perpendicular to each other Diagonals are
Diagonals congruent to each other
bisect their angles
Diagonals are
perpendicular to each
other Diagonals
bisect their
angles

22. Circles
Circumference
A = πr2
C = 2πr or C = πd
• Exact: express in terms of π
• Approximate: use an approximation of π (3.14)