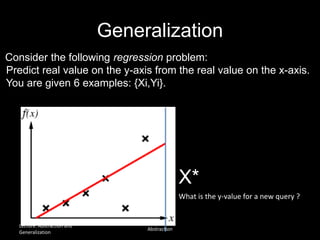
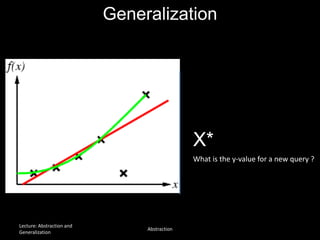
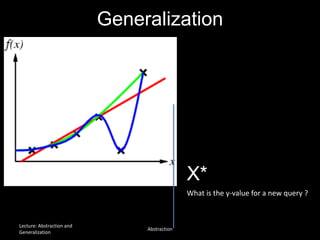
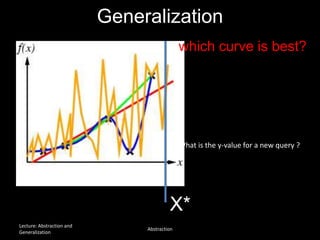
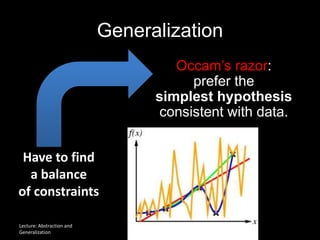
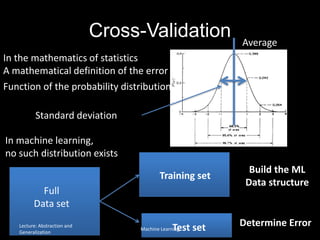
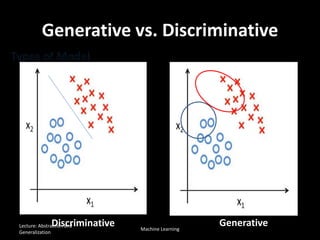
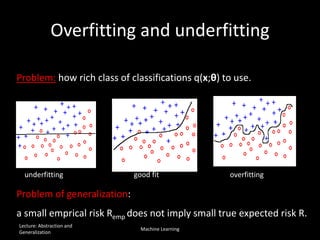
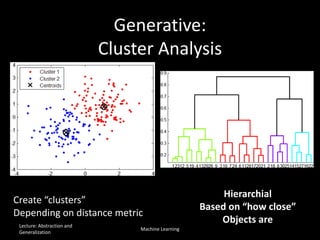
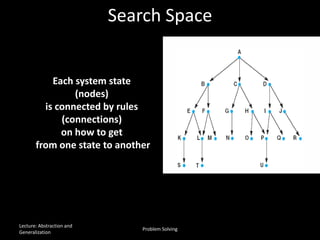
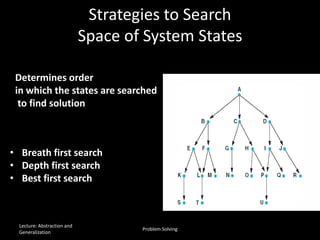
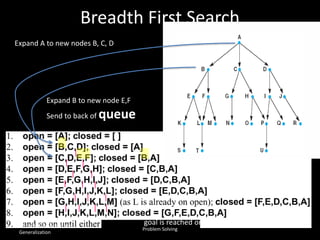
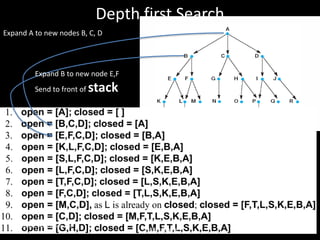
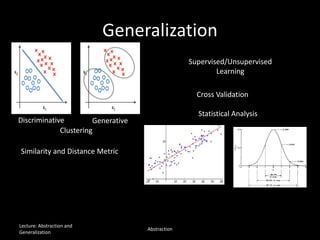
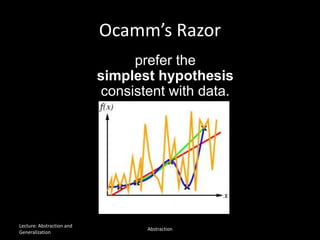
The document discusses the concepts of abstraction and generalization in knowledge representation and problem-solving, emphasizing the importance of choosing the right representation of reality based on specific aspects to be modeled. It explores various machine learning techniques, including supervised and unsupervised learning, pattern recognition, and classification algorithms, touching on statistical methods and the challenges of overfitting and underfitting. Additionally, it outlines problem-solving strategies within search spaces, including breadth-first, depth-first, and best-first search methods, and highlights the significance of heuristics in optimizing search algorithms.

1. Use of Knowledge
Abstraction and Problem Solving
Abstraction and Problem Solving
Edward (Ned) Blurock
Lecture: Abstraction and
Generalization
Abstraction

2. Knowledge Representation
Abstraction
You choose how to represent reality
The choice is not unique
It depends on what aspect of reality you want to represent and how
Lecture: Abstraction and
Generalization
Abstraction

3. Concept Abstraction
Organizing and making sense of the immense amount of
data/knowledge we have
Generalization
The ability of an algorithm to perform accurately on new, unseen
examples after having trained on a learning data set
Lecture: Abstraction and
Generalization
Abstraction

4. Generalization
Consider the following regression problem:
Predict real value on the y-axis from the real value on the x-axis.
You are given 6 examples: {Xi,Yi}.
X*
What is the y-value for a new query ?
Lecture: Abstraction and
Generalization
Abstraction

5. Generalization
X*
What is the y-value for a new query ?
Lecture: Abstraction and
Generalization
Abstraction

6. Generalization
X*
What is the y-value for a new query ?
Lecture: Abstraction and
Generalization
Abstraction

7. Generalization
which curve is best?
X*
What is the y-value for a new query ?
Lecture: Abstraction and
Generalization
Abstraction

8. Generalization
Occam’s razor:
prefer the
simplest hypothesis
consistent with data.
Have to find
a balance
of constraints
Lecture: Abstraction and
Generalization
Abstraction

9. Two Schools of Thought
1. Statistical “Learning”
The data is reduced to vectors of numbers
Statistical techniques are used for the tasks to be performed.
Formulate a hypothesis and prove it is true/false
2. Structural “Learning”
The data is converted to a discrete structure
(such as a grammar or a graph) and the
techniques are related to computer science
subjects (such as parsing and graph matching).
Lecture: Abstraction and
Generalization
Machine Learning

10. A spectrum of machine learning tasks
• High-dimensional data (e.g. more
than 100 dimensions)
• The noise is not sufficient to
obscure the structure in the data
if we process it right.
• There is a huge amount of
structure in the data, but the
structure is too complicated to be
represented by a simple model.
• The main problem is figuring out
a way to represent the
complicated structure that allows
it to be learned.
• Low-dimensional data (e.g. less
than 100 dimensions)
• Lots of noise in the data
• There is not much structure in the
data, and what structure there is,
can be represented by a fairly
simple model.
• The main problem is
distinguishing true structure from
noise.
Statistics Artificial Intelligence
Lecture: Abstraction and
Generalization
Machine Learning

11. Supervised
learning
Un-Supervised
learning
Concept Acquisition
Statistics
Lecture: Abstraction and
Generalization
Machine Learning

12. learning with the presence of an expert
Data is labelled with a class or value
Goal:: predict class or value label
c1
c2
c3
Supervised Learning
Learn a properties of a classification
Decision making
Predict (classify) sample → discrete set of class labels
e.g. C = {object 1, object 2 … } for recognition task
e.g. C = {object, !object} for detection task
Spa
m
No-
Spam
Lecture: Abstraction and
Generalization
Machine Learning

13. learning without the presence of an expert
Data is unlabelled with a class or value
Goal::
determine data patterns/groupings
and the properties of that classification
Unsupervised Learning
Association or clustering::
grouping a set of instances by attribute similarity
e.g. image segmentation
Key concept: Similarity
Lecture: Abstraction and
Generalization
Machine Learning

14. Statistical Methods
Regression::
Predict sample → associated real (continuous) value
e.g. data fitting
x1
x2
Learning within the constraints of the method
Data is basically n-dimensional set of numerical attributes
Deterministic/Mathematical algorithms based on
probability distributions
Principle Component Analysis::
Transform to a new (simpler) set of coordinates
e.g. find the major component of the data
What is the probability that this hypothesis is true?
Lecture: Abstraction and
Generalization
Machine Learning

15. Pattern Recognition
Another name for machine learning
• A pattern is an object, process or event that can be given a
name.
• A pattern class (or category) is a set of patterns sharing
common attributes and usually originating from the same
source.
• During recognition (or classification) given objects are
assigned to prescribed classes.
• A classifier is a machine which performs classification.
“The assignment of a physical object or event to one of several prespecified
categeries” -- Duda & Hart
Lecture: Abstraction and
Generalization
Machine Learning

16. Cross-Validation
In the mathematics of statistics
A mathematical definition of the error
Function of the probability distribution
Average
Standard deviation
In machine learning,
no such distribution exists
Full
Data set
Training set
Test set
Build the ML
Data structure
Determine ErrorLecture: Abstraction and
Generalization
Machine Learning

17. Classification algorithms
– Fisher linear discriminant
– KNN
– Decision tree
– Neural networks
– SVM
– Naïve bayes
– Adaboost
– Many many more ….
– Each one has its properties with respect to:
bias, speed, accuracy, transparency…Lecture: Abstraction and
Generalization
Machine Learning

18. Feature extraction
Task: to extract features which are good for classification.
Good features:
• Objects from the same class have similar feature values.
• Objects from different classes have different values.
“Good” features “Bad” featuresLecture: Abstraction and
Generalization
Machine Learning

19. Similarity
Two objects
belong to the
same classification
If
The are “close”
x1
x2
?
?
?
?
?
Distance between them is small
Need a function
F(object1, object1) = “distance” between them
Lecture: Abstraction and
Generalization
Machine Learning

20. Similarity measure
Distance metric
• How do we measure what it means to be “close”?
• Depending on the problem we should choose an appropriate
distance metric.
For example: Least squares distance in a vector of values
f (a,b) = (ai -bi )2
i=1
n
å
Lecture: Abstraction and
Generalization
Machine Learning

21. Types of Model
Discriminative Generative
Generative vs. Discriminative
Lecture: Abstraction and
Generalization
Machine Learning

22. Overfitting and underfitting
Problem: how rich class of classifications q(x;θ) to use.
underfitting overfittinggood fit
Problem of generalization:
a small emprical risk Remp does not imply small true expected risk R.
Lecture: Abstraction and
Generalization
Machine Learning

23. Generative:
Cluster Analysis
Create “clusters”
Depending on distance metric
Hierarchial
Based on “how close”
Objects areLecture: Abstraction and
Generalization
Machine Learning

24. KNN – K nearest neighbors
x1
x2
?
?
?
?
– Find the k nearest neighbors of the test example , and infer
its class using their known class.
– E.g. K=3
– 3 clusters/groups
?
Lecture: Abstraction and
Generalization
Machine Learning

25. Discrimitive:
Support Vector Machine
• Q: How to draw the optimal linear
separating hyperplane?
 A: Maximizing margin
• Margin maximization
– The distance between H+1 and H-1:
– Thus, ||w|| should be minimizedMargin
Lecture: Abstraction and
Generalization
Machine Learning

26. PROBLEM SOLVING
Algorithms and Complexity
Lecture: Abstraction and
Generalization
Problem Solving

27. Using Knowledge
Problem Solving
Simulations
Searching for a solution
Combining models
to form a large comprehensive model
Lecture: Abstraction and
Generalization
Problem Solving

28. Problem Solving
Basis of the search
Order in which nodes are evaluated and expanded
Determined by Two Lists
OPEN: List of unexpanded nodes
CLOSED: List of expanded nodes
Searching for a solution through all possible solutions
Fundamental algorithm in artificial intelligence
Graph Search
Lecture: Abstraction and
Generalization
Problem Solving

29. Abstraction:
State of a system
chess
Tic-tak-toe
Water jug problem
Traveling salemen’s problem
In problem solving:
Search for the
steps
leading to the solution
The individual steps
are the
states of the system
Lecture: Abstraction and
Generalization
Problem Solving

30. Solution Space
The set of all states of the problem
Including the goal state(s)
All possible board combinations
All possible reference points
All possible combinations
State of the system:
An object in the search space
Lecture: Abstraction and
Generalization
Problem Solving

31. Search Space
Each system state
(nodes)
is connected by rules
(connections)
on how to get
from one state to another
Lecture: Abstraction and
Generalization
Problem Solving

32. Search Space
How the states are connected
Legal moves
Paths between points Possible operations
Lecture: Abstraction and
Generalization
Problem Solving

33. Strategies to Search
Space of System States
• Breath first search
• Depth first search
• Best first search
Determines order
in which the states are searched
to find solution
Lecture: Abstraction and
Generalization
Problem Solving

34. Breadth-first searching
• A breadth-first search (BFS)
explores nodes nearest the
root before exploring nodes
further away
• For example, after searching
A, then B, then C, the search
proceeds with D, E, F, G
• Node are explored in the
order A B C D E F G H I J K L
M N O P Q
• J will be found before NL M N O P
G
Q
H JI K
FED
B C
A
Lecture: Abstraction and
Generalization
Problem Solving

35. Depth-first searching
• A depth-first search (DFS)
explores a path all the way to
a leaf before backtracking and
exploring another path
• For example, after searching
A, then B, then D, the search
backtracks and tries another
path from B
• Node are explored in the
order A B D E H L M N I
O P C F G J K Q
• N will be found before JL M N O P
G
Q
H JI K
FED
B C
A
Lecture: Abstraction and
Generalization
Problem Solving

36. Breadth First Search
|
| |
||
| | |
| | |
||||
Items between red bars are siblings.
goal is reached or open is empty.
Expand A to new nodes B, C, D
Expand B to new node E,F
Send to back of queue
Queue: FILO
Lecture: Abstraction and
Generalization
Problem Solving

37. Depth first Search
Expand A to new nodes B, C, D
Expand B to new node E,F
Send to front of stack
Stack: FIFO
Lecture: Abstraction and
Generalization
Problem Solving

38. Best First Search
Breadth first search: queue (FILO)
Depth first search: stack (FIFO)
Uninformed searches:
No knowledge of how good the current solution is
(are we on the right track?)
Best First Search: Priority Queue
Associated with each node is a heuristic
F(node) = the quality of the node to lead to a final solution
Lecture: Abstraction and
Generalization
Problem Solving

39. A* search
• Idea: avoid expanding paths that are already expensive
•
• Evaluation function f(n) = g(n) + h(n)
•
• g(n) = cost so far to reach n
• h(n) = estimated cost from n to goal
• f(n) = estimated total cost of path through n to goal
This is the hard/unknown part
If h(n) is an underestimate, then the algorithm is guarenteed to find a solution
Lecture: Abstraction and
Generalization
Problem Solving

40. Admissible heuristics
• A heuristic h(n) is admissible if for every node n,
h(n) ≤ h*(n), where h*(n) is the true cost to reach
the goal state from n.
• An admissible heuristic never overestimates the cost
to reach the goal, i.e., it is optimistic
• Example: hSLD(n) (never overestimates the actual
road distance)
• Theorem: If h(n) is admissible, A* using TREE-
SEARCH is optimal
Lecture: Abstraction and
Generalization
Problem Solving

41. Graph Search
Several Structures Used
Graph Search
The graph as search space
Breadth first search Queue
Depth first search Stack
Best first search Priority Queue
Stacks and queues, depending on search strategy
Lecture: Abstraction and
Generalization
Problem Solving

42. Abstraction and Representation
Lecture: Abstraction and
Generalization
Abstraction
Abstraction
The process of determining
key concepts to
represent
reality

43. Sources of Abstraction
Lecture: Abstraction and
Generalization
Abstraction
The Modeler Abstracted from Data
Design Decisions (Semi-) Automated

44. Generalization
Lecture: Abstraction and
Generalization
Abstraction
Statistical Analysis
Clustering
Discriminative Generative
Supervised/Unsupervised
Learning
Cross Validation
Similarity and Distance Metric

45. Ocamm’s Razor
Lecture: Abstraction and
Generalization
Abstraction
prefer the
simplest hypothesis
consistent with data.

46. Using Knowledge
Lecture: Abstraction and
Generalization
Abstraction
• Breath first search
• Depth first search
• Best first search
Searching for solutions
Search Space State of system