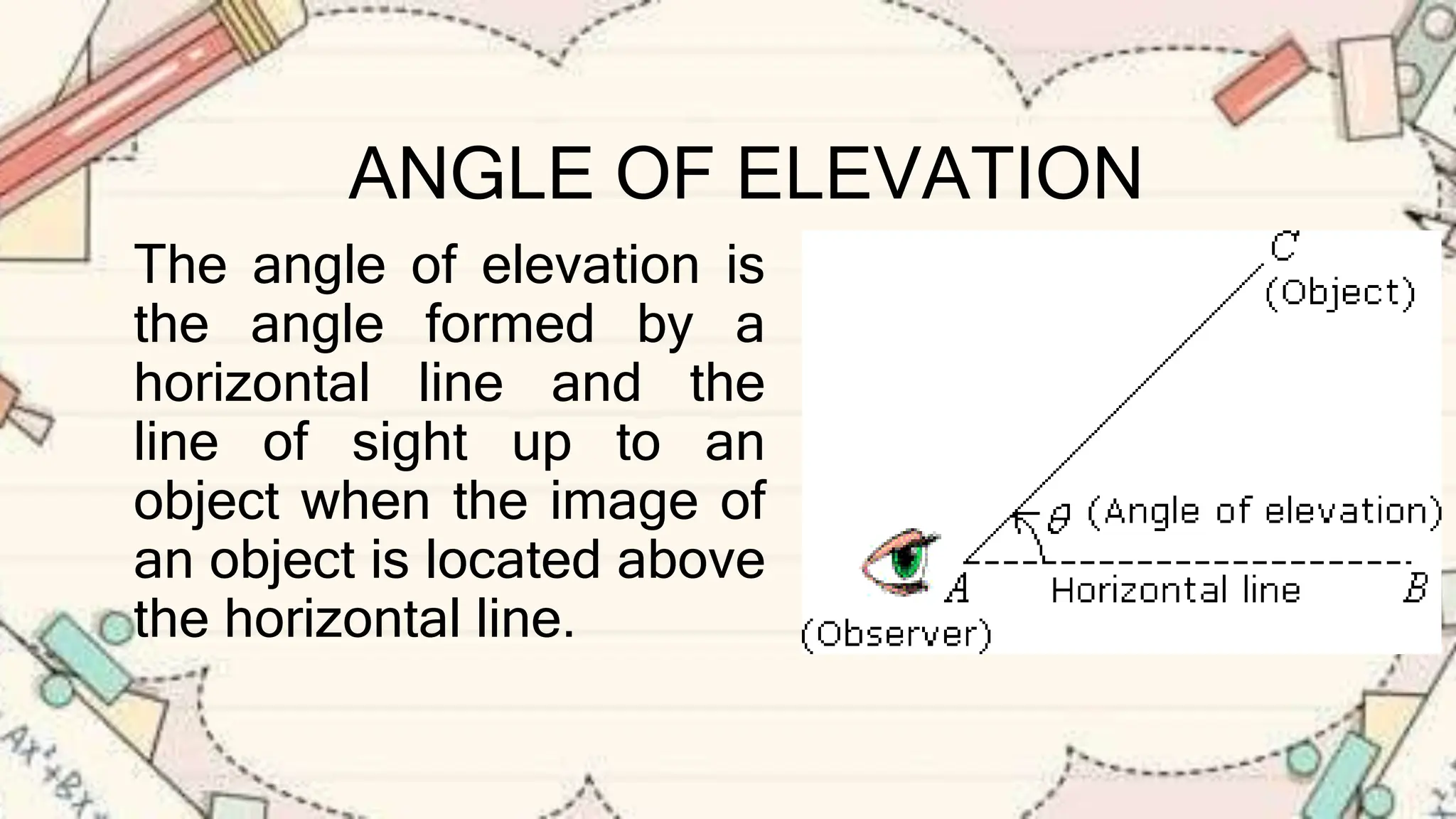
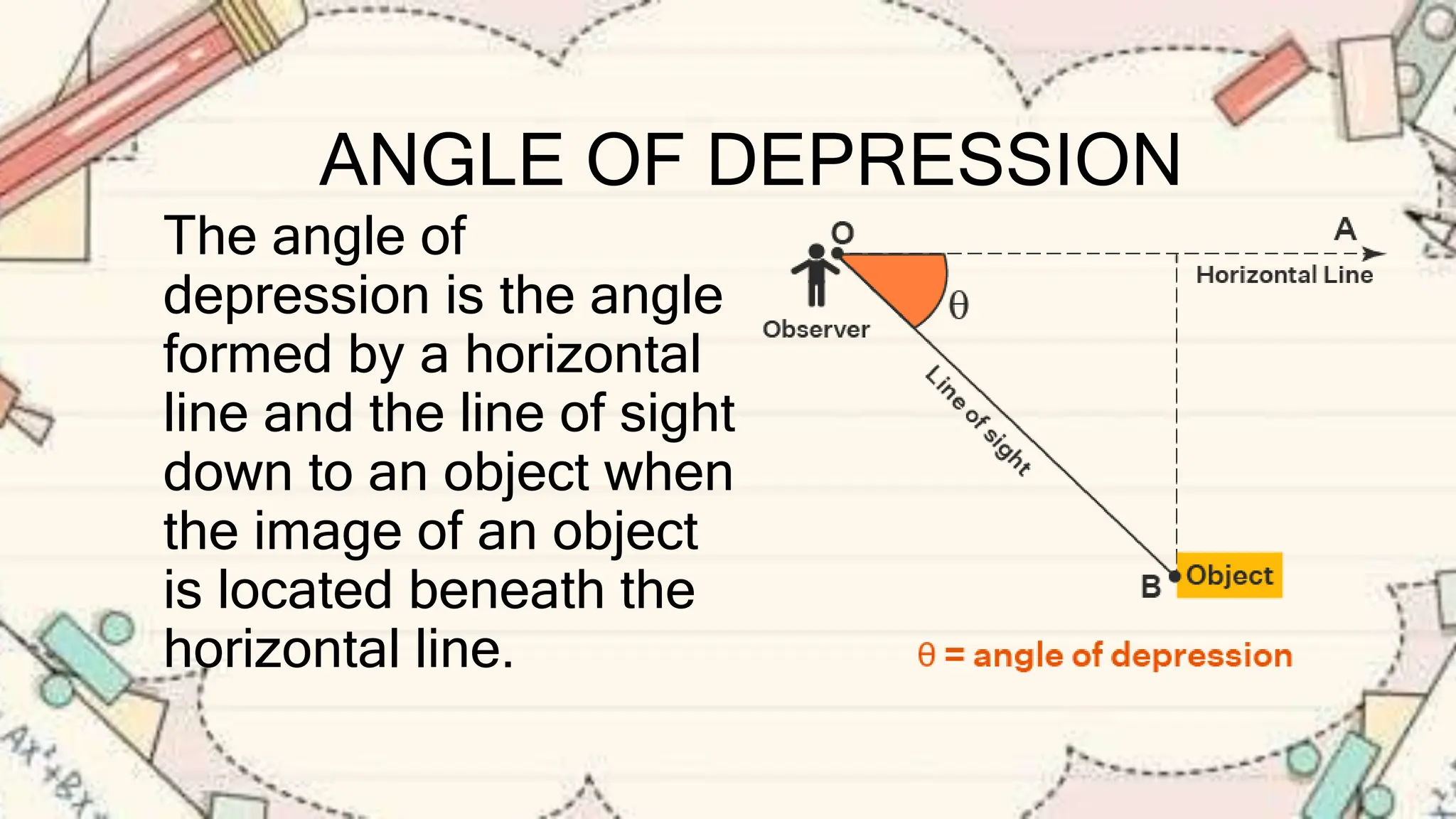
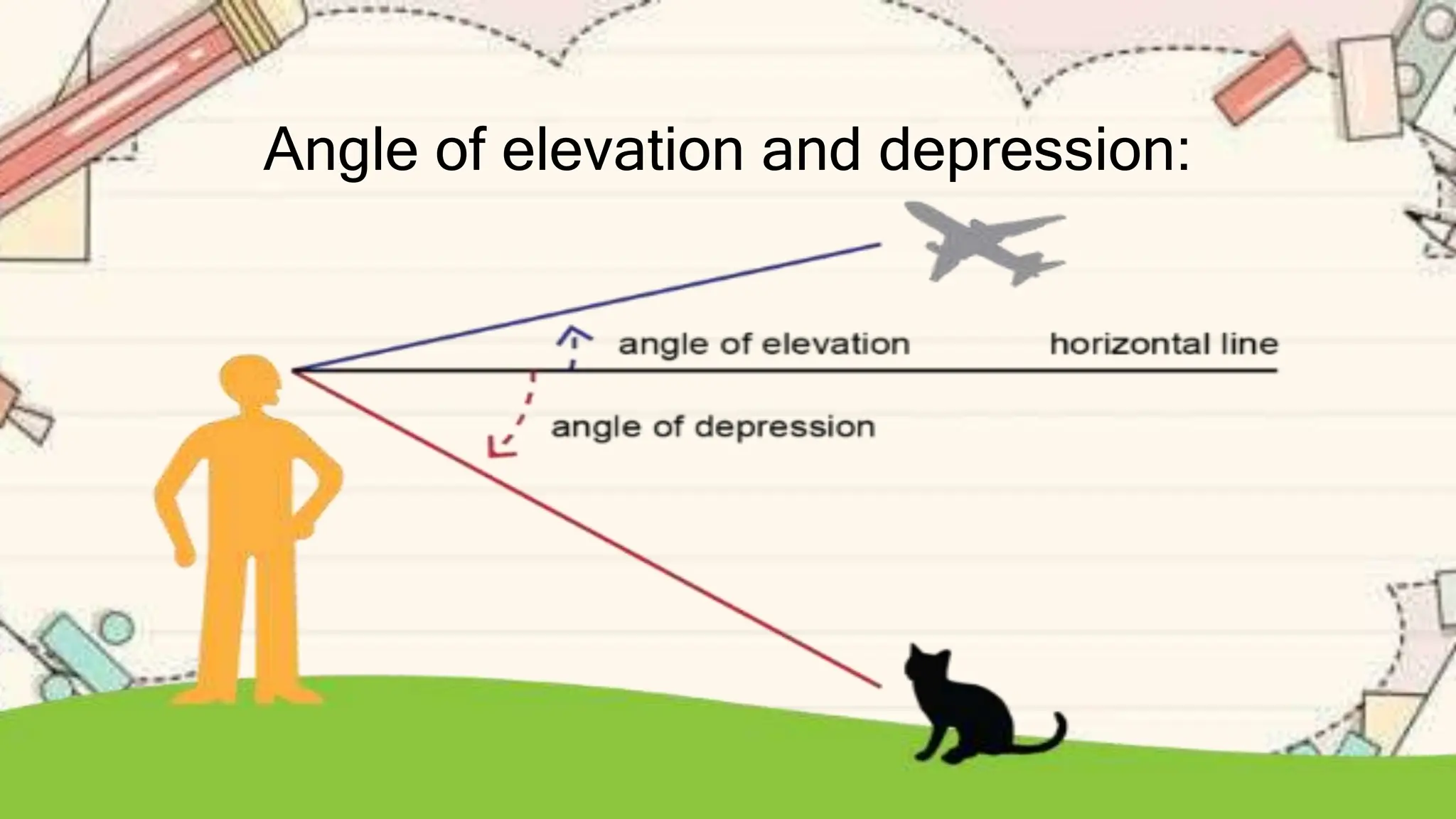
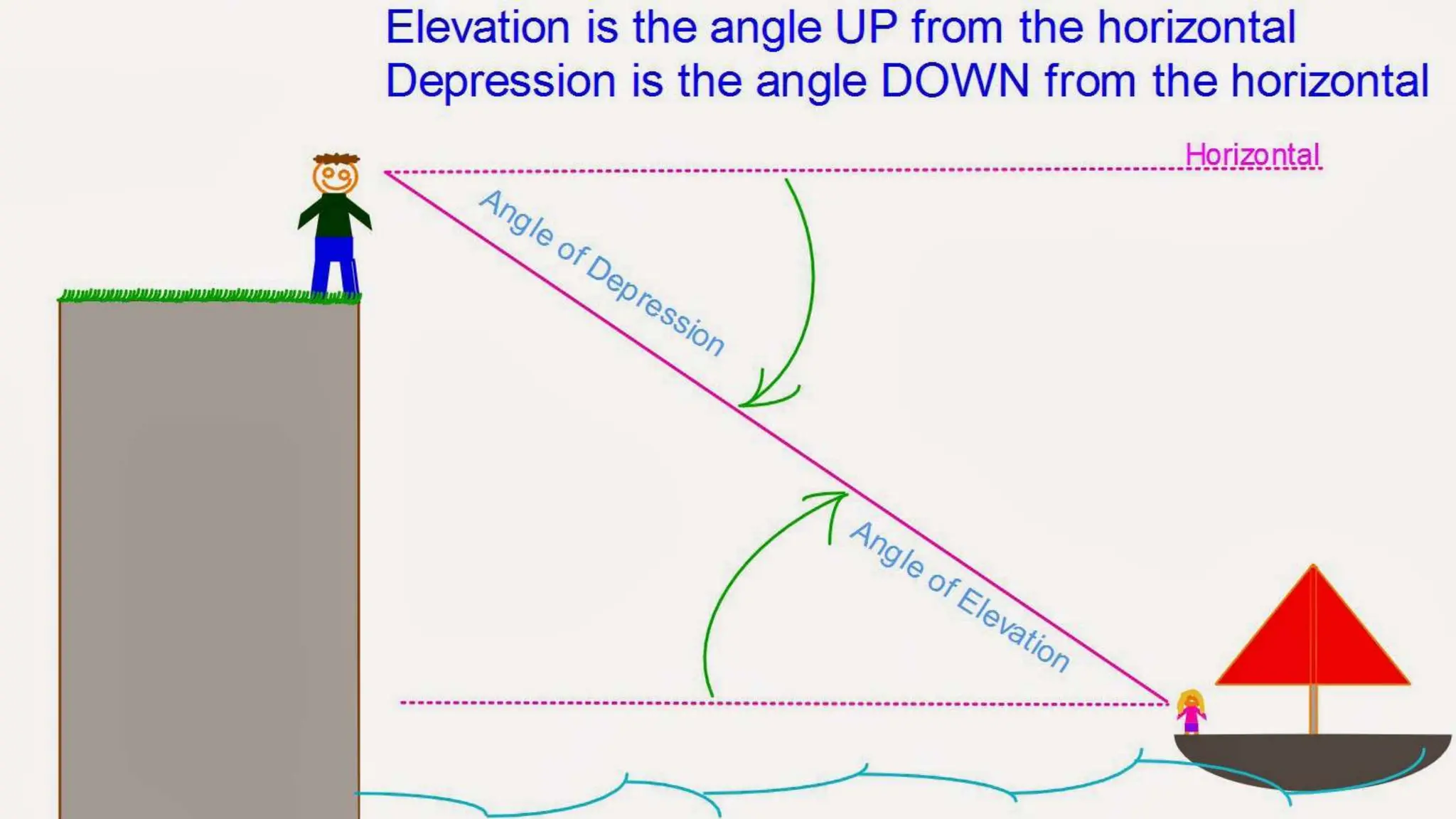
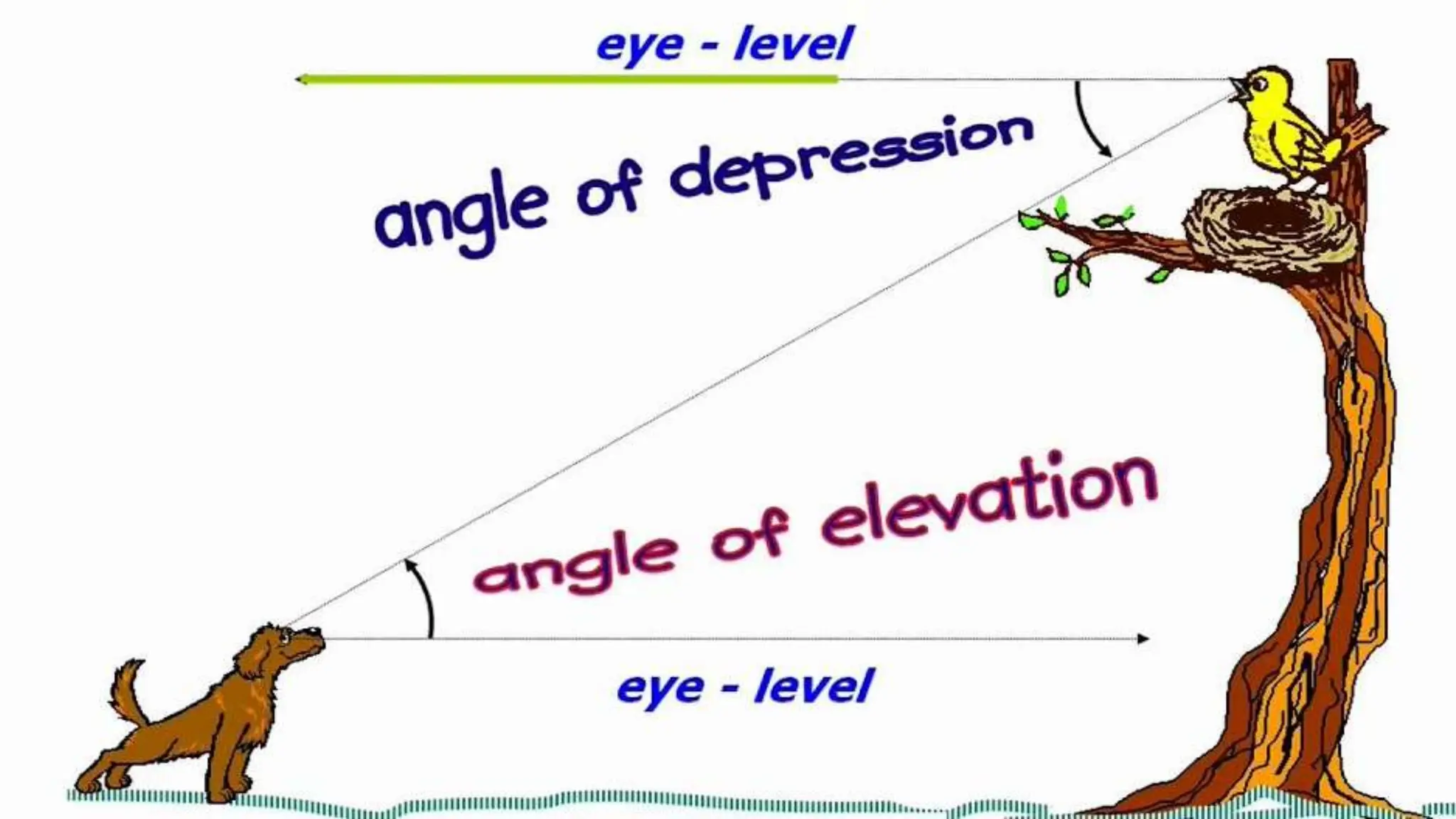
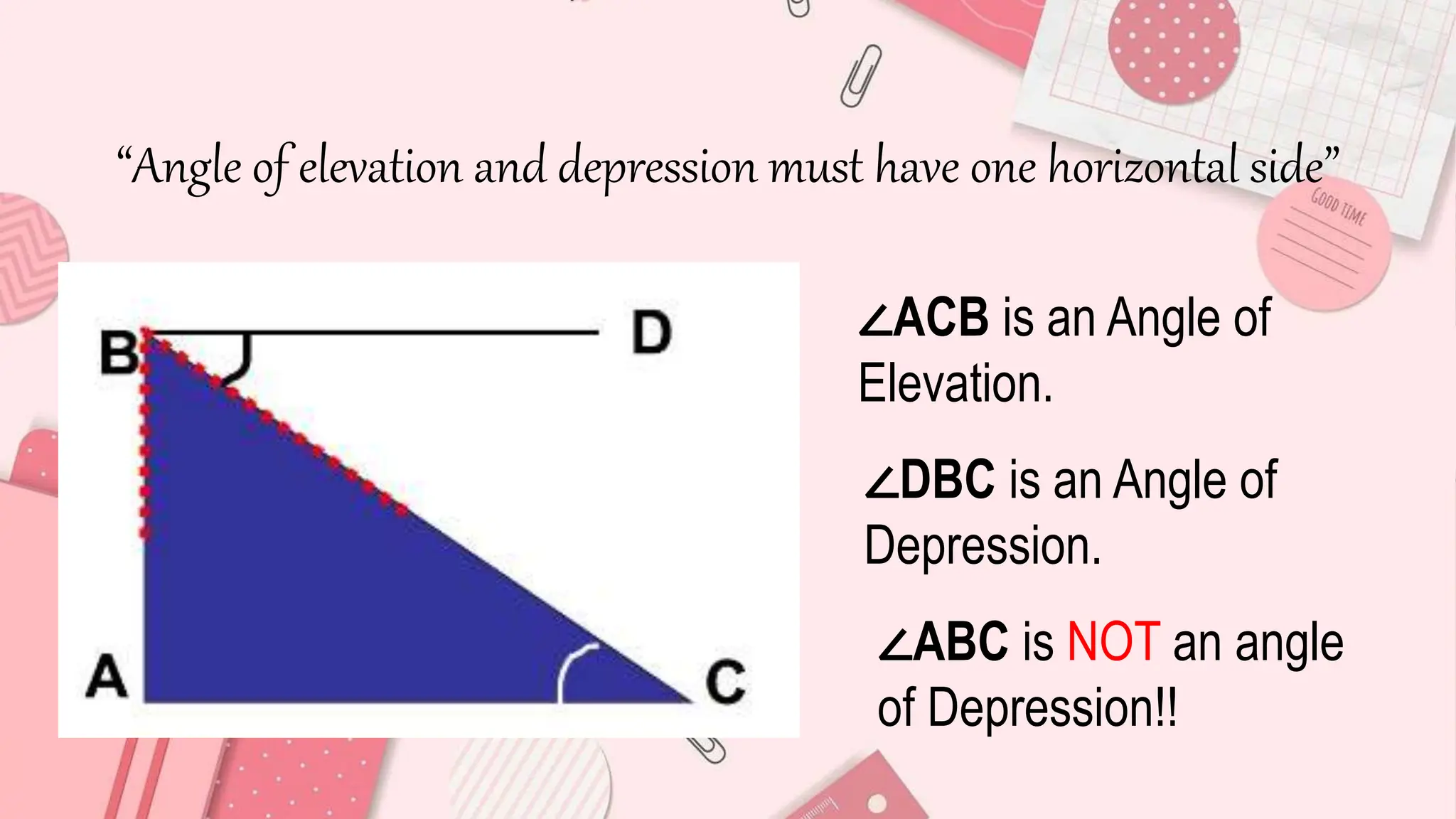
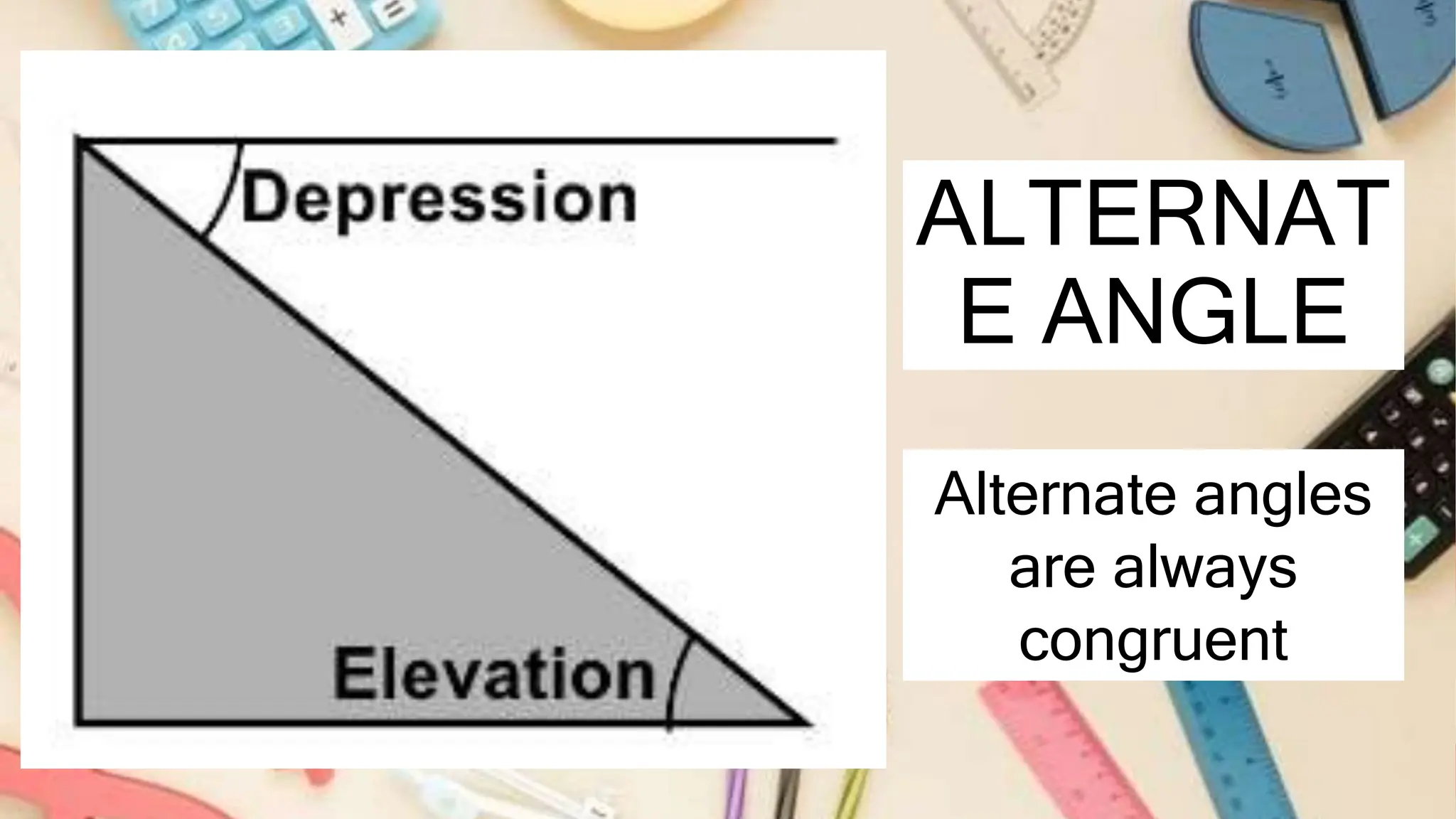
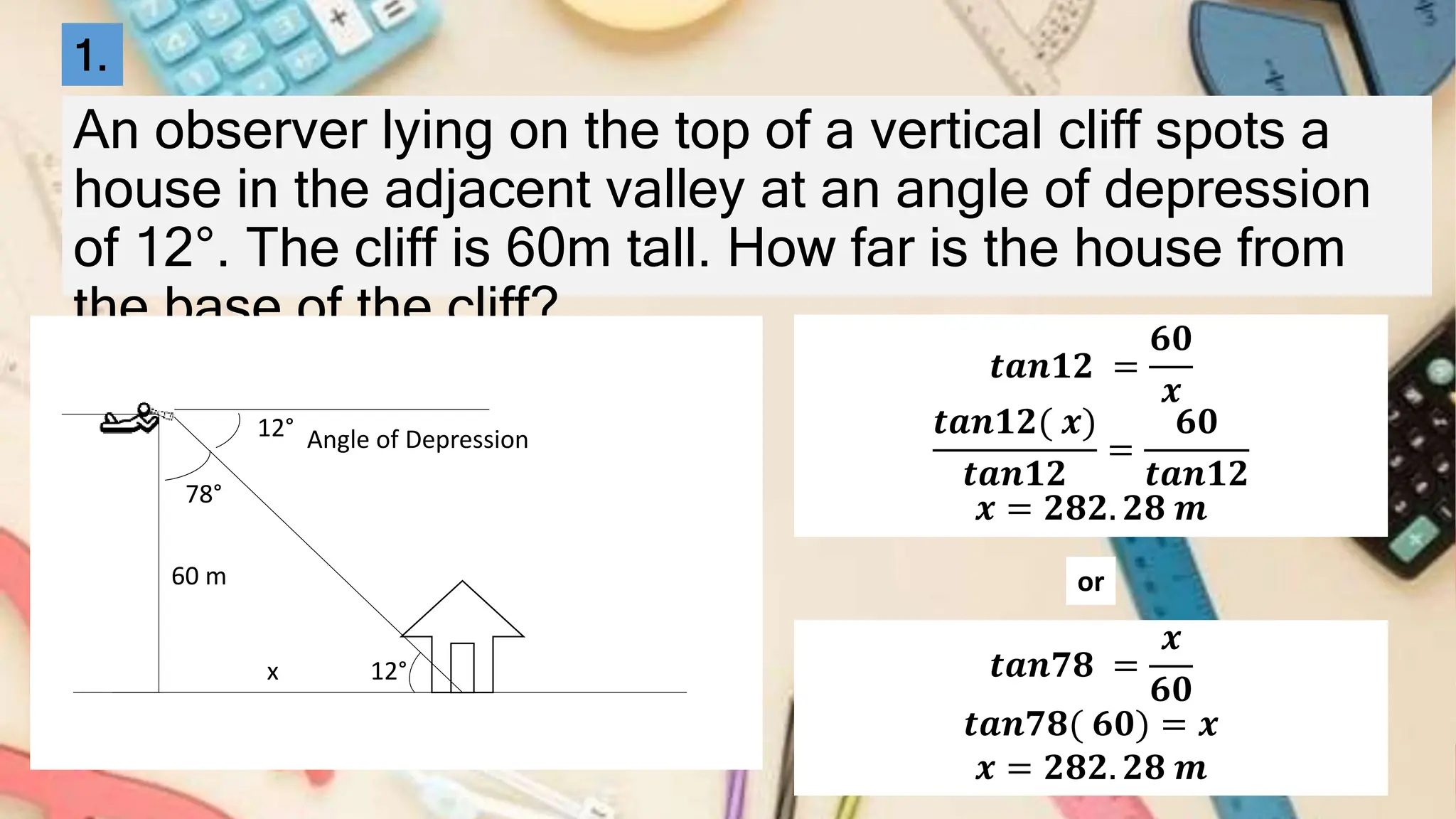
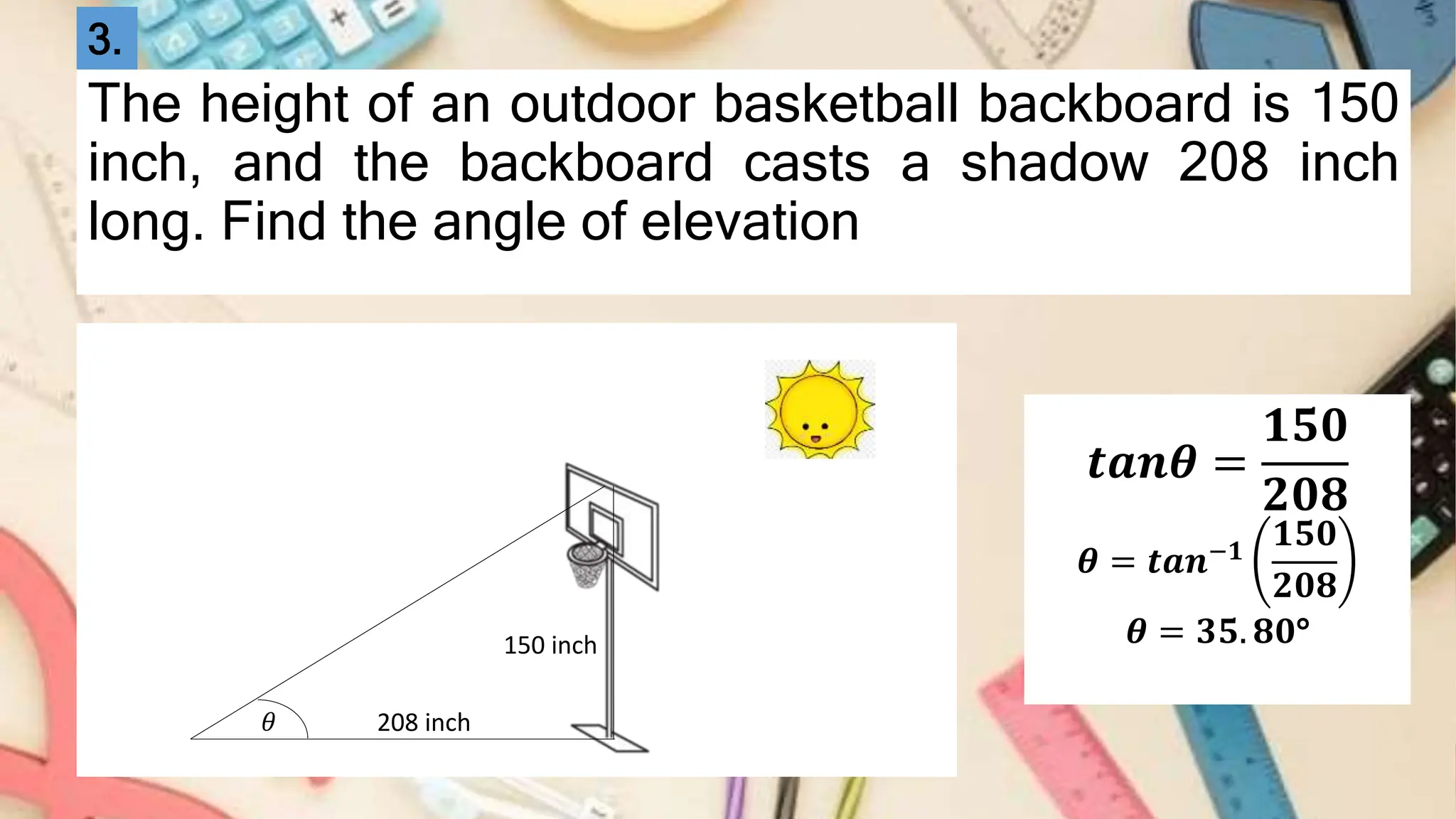
The document explains the concepts of angles of elevation and depression, including their definitions, applications in real-life situations, and methods for solving related problems. It outlines the steps for problem-solving, the importance of these angles in fields like physics and environmental science, and provides examples for understanding and calculating these angles. The lesson emphasizes the significance of visualizing scenarios and using trigonometric principles to derive the required measurements.

1. Angles of Elevation
and Depression

2. OBJECTIVES:
1. distinguish the difference between angle of
elevation and depression.
2. solve problems involving angles of elevation and
depression.
3. appreciate the importance of angles of elevation
and depression in solving problems in real life
situation.
At the end of this lesson, student will be able to:

4. ANGLE OF ELEVATION
The angle of elevation is
the angle formed by a
horizontal line and the
line of sight up to an
object when the image of
an object is located above
the horizontal line.

5. ANGLE OF DEPRESSION
The angle of
depression is the angle
formed by a horizontal
line and the line of sight
down to an object when
the image of an object
is located beneath the
horizontal line.

6. Angle of elevation and depression:

9. “Angle of elevation and depression must have one horizontal side”

10. “Angle of elevation and depression must have one horizontal side”
∠ACB is an Angle of
Elevation.
∠DBC is an Angle of
Depression.
∠ABC is NOT an angle
of Depression!!

11. NAMING ANGLE OF
ELEVATION AND
DEPRESSION
1
5
2
3
4
6
Angle of Depression
Angle of Elevation
Angle of Depression
Angle of Elevation
NOT AN ANGLE OF DEPRESSION
NOTE:
*Angle of elevation and depression always have a horizontal line and line of sight
(diagonal line).
*To identify whether an angle is an angle of elevation and depression, check whether
the line of sight is above or below the horizontal line.

12. ALTERNAT
E ANGLE
Alternate angles
are always
congruent

13. Application of Angles of Elevation and Depression
in Real Life
Physics:
Knowledge of angles
of elevation and
depression is crucial in
mechanics, optics, and
projectile motion.
Understanding how
angles affect the
motion of objects helps
in predicting
trajectories and forces.

14. Application of Angles of Elevation and Depression
in Real Life
Environmental
Science:
In studies like
ecosystem mapping
and surveying, angles
are used to measure
heights of trees,
depths of valleys, and
other physical features
of the environment.

15. SOLVING PROBLEMS
INVOLVING ANGLES OF
ELEVATION AND DEPRESSION

17. How To Solve Word Problems That Involve Angle
Of Elevation Or Depression?
STEPS TO FOLLOW:
Step 1: Draw a sketch of the situation.
Step 2: Mark in the given angle of elevation or
depression.
Step 3: Use trigonometry to find the required missing
length.
SOH, CAH, TOA, CHO, SHA, CAO

18. An observer lying on the top of a vertical cliff spots a
house in the adjacent valley at an angle of depression
of 12°. The cliff is 60m tall. How far is the house from
the base of the cliff?
12°
60 m
x
Angle of Depression
12°
78°
𝒕𝒂𝒏𝟏𝟐 =
𝟔𝟎
𝒙
𝒕𝒂𝒏𝟏𝟐( 𝒙)
𝒕𝒂𝒏𝟏𝟐
=
𝟔𝟎
𝒕𝒂𝒏𝟏𝟐
𝒙 = 𝟐𝟖𝟐. 𝟐𝟖 𝒎
1.
𝒕𝒂𝒏𝟕𝟖 =
𝒙
𝟔𝟎
𝒕𝒂𝒏𝟕𝟖( 𝟔𝟎) = 𝒙
𝒙 = 𝟐𝟖𝟐. 𝟐𝟖 𝒎
or

19. A home owner is to construct a ramp to his front
door to make it wheelchair accessible. How long is
the ramp if the door is 4ft above the ground level
and the angle of elevation is 20°?
4ft
20°
x
𝒔𝒊𝒏𝟐𝟎° =
𝟒
𝒙
𝒔𝒊𝒏𝟐𝟎° (𝒙)
𝐬𝐢𝐧 𝟐𝟎°
=
𝟒
𝒔𝒊𝒏𝟐𝟎°
𝒙 = 𝟏𝟏. 𝟕𝟎𝒇𝒕
2.

20. The height of an outdoor basketball backboard is 150
inch, and the backboard casts a shadow 208 inch
long. Find the angle of elevation
150 inch
208 inch
𝜃
𝒕𝒂𝒏𝜽 =
𝟏𝟓𝟎
𝟐𝟎𝟖
𝜽 = 𝒕𝒂𝒏−𝟏
𝟏𝟓𝟎
𝟐𝟎𝟖
𝜽 = 𝟑𝟓. 𝟖𝟎°
3.

21. Discussion Questions
Do you think your knowledge of angles of elevation
and depression can help solve real life problems?
What are the advantages of knowing how to solve
for angles of elevation and depression?
What are the disadvantages of using angles of
elevation and depression?
What other problems do you think can be solved
by angles of elevation and depression?

22. EXERCISE
S

23. 1.

24. For a laser lightshow at an amusement park, the
laser beam directed from the top of a 30 ft building
to reflect an object that is 100 ft. away from a point
directly below the location of the laser. What is the
angle of depression from the laser to the reflecting
object?
30 ft
100 ft
𝜃
2.

25. ANSWERS

26. 𝒕𝒂𝒏𝟓𝟎 =
𝒙
𝟖𝟕
𝒙 = 𝒕𝒂𝒏𝟓𝟎 𝟖𝟕
𝒙 = 𝟏. 𝟏𝟗𝟏𝟕 𝟖𝟕
𝒙 = 𝟏𝟎𝟑. 𝟔𝟖 𝒇𝒕.
1.

27. For a laser lightshow at an amusement park, the
laser beam directed from the top of a 30 ft building
to reflect an object that is 100 ft. away from a point
directly below the location of the laser. What is the
angle of depression from the laser to the reflecting
object?
30 ft
100 ft
𝜃
2.
𝒕𝒂𝒏𝜽 =
𝟑𝟎
𝟏𝟎𝟎
𝜽 = 𝒕𝒂𝒏−𝟏
𝟑𝟎
𝟏𝟎𝟎
𝒙 = 𝟏𝟔. 𝟕𝟎°

28. INDIVIDUAL
ASSESSMEN
T

29. From the top of a barn 5.3 m high, you
see a cat on the ground at 55° angle of
depression. How many meters must a
cat walk to reach the barn?
1.

30. With the sun, a girl √5 m tall cast a 2 m
shadow. Find the angle of elevation
from the tip of the shadow to the sun.
2.

31. A vertical pole 10 feet tall makes a
shadow 6 feet long on level ground.
What is the angle (to the nearest
degree) which the rays of the sun
make with the ground?
3.

32. ANSWERS

33. From the top of a barn 5.3 m high, you
see a cat on the ground at 55° angle of
depression. How many meters must a
cat walk to reach the barn?
1.
55°
5.3 m
X
55°
𝒕𝒂𝒏𝟓𝟓° =
𝟓. 𝟑
𝒙
𝒕𝒂𝒏𝟓𝟓( 𝒙)
𝒕𝒂𝒏𝟓𝟓
=
𝟓. 𝟑
𝒕𝒂𝒏𝟓𝟓
𝒙 = 𝟑. 𝟕𝟏 𝒎

34. With the sun, a girl √5 m tall cast a 2 m
shadow. Find the angle of elevation
from the tip of the shadow to the sun.
2.
𝜃
5 m
2 m
𝒕𝒂𝒏𝜽 =
𝟓
𝟐
𝜽 = 𝒕𝒂𝒏−𝟏
𝟓
𝟐
𝜽 = 𝟒𝟖. 𝟏𝟗°

35. A vertical pole 10 feet tall makes a
shadow 6 feet long on level ground.
What is the angle (to the nearest
degree) which the rays of the sun
make with the ground?
3.
𝜃
10 ft
6 ft
𝒕𝒂𝒏𝜽 =
𝟏𝟎
𝟔
𝜽 = 𝒕𝒂𝒏−𝟏
𝟏𝟎
𝟔
𝜽 = 59.04°