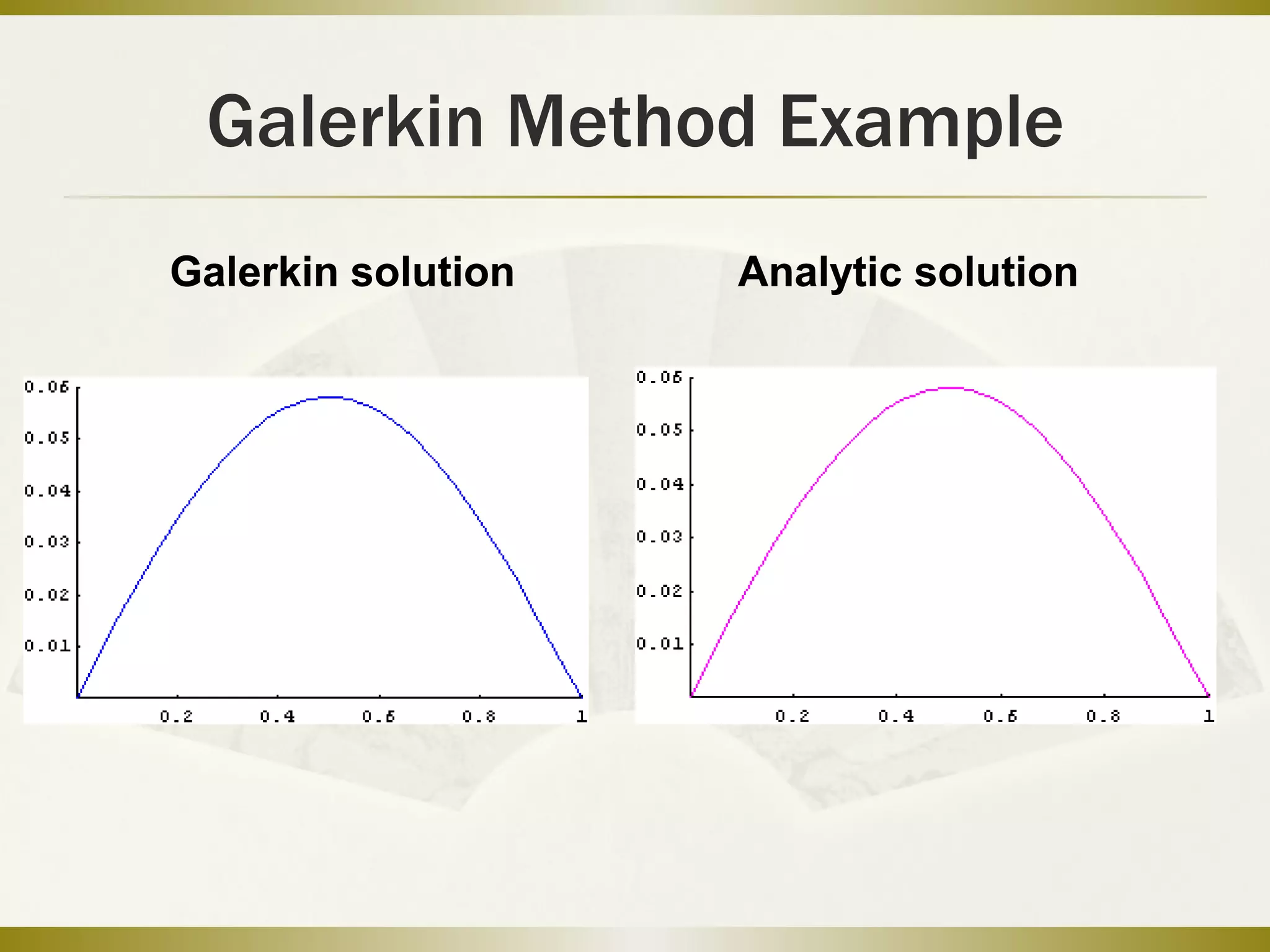
This document discusses the Galerkin method for solving differential equations. It begins by introducing how engineering problems can be expressed as differential equations with boundary conditions. It then explains that the Galerkin method uses an approximation approach to find the function that satisfies the equations. The key steps of the Galerkin method are to introduce a trial solution as a linear combination of basis functions, choose weight functions, take the inner product of the residual and weight functions to generate a system of equations for the unknown coefficients, and solve this system to obtain the approximate solution. An example of applying the Galerkin method to solve a second order differential equation is also provided.

1. Computational Engineering
Galerkin Method
Yijian Zhan
Ning Ma

2. Galerkin Method
 Engineering problems: differential
equations with boundary conditions.
Generally denoted as: D(U)=0; B(U)=0
 Our task: to find the function U which
satisfies the given differential equations
and boundary conditions.
 Reality: difficult, even impossible to solve
the problem analytically

3. Galerkin Method
 In practical cases we often apply
approximation.
 One of the approximation methods:
Galerkin Method, invented by Russian
mathematician Boris Grigoryevich Galerkin.

4. Galerkin Method
Related knowledge
 Inner product of functions
 Basis of a vector space of functions

5. Galerkin Method
Inner product
 Inner product of two functions in a certain
domain:
shows the inner
product of f(x) and g(x) on the interval [ a,
b ].
*One important property: orthogonality
If , f and g are orthogonal to each
other;
**If for arbitrary w(x), =0, f(x) 0
, ( ) ( )
b
a
f g f x g x dx  
, 0f g 
,w f  

6. Galerkin Method
Basis of a space
 V: a function space
 Basis of V: a set of linear independent
functions
Any function could be uniquely
written as the linear combination of the
basis:
0{ ( )}i iS x 

( )f x V
0
( ) ( )j j
j
f x c x


 

7. Galerkin Method
Weighted residual methods
 A weighted residual method uses a finite
number of functions .
 The differential equation of the problem is
D(U)=0 on the boundary B(U), for example:
on B[U]=[a,b].
where “L” is a differential operator and “f”
is a given function. We have to solve the
D.E. to obtain U.
0{ ( )}n
i ix 
( ) ( ( )) ( ) 0D U L U x f x  

8. Galerkin method
Weighted residual
 Step 1.
Introduce a “trial solution” of U:
to replace U(x)
: finite number of basis functions
: unknown coefficients
* Residual is defined as:
0
1
( ) ( ) ( )
n
j j
j
U u x x c x 

   
jc
( )j x
( ) [ ( )] [ ( )] ( )R x D u x L u x f x  

9. Galerkin Method
Weighted residual
 Step 2.
Choose “arbitrary” “weight functions” w(x),
let:
With the concepts of “inner product” and
“orthogonality”, we have:
The inner product of the weight function
and the residual is zero, which means that
the trial function partially satisfies the
problem.
So, our goal: to construct such u(x)
, ( ) , ( ) ( ){ [ ( )]} 0
b
a
w R x w D u w x D u x dx   

10. Galerkin Method
Weighted residual
 Step 3.
Galerkin weighted residual method:
choose weight function w from the basis
functions , then
These are a set of n-order linear
equations. Solve it, obtain all of the
coefficients .
j
0
1
, [ ( )] ( ){ [ ( ) ( )]} 0
nb
j j j ja
j
w R D u dx x D x c x dx   

     
jc

11. Galerkin Method
Weighted residual
 Step 4.
The “trial solution”
is the approximation solution we want.
0
1
( ) ( ) ( )
n
j j
j
u x x c x 

  

12. Galerkin Method Example
 Solve the differential equation:
with the boundary condition:
( ( )) ''( ) ( ) 2 (1 ) 0D y x y x y x x x    
(0) 0, (1) 0y y 

13. Galerkin Method Example
 Step 1.
Choose trial function:
We make n=3, and
0
1
( ) ( ) ( )
n
i i
i
y x x c x 

  
0
1
2 2
2
3 3
3
0,
( 1),
( 1)
( 1)
x x
x x
x x





 
 
 

14. Galerkin Method Example
 Step 2.
The “weight functions” are the same as
the basis functions
Step 3.
Substitute the trial function y(x) into
i
0
1
, [ ( )] ( ){ [ ( ) ( )]} 0
nb
j j j ja
j
w R D u dx x D x c x dx   

     

15. Galerkin Method Example
 Step 4.
i=1,2,3; we have three equations with
three unknown coefficients1 2 3, ,c c c
31 2
31 2
31 2
43 51
0
15 10 84 315
615 111
0
70 84 630 13860
734 611
0
315 315 13860 60060
cc c
cc c
cc c
    
   
    

16. Galerkin Method Example
 Step 5.
Solve this linear equation set, get:
Obtain the approximation solution
1
2
3
1370
0.18521
7397
50688
0.185203
273689
132
0.00626989
21053
c
c
c
   
 
   
3
1
( ) ( )i i
i
y x c x

 

17. Galerkin Method Example
GalerkinGalerkin solutionsolution Analytic solutionAnalytic solution

18. References
 1. O. C. Zienkiewicz, R. L. Taylor, Finite
Element Method, Vol 1, The Basis, 2000
 2. Galerkin method, Wikipedia:
http://en.wikipedia.org/wiki/Galerkin_method#cite_note-BrennerScott-1