FUZZY ARITHMETIC OPERATIONS ON DIFFERENT FUZZY NUMBERS AND THEIR VARIOUS FUZZY DEFUZZIFICATION METHODS

https://iaeme.com/Home/journal/IJARET 399 editor@iaeme.com
International Journal of Advanced Research in Engineering and Technology (IJARET)
Volume 10, Issue 1, January-February 2019, pp.399-412, Article ID: IJARET_10_01_041
Available online at https://iaeme.com/Home/issue/IJARET?Volume=10&Issue=1
ISSN Print: 0976-6480 and ISSN Online: 0976-6499
DOI: https://doi.org/10.34218/IJARET.10.1.2019.041
© IAEME Publication Scopus Indexed
FUZZY ARITHMETIC OPERATIONS ON
DIFFERENT FUZZY NUMBERS AND THEIR
VARIOUS FUZZY DEFUZZIFICATION
METHODS
V. Vanitha
Lecturer, Department of Mathematics, Tamilnadu Polytechnic College,
Madurai, Tamil Nadu, India
ABSTRACT
This paper describes fuzzy numbers, fuzzy arithmetic operations and their
defuzzification methods. First of all, we’ll look into the fundamental concept of fuzzy
numbers, and then the operations of fuzzy numbers. And also, we’ll look into the various
kinds of fuzzy numbers such as the triangular fuzzy number, trapezoidal fuzzy number
and pentagonal fuzzy number. Then we’ll also look into the various defuzzification
approaches of the above fuzzy numbers in this paper. In this study is to identify the
defuzzification formulas for various fuzzy numbers derived from research papers
published over the past few years. This paper presents the results of fuzzy ranking
applications used in fuzzy arithmetic operations very clearly and simply, as well as
highlighting key points in the use of fuzzy numbers. This paper discusses the importance
of pointing out the concepts of fuzzy arithmetic operations and their uses for fuzzy
ranking methods.
Key words: Triangular Fuzzy Number, Trapezoidal Fuzzy Number, Pentagonal Fuzzy
Number, Arithmetic Operations, Ranking methods.
Cite this Article: V. Vanitha, Fuzzy Arithmetic Operations on Different Fuzzy
Numbers and their Various Fuzzy Defuzzification Methods, International Journal of
Advanced Research in Engineering and Technology (IJARET), 10(1), 2019,
pp. 399-412.
https://iaeme.com/Home/issue/IJARET?Volume=10&Issue=1
1. INTRODUCTION
In 1975, Hutton, B [HU] & Rodabaugh, SE [Rod] introduced a fuzzy number. A fuzzy number
is the fundamental precept of the fuzzy set theory we typically use. It is chosen from the default
fuzzy set of all real numbers. Like standard numbers, fuzzy sets have been either positive or
negative, where the whole space is symmetrically empty. The linguistic form is often selected
to address the fuzzy number, which includes slightly, quietly. Calculations with fuzzy numbers
allow parameters, properties, geometry, and initial conditions to be inserted into uncertainty. In

Fuzzy Arithmetic Operations on Different Fuzzy Numbers and their Various Fuzzy
Defuzzification Methods
the literature on fuzzy sets, Zadeh (1965) notes that granulation plays a part in human cognition.
Membership functions are structured to represent individual and subjective human experiences
as part of a fuzzy set. A fuzzy set has several functions of membership, known as operations
from a well-defined universe. X with an interval between units, 0 to 1, as seen in the following
equation:
: [0,1]
A X
 →
The degree of notification for a vague class with an infinite set of range values between 0
and 1. The notification level for fuzzy numbers with an infinite set of range values between 0
and 1 is specified by the membership function. Fuzzy numbers play a crucial role in many fields
in computation, communications products engineering, scientific testing, decision-making,
approximate reasoning, and optimization.
2. PRELIMINARIES
2.1. Definition (Fuzzy Set)
A membership function maps the components of a domain space or universe of discourse X to
the unit interval [0,1] to define a fuzzy set.( i.e)  
1
,
0
: →
X
A




2.2. Definition (Fuzzy number)
A fuzzy number A

is a fuzzy set with a membership function ( )
x
A

 that meets the following
condition.
1. ( )
x
A

 is convex
2. ( )
x
A

 is regular
3. ( )
x
A

 is piecewise continuous
3. TRIANGULAR FUZZY NUMBER
3.1. Definition (Triangular fuzzy number)
It is a fuzzy number represented with three points as follows: ( )
, ,
A l m n
= this representation
is interpreted as membership functions (Fig 1). [1], [2], [5], [10]-[11],[15]
( )
0,
,
( )
,
0,
A
l x
x l
l x m
m l
x
n x
m x n
n m
n x





−

 
 −

= 
 −
 
 −


 

Now if you get crisp interval by  −cut operation, interval A shall be obtained as follows
[0,1]

  .

V. Vanitha
From,
( ) ( )
,
l l n n
m l n m
 
 
− −
= =
− −
We get, ( )
( )
l m l l


= − +
( )
( )
n n m n


= − − +
Thus,
( ) ( )
,
A l n
 
  
=  
( ) , ( )
A m l l n m n
  
= − + − − +
 
 
Figure 1 Triangular Fuzzy Number ( )
, ,
=
A l m n
3.2. Operation of Triangular Fuzzy Number
Suppose A and B are two triangular fuzzy numbers defined as
( ) ( )
1 1 1 2 2 2
, , , , ,
A l m n B l m n
= =
, 1 1 1 2 2 2
, , , , ,
l m n l m n
 R
Then
Addition
( )
1 2 1 2 1 2
( ) , ,
A B l l m m n n
+ = + + +
Subtraction
( )
1 2 1 2 1 2
( ) , ,
A B l n m m n l
− = − − −
Multiplication
( )
1 2 1 2 1 2
( ) , ,
A B l l m m n n
 =
Here 1 1 1 2 2 2
, , , , ,
l m n l m n are all non-zero positive real numbers.
3.3. Defuzzification Methods for Triangular Fuzzy Numbers
Many types of ranking procedures have 'Triangular fuzzy numbers.' All the rankings listed here
have been discovered over the past few years for 'Triangular fuzzy numbers' and compiled from
studying various research papers. Only the most important of them are listed here.

Let ( )
, ,
A l m n
= be a Triangular fuzzy number. Then the various ranking methods for the
TFN is followed as,
−
 Cut for Triangular Fuzzy Numbers
( )
,
, ( )
L U
A a a
m l l n m n
  
 
 
=  
= − + − − +
 
 
Robust Ranking for Triangular Fuzzy Numbers
( )
1
0
( ) 0.5 ,
L U
R A a a d
  
= 
Where ( )
,
L U
a a
  is  − cut of triangular fuzzy number A determines the Robust’s
Ranking Index.
Sub interval Average method for Triangular Fuzzy Numbers
( )
( )
4
, ,
12
l m n
R l m n
+ +
=
Centroidal approach for Triangular Fuzzy Numbers
( )
2 14 2 7
, , ;
6 6
+ +
   
= 
   
   
l m n w
C l m n w
3.4. Example
Consider two triangular fuzzy number ( )
4
,
2
,
0
=
A and ( )
6
,
4
,
2
=
B . Apply the fuzzy arithmetic
operations and fuzzy defuzzification methods under fuzzy arithmetic situation.
Table 1 Arithmetic Operations of Triangular Fuzzy Number
Addition
( )
1 2 1 2 1 2
( ) , ,
A B l l m m n n
+ = + + +
( )
4
,
2
,
0
=
A
( )
6
,
4
,
2
=
B
( ) ( )
10
,
6
,
2
=
+ B
A
Subtraction
( )
1 2 1 2 1 2
( ) , ,
A B l n m m n l
− = − − −
( )
4
,
2
,
0
=
A
( )
6
,
4
,
2
=
B
( ) ( )
2
,
2
,
6 −
−
=
− B
A
Multiplication
( )
1 2 1 2 1 2
( ) , ,
A B l l m m n n
 =
( )
4
,
2
,
0
=
A
( )
6
,
4
,
2
=
B
( ) ( )
10
,
8
,
0
=
 B
A
Division 1 1 1
2 2 2
( ) , ,
l m n
A B
n m l
 
 =  
 
( )
4
,
2
,
0
=
A
( )
6
,
4
,
2
=
B
( ) 





=

2
4
,
2
1
,
0
B
A
Let us find out the defuzzification methods for triangular fuzzy numbers

V. Vanitha
i. Alpha cut for Triangular fuzzy number
( )
,
, ( )
L U
A a a
m l l n m n
  
 
 
=  
= − + − − +
 
 
Table 2 Alpha cut for Triangular fuzzy number under fuzzy arithmetic operation
Addition ( ) ( )
10
,
6
,
2
=
+ B
A ( ) ( )
10
4
,
2
4 +
−
+
=
+ 

B
A
Subtraction ( ) ( )
2
,
2
,
6 −
−
=
− B
A ( ) ( )
2
8
,
6
4 +
−
−
=
− 

B
A
Multiplication ( ) ( )
10
,
8
,
0
=
 B
A ( ) ( )
10
10
,
0
8 +
−
+
=
 

B
A
ii. Robust Ranking for Triangular Fuzzy Numbers
( )
1
0
( ) 0.5 ,
L U
R A a a d
  
=  Where ( )
,
L U
a a
  is  − cut of triangular fuzzy number A
determines the Robust’s Ranking Index.
Table 3 Robust ranking for Triangular fuzzy number under fuzzy arithmetic operation
Addition ( ) ( ) ( ) 6
10
4
,
2
4
5
.
0
10
,
6
,
2
1
0
=
+
−
+
=
=
+  

 d
B
A ( ) 6
=
+ B
A
Subtraction ( ) ( ) ( ) 3
2
8
,
6
4
5
.
0
2
,
2
,
6
1
0
−
=
+
−
−
=
−
−
=
−  

 d
B
A ( ) 3
−
=
− B
A
Multiplication ( ) ( ) ( ) 9
10
10
,
0
8
5
.
0
10
,
8
,
0
1
0
=
+
−
+
=
=
  

 d
B
A ( ) 9
=
 B
A
iii. Sub interval Average method for Triangular Fuzzy Numbers
( )
( )
4
, ,
12
l m n
R l m n
+ +
=
Table 4 Sub interval average method for Triangular fuzzy number under fuzzy arithmetic operation
Addition ( ) 6
=
+ B
A
Subtraction ( ) 2
−
=
− B
A
Multiplication ( ) 6
=
 B
A
iv. Centroid ranking approach for Triangular Fuzzy Numbers
( )
2 14 2 7
, , ;
6 6
+ +
   
= 
   
   
l m n w
C l m n w
Table 5 Centroid ranking for Triangular fuzzy number under fuzzy arithmetic operation
Addition ( ) 21
=
+ B
A
Subtraction ( ) 7
−
=
− B
A
.
25
=
 B
A

4. TRAPEZOIDAL FUZZY NUMBER
4.1. Definition (Trapezoidal fuzzy number)
We can define trapezoidal fuzzy number A as ( )
, , ,
A k l m n
= the membership function of this
fuzzy number will be interpreted as follows (Fig. 2). [1], [2], [5], [10]-[11], [15]
( )
0,
,
( ) 1,
,
0,
A
x k
x k
k x l
l k
x l x m
n x
m x n
n m
x n





−

 
 −



=  



−
  
 −


 

Figure 2 Trapezoidal Fuzzy Number ( )
, , ,
A k l m n
=
 − Cut interval for this shape is written below.
 
0,1

  .
( ) ( )
,
A l k k n m n
  
= − + − − +
 
 
When l m
= , the trapezoidal fuzzy number coincides with triangular one.
4.2. Operation of Trapezoidal Fuzzy Number
Let A and B are two non-negative trapezoidal fuzzy numbers defined as

V. Vanitha
( ) ( )
1 1 1 1 2 2 2 2
, , , , , , ,
= =
A k l m n B k l m n ,
1 1 1 1 2 2 2 2
, , , , , , ,
 
k l m n k l m n R .
Then
Addition
( ) ( )
( )
1 1 1 1 2 2 2 2
1 2 1 2 1 2 1 2
( ) , , , ( ) , , ,
, , ,
+ = +
= + + + +
A B k l m n k l m n
k k l l m m n n
Subtraction
( ) ( )
( )
1 1 1 1 2 2 2 2
1 2 1 2 1 2 1 2
( ) , , , ( ) , , ,
, , ,
− = −
= − − − −
A B k l m n k l m n
k n l m m l n k
Multiplication
( ) ( )
( )
1 1 1 1 2 2 2 2
1 2 1 2 1 2 1 2
( ) , , , ( ) , , ,
, , ,
 = 
=
A B k l m n k l m n
k k l l m m n n
Here 1 1 1 1 2 2 2 2
, , , , , , ,
k l m n k l m n are all non-zero positive real numbers.
4.3. Ranking Methods for Trapezoidal Fuzzy Number
There are 'Trapezoidal fuzzy numbers' for several forms of ranking procedures. Even the most
important of them here Over the past few years, all the rankings listed here have been found for
'Trapezoidal fuzzy numbers' and collected by reviewing different research papers.
Let ( )
, , ,
=
A k l m n be a Trapezoidal fuzzy number. Then the various ranking methods for
the TFN is followed as,
−
 cut for Trapezoidal Fuzzy Numbers
( )
( ) ( )
 
L
a ,
,
U
A a
l k k n n m
 
 
=
= − + − −
Robust Ranking for Triangular Fuzzy Numbers
( )
1
0
( ) 0.5 ,
  
= 
L U
R A a a d
Where ( )
,
L U
a a
  is  − cut of trapezoidal fuzzy number Adetermines the Robust’s
Ranking Index.
Sub interval Average method for Trapezoidal Fuzzy Numbers
( )
( )
5
, , ,
20
+ + +
=
k l m n
R k l m n

Centroidal approach for Trapezoidal Fuzzy Numbers
( )
2 7 7 7
, , , ;
6 6
+ + +
   
= 
   
   
k l m n w
C k l m n w
4.4. Example
Consider two trapezoidal fuzzy number ( ) ( )
5,8,11,12
B
a
7
,
6
,
5
,
3 =
=
A . Apply the
fuzzy arithmetic operations and fuzzy defuzzification methods under fuzzy arithmetic situation.
Table 6 Arithmetic Operations of Triangular Fuzzy Number
Addition
( ) ( ) ( ) ( )
( )
2
1
2
1
2
1
2
1
2
2
2
2
1
1
1
1
n
,
m
,
l
,
k
,
,
,
k
,
,
,
n
m
l
k
n
m
l
n
m
l
k
B
A
+
+
+
+
=
+
=
+
( ) ( )
19
,
17
,
13
,
8
=
+ B
A
Subtraction
( ) ( )
( )
1 1 1 1 2 2 2 2
1 2 1 2 1 2 1 2
( ) , , , ( ) , , ,
, , ,
− = −
= − − − −
A B k l m n k l m n
k n l m m l n k
( ) ( )
2
,
2
,
6
,
9 −
−
−
=
− B
A
Multiplication
( ) ( )
( )
1 1 1 1 2 2 2 2
1 2 1 2 1 2 1 2
( ) , , , ( ) , , ,
, , ,
 = 
=
A B k l m n k l m n
k k l l m m n n
( ) ( )
84
,
66
,
40
,
15
=
 B
A
Let us find out the defuzzification methods for trapezoidal fuzzy numbers
i. Alpha cut for Trapezoidal Fuzzy Numbers
( )
( ) ( )
 
L
a ,
,
U
A a
l k k n n m
 
 
=
= − + − −
Table 7 Alpha cut for Trapezoidal fuzzy number under fuzzy arithmetic operation
Addition ( ) ( )
19
,
17
,
13
,
8
=
+ B
A ( ) ( )

 2
19
,
8
5 −
+
=
+ B
A
Subtraction ( ) ( )
2
,
2
,
6
,
9 −
−
−
=
− B
A ( ) ( )

 4
2
,
9
3 −
−
=
− B
A
84
,
66
,
40
,
15
=
 B
A ( ) ( )

 18
84
,
15
25 −
+
=
 B
A
ii. Robust Ranking for Trapezoidal Fuzzy Numbers
( )
1
0
( ) 0.5 ,
  
= 
L U
R A a a d Where ( )
,
L U
a a
  is  − cut of trapezoidal fuzzy number A
determines the Robust’s Ranking Index.

V. Vanitha
Table 8 Robust ranking method for Trapezoidal fuzzy number under fuzzy arithmetic operation
Addition ( ) ( ) 

 d
B
A  −
+
=
+
1
0
2
19
,
8
5
5
.
0 ( ) 250
.
14
=
+ B
A
Subtraction
( ) ( ) 

 d
B
A  −
−
=
−
1
0
4
2
,
9
3
5
.
0 ( ) 750
.
3
−
=
− B
A
Multiplication ( ) ( ) 

 d
B
A  −
+
=

1
0
18
84
,
15
25
5
.
0 ( ) 250
.
51
=
 B
A
iii. Sub interval Average method for Trapezoidal Fuzzy Numbers
( )
( )
5
, , ,
20
+ + +
=
k l m n
R k l m n
Table 9 Sub interval average method for Triangular fuzzy number under fuzzy arithmetic operation
Addition ( ) 250
.
14
=
+ B
A
Subtraction ( ) 750
.
3
−
=
− B
A
.
51
=
 B
A
iv. Centroid approach for Trapezoidal Fuzzy Numbers
( )
2 7 7 7
, , , ;
6 6
+ + +
   
= 
   
   
k l m n w
C k l m n w
Table 10 Centroid method for Triangular fuzzy number under fuzzy arithmetic operation
Addition ( ) 639
.
47
=
+ B
A
Subtraction ( ) 000
.
14
−
=
− B
A
.
166
=
 B
A
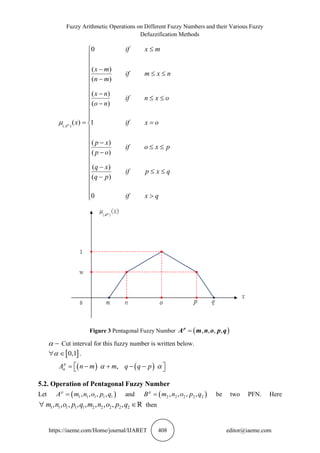
5. PENTAGONAL FUZZY NUMBER
5.1. Definition (Pentagonal Fuzzy Number)
A fuzzy number ( )
, , , ,
p
A m n o p q
= is called a pentagonal fuzzy number (PFN) should satisfy
the following condition [1], [7]-[9], [12]-[15]
In the interval  
0,1 , ( )
( )
p
A
x
 is a continuous function
 
,
m n and  
,
n o is a continuous function and ( )
( )
p
A
x
 is strictly increasing
 
,
o p and  
,
p q is a continuous function and ( )
( )
p
A
x
 is strictly decreasing
The membership function of this fuzzy number will be interpreted as follows (Fig 4.6).

( )
0
( )
( )
( )
( )
( ) 1
( )
( )
( )
( )
0
p
A
if x m
x m
if m x n
n m
x n
if n x o
o n
x if x o
p x
if o x p
p o
q x
if p x q
q p
if x q





−

 
 −


−
  
 −



= =



−
  
 −

 −
  
−






Figure 3 Pentagonal Fuzzy Number ( )
, , , ,
=
p
A m n o p q
 − Cut interval for this fuzzy number is written below.
 
0,1

  .
( ) ( )
,
p
A n m m q q p
  
= − + − −
 
 
5.2. Operation of Pentagonal Fuzzy Number
Let ( )
1 1 1 1 1
, , , ,
p
A m n o p q
= and ( )
2 2 2 2 2
, , , ,
p
B m n o p q
= be two PFN. Here
1 1 1 1 1 2 2 2 2 2
, , , , , , , , ,
m n o p q m n o p q
 R then

V. Vanitha
Addition
( ) ( )
( )
1 1 1 1 1 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2
( ) , , , , ( ) , , , ,
= , , , ,
p p
A B m n o p q m n o p q
m m n n o o p p q q
+ = +
+ + + + +
Subtraction
( ) ( )
( )
1 1 1 1 1 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2
( ) , , , , ( ) , , , ,
= , , , ,
p p
m q n p o o p n q m
− = −
− − − − −
Multiplication
( ) ( )
( )
1 1 1 1 1 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2
( ) , , , , ( ) , , , ,
= , , , ,
p p
m m n n o o p p q q
 = 
5.3. Ranking Methods for Pentagonal Fuzzy Numbers
They are many 'Pentagonal Fuzzy Numbers' ranking procedures. All the rankings listed here
have been developed for 'Pentagonal Fuzzy Numbers' over the last few years and collected from
the consideration of different research papers. Just the most important of them are listed here.
Let ( )
, , , ,
p
A m n o p q
= be a Pentagonal fuzzy number. Then the various ranking methods
for the PFN is followed as,
−
 Cut for Pentagonal Fuzzy Numbers
( ) ( )
( ) ( ) ( )
,
,
p L U
A a a
n m m q q p
  
 
 
=  
= − + − −
 
 
Robust ranking method for Pentagonal Fuzzy Numbers
( ) ( )
 
1
0
, , , ,
1
( ) , ( )
2
p
R A R m n o p q
n m m q q p d
  
=
= − + − −

Sub interval Average method for Pentagonal Fuzzy Numbers
( ) ( )
( )
, , , ,
6
30
p
R A R m n o p q
m n o p q
=
+ + + +
=

Centroid approach for Pentagonal Fuzzy Numbers
( ) ( )
, , , , ;
3 4 3 6 2 4
18 9
p
R A R m n o p q w
m n o p q w
=
+ + + +
   
= 
   
   
5.4. Example
Consider two Pentagonal fuzzy numbers ( ) ( )
1,3,6,9,11
B
and
10
,
8
,
6
,
4
,
2 =
=
A . Apply the fuzzy
arithmetic operations and fuzzy defuzzification methods under fuzzy arithmetic situation.
Table 11 Arithmetic Operations of Pentagonal Fuzzy Number
Addition
( ) ( )
( )
1 1 1 1 1 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2
( ) , , , , ( ) , , , ,
= , , , ,
p p
m m n n o o p p q q
+ = +
+ + + + +
( ) ( )
21
,
17
,
12
,
7
,
3
=
+ B
A
Subtraction
( ) ( )
( )
1 1 1 1 1 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2
( ) , , , , ( ) , , , ,
= , , , ,
p p
m q n p o o p n q m
− = −
− − − − −
( ) ( )
9
,
5
,
0
,
5
,
9 −
−
=
− B
A
Multiplication
( ) ( )
( )
1 1 1 1 1 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2
( ) , , , , ( ) , , , ,
= , , , ,
p p
m m n n o o p p q q
 = 
( ) ( )
110
,
72
,
36
,
12
,
2
=
 B
A
Let us find out the defuzzification methods for trapezoidal fuzzy numbers
i. Alpha cut for Pentagonal Fuzzy Numbers
( ) ( )
( ) ( ) ( )
,
,
p L U
A a a
n m m q q p
  
 
 
=  
= − + − −
 
 
Table 12 Alpha cut method for Pentagonal fuzzy number under fuzzy arithmetic operation
Addition ( ) ( )
21
,
17
,
12
,
7
,
3
=
+ B
A ( ) ( )

 4
21
,
3
4 −
+
=
+ B
A
Subtraction ( ) ( )
9
,
5
,
0
,
5
,
9 −
−
=
− B
A ( ) ( )

 4
9
,
9
4 −
−
=
− B
A
110
,
72
,
36
,
12
,
2
=
 B
A ( ) ( )

 38
110
,
2
10 −
+
=
 B
A
ii. Robust ranking method for Pentagonal Fuzzy Numbers
( ) ( )
 
1
0
, , , ,
1
( ) , ( )
2
p
R A R m n o p q
n m m q q p d
  
=
= − + − −


V. Vanitha
Table 13 Robust ranking method for Pentagonal fuzzy number under fuzzy arithmetic operation
Addition ( ) ( ) 

 d
B
A  −
+
=
+
1
0
4
21
,
3
4
5
.
0 ( ) 12
=
+ B
A
Subtraction ( ) ( ) 

 d
B
A  −
−
=
−
1
0
4
9
,
9
4
5
.
0 ( ) 0
=
− B
A
Multiplication ( ) ( ) 

 d
B
A  −
+
=

1
0
38
110
,
2
10
5
.
0 ( ) 49
=
 B
A
iii. Sub interval Average method for Pentagonal Fuzzy Numbers
( ) ( )
( )
, , , ,
6
30
p
R A R m n o p q
m n o p q
=
+ + + +
=
Table 14 Sub interval average method for Pentagonal fuzzy number under fuzzy arithmetic operation
Addition ( ) 12
=
+ B
A
Subtraction ( ) 0
=
− B
A
.
46
=
 B
A
iv. Centroid approach for Pentagonal Fuzzy Numbers
( ) ( )
, , , , ;
3 4 3 6 2 4
18 9
p
R A R m n o p q w
m n o p q w
=
+ + + +
   
= 
   
   
Table 15 Centroid method for Pentagonal fuzzy number under fuzzy arithmetic operation
Addition ( ) 358
.
5
=
+ B
A
Subtraction ( ) 025
.
0
=
− B
A
.
20
=
 B
A
6. CONCLUSION
We've only considered fuzzy numbers and fuzzy arithmetic operations only throughout this
paper. We clarified quite well during this survey, and thus, the various types of fuzzy numbers
have developed in the previous few years and their different types of defuzzification systems.
This survey paper has been compiled very clearly for the possible purpose of developing fuzzy
numbers and its defuzzification methods for the future numerical evaluation system.

REFERENCES
[1] Dinagar, S., Kamalanathan, R., & Rameshan, N. (2017). Sub Interval Average Method for
Ranking of Linear Fuzzy Numbers. International Journal of Pure and Applied Mathematics,
114(6), 119-130.
[2] Dinagar, D. S., & Kamalanathan, S. (2017). Solving fuzzy linear programming problem using
new ranking procedures of fuzzy numbers. International Journal of Applications of Fuzzy Sets
and Artificial Intelligence, 7, 281-292.
[3] Dinagar, D. S., & Jeyavuthin, M. M. (2019). Distinct Methods for Solving Fully Fuzzy Linear
Programming Problems with Pentagonal Fuzzy Numbers. Journal of Computer and
Mathematical Sciences, 10(6), 1253-1260.
[4] Ganesh, A. H., Suresh, M., & Sivakumar, G. (2020). On solving fuzzy transportation problem
based on distance based defuzzification method of various fuzzy quantities using centroid.
Malaya Journal of Matematik (MJM), (1, 2020), 410-426.
[5] Hassanzadeh, R., Mahdavi, I., Mahdavi-Amiri, N., & Tajdin, A. (2018). An α-cut approach for
fuzzy product and its use in computing solutions of fully fuzzy linear systems. International
Journal of Mathematics in Operational Research, 12(2), 167-189.
[6] Kalpana, B., & Anusheela, N. (2018). Analysis of Fm/Fm/I Fuzzy Priority Queues Based On
New Approach of Ranking Fuzzy Numbers Using Centroid of Centroids. International Journal
of Pure and Applied Mathematics, 119(7), 457-465.
[7] Kamble, A. J. (2017). Some notes on Pentagonal fuzzy numbers. Int J Fuzzy Math Arch, 13,
113-121.
[8] Mondal, S. P., & Mandal, M. (2017). Pentagonal fuzzy number, its properties and application
in fuzzy equation. Future Computing and Informatics Journal, 2(2), 110-117.
[9] PraveenPrakash, A., & GeethaLakshmi, M. (2016). A Comparative Study-Optimal Path using
Trident and Sub-Trident Forms through Fuzzy Aggregation, Ranking and Distance Methods.
International Journal of Pure and Applied Mathematics, 109(10), 139-150.
[10] Ponnialagan, Dhanasekaran, JeevarajSelvaraj, and LakshmanaGomathiNayagamVelu. "A
complete ranking of trapezoidal fuzzy numbers and its applications to multi-criteria decision
making." Neural Computing and Applications 30, no. 11 (2018): 3303-3315.
[11] Selvam, P., Rajkumar, A., &Easwari, J. S. (2017). Ranking of pentagonal fuzzy numbers
applying incentre of centroids. International Journal of Pure and Applied Mathematics,
117(13), 165-174.
[12] Selvakumari, K., &Santhi, S. (2018). A Pentagonal Fuzzy Number Solving Fuzzy Sequencing
Problem. International Journal of Mathematics and its Application, 6(2-B), 207-211.
[13] Srinivasan, R., Nakkeeran, T., & Saveetha, G. Evaluation of fuzzy non-preemptive priority
queues in intuitionistic pentagonal fuzzy numbers using centroidal approach. Malaya Journal of
Matematik (MJM), (1, 2020), 427-430.
[14] Srinivasan, R., Saveetha, G., & Nakkeeran, T. (2020). Comparative study of fuzzy assignment
problem with various ranking. Malaya Journal of Matematik (MJM), (1, 2020), 431-434.
[15] Srinivasan, R., Nakkeeran, T., Renganathan, K. and Vijayan, V., The performance of pentagonal
fuzzy numbers in finite source queue models using Pascal’s triangular graded mean. Materials
Today: Proceedings, vol. 37, pp.947-949, 2021.

FUZZY ARITHMETIC OPERATIONS ON DIFFERENT FUZZY NUMBERS AND THEIR VARIOUS FUZZY DEFUZZIFICATION METHODS

More Related Content

What's hot

Similar to FUZZY ARITHMETIC OPERATIONS ON DIFFERENT FUZZY NUMBERS AND THEIR VARIOUS FUZZY DEFUZZIFICATION METHODS

More from IAEME Publication

Recently uploaded

FUZZY ARITHMETIC OPERATIONS ON DIFFERENT FUZZY NUMBERS AND THEIR VARIOUS FUZZY DEFUZZIFICATION METHODS