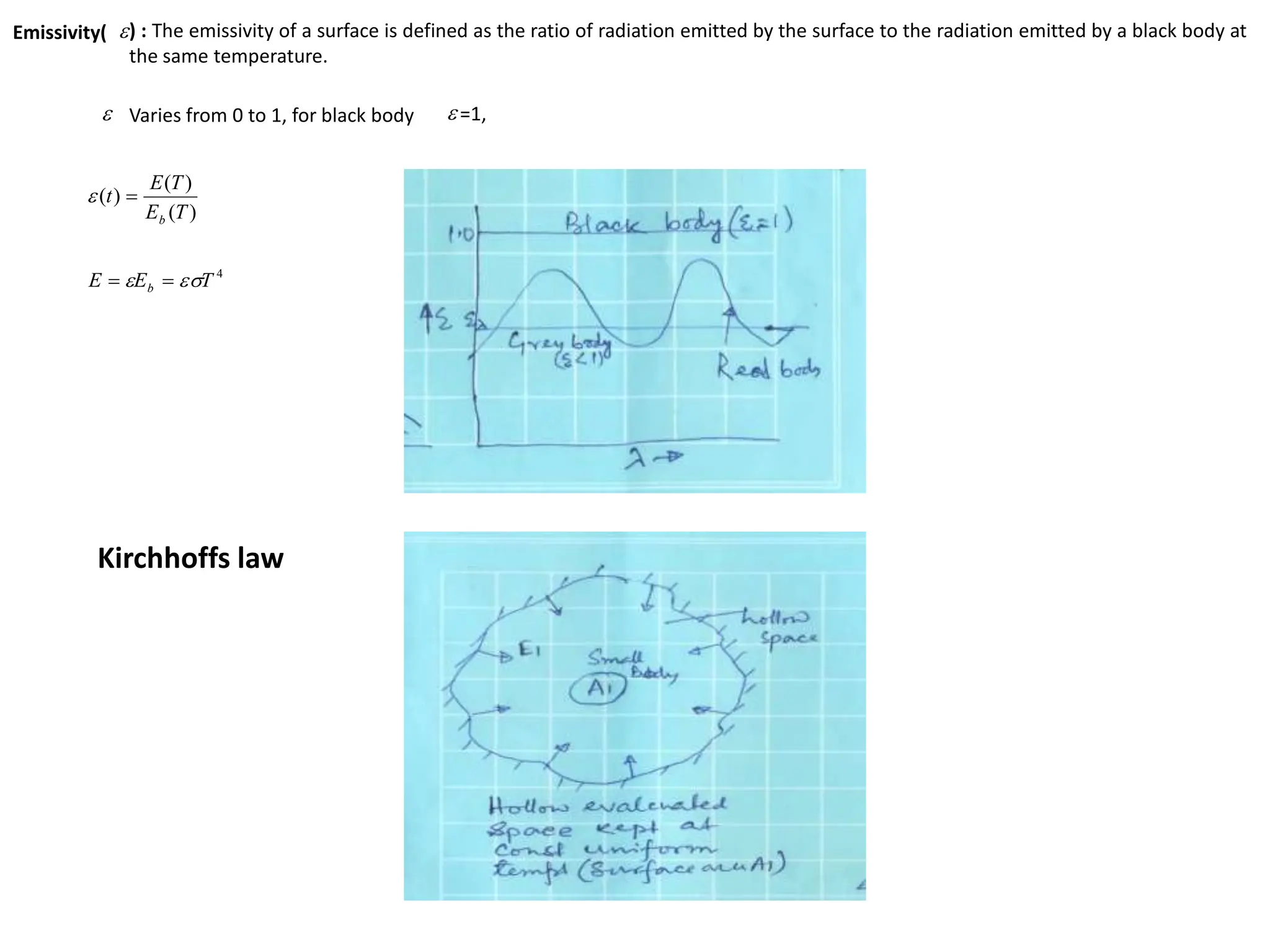
The document discusses fundamental concepts of radiation, including absorptivity, reflectivity, and transitivity of materials. It explains how a black body absorbs all incident radiation and introduces key laws like Stefan-Boltzmann law and Kirchhoff's law, emphasizing the relationship between emitted and absorbed radiation. Also mentioned are the concepts of emissive power, emissivity, and Wien's displacement law, which relate to the spectrum of thermal radiation emitted by bodies at different temperatures.

1. Radiation
?
Radiation

2. 0
.
1













Q
Q
Q
Q
Q
Q
r
a
t
REFLECTED
IS
WHICH
RADIATION
INCIDENT
OF
FRACTION
ABSORBED
IS
WHICH
RADIATION
INCIDENT
OF
FRACTION
D
TRANSMITTE
IS
WHICH
RADIATION
INCIDENT
OF
FRACTION






Absorptivity, Reflectivity, and transitivity
Any matter can absorb, emit and transmit radiant energy. Say Q is the total radiant energy incident upon a surface, some part of
radiant energy (Qa) will be absorbed, some part (Qr) is reflected and some part (Qt) is transmitted through the body. By energy balance,
Q=Qa+Qr+Qt
Q/Q=Qa/Q+Qr/Q+Qt/Q

3. 0
,
0
.
1
,
0 

 


0
.
1
,
0 

 


Black body: Black body is one which neither reflects nor transmits any part of the incident radiation but absorbs
all of it. For perfectly absorbing body,
In practice, a perfect black body does not exist. However its concept is very important.
Opaque body: When no incident radiation is transmitted through a body, called opaque body,
Most solids do not transmit any radiation are opaque. The reflectivity depends on the character of surface.
Therefore the absorptivity of an opaque body can be increased or decreased by appropriate surface treatment.
Roughening a solid surface means less reflectivity enhances absorptivity accordingly.
Surface type Properties
Opaque surface
White surface
Transparent surfaces
Black bodies
0


0
.
1
,
0 

 


0
.
1


0
.
1



4. Emissive power
If the radiation from a heated body is dispersed into a spectrum by a prism, it is found that the radiant energy is
distributed among various wavelengths.
Total emissive power of a body E, is defined as the total radiant energy emitted by the body E at a certain
temperature per unit time and per unit surface area at all wavelengths.
The monochromatic emissive power of a body

E is the radiant energy emitted by the body per unit time per unit surface area at a particular wavelength and
temperature.
The rate of emission of radiation by a body dependent upon the following factors:
• Temperature of surface
• Nature of surface
• Wavelength or frequency of radiation
4
T
Eb 

4
2
8
/
10
67
.
5 K
m
W




The radiation energy emitted by a black body per unit time and per unit surface area is given by
(W/m2) where is called Stefan-Boltzman constant and T is the absolute temperature of the
surface in Kelvin. This equation is Stefan-Boltzman law.

5. 
b
E )

If we can plot monochromatic emissive power ( ) vs wavelength ( at different temperature as shown in Fig.
(Area under the curve at that temperature)



 
0
d
E
E b
b
Therefore at a particular temperature,

 d
E
dE b
b  b
dE 

 d

to
(if is the change of total emissive power for wavelengths ranging from )


d
dE
E b
b  Which is called spectral or radiation intensity of a black body. The figure shows that area
increases with temperature ie emissive power increases with temperature.

6. 


Emissivity( ) : The emissivity of a surface is defined as the ratio of radiation emitted by the surface to the radiation emitted by a black body at
the same temperature.
Varies from 0 to 1, for black body =1,
)
(
)
(
)
(
T
E
T
E
t
b


4
T
E
E b 
 

Kirchhoffs law

7. A small body of surface area A1 is placed in a hollow
evacuated space kept at a constant uniform temperature T

*
1
1 E
A

1

Let the energy fall on the unit surface of the body at the rate E* of this
energy, generally a fraction
will be absorbed by a small body. Thus the
energy absorbed by the small body A1 is
,
=is the absorptivity of the small body
When thermal equilibrium (steady state) is attained.
Energy absorbed by the body =Energy emitted (error In
fig)
Energy absorbed by A1=
*
1
1 E
A 


E1=Energy emitted by A1 surface/area
At steady state, 1
1
*
1
1 A
E
E
A 




Similarly if we replace the body A1 by A2, Then 2
2
*
2
2 A
E
E
A 




















b
b
b
b
E
E
E
E
E
E
E
E
2
2
1
1
*
Kirchhoff’s law also states that the
emissivity of a body is equal to its
absorptivity when the body remains
in thermal equilibrium with its
surroundings.
The law states that at any
temperature the ratio of total
emissive power E to the total
absorptivity is constants for all
substances which are in thermal

8. Planck’s law
  1
5
2
exp
2









KT
Ch
h
C
E b




 
K
re,
temperatu
Abs
T
J/K
10
1.380
constant
Boltzman
K
μm
,
Wavelength
λ
Js
10
6.625
constant
Planks
h
m/s
10
3
in vacuum
light
of
Velocity
C
)
(W/m
body
black
a
of
power
emmisive
tic
Monochroma
E
23
-
34
8
2
b
λ













  1
2
5
1
exp
as
written
is
law
Planks
often the
Quite









KT
C
C
E b


 



0
b
E
power,
emmisive
Total 
 d
Eb
max
 constant.
.
max 
T


Wein’s displacement law: It states that the product of and T is constant, i.e.,
The maximum values of the emissive power Eb can
be obtained by differentiating
Planck’s Equation wrt and equating it to zero, therefore,
   
        
   
 
mK
T
T
C
x
x
e
x
e
e
C
T
C
T
e
e
e
T
C
e
C
e
e
T
C
e
C
e
C
d
d
d
E
d
x
x
x
T
C
T
C
T
C
T
C
T
C
T
C
T
C
T
C
b
3
max
max
2
2
2
2
1
/
/
1
/
2
2
1
/
6
1
1
/
/
2
2
2
/
5
1
1
/
5
1
10
898
.
2
965
.
4
0
1
5
5
1
5
5
1
5
/
1
0
5
.
1
/
1
1
0
1
2
2
2
2
2
2
2
2














































 























