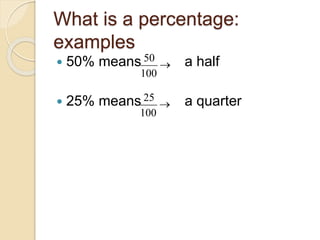This document discusses percentages and percent problems. It defines a percentage as a fraction with a denominator of 100. Percentages make it easy to compare quantities. A percent problem has three parts: the amount, the base, and the percent. The amount is part of the whole (base). The percent expresses the ratio of the amount to the base as a percentage. The document provides examples and exercises for identifying these parts and calculating unknown values in percent problems using the formula: Percent = Amount/Base x 100.

1. Percentages

2. Learning objectives
 Describe the meaning of percentage
 Identify the amount in a percent
problem
 Identify the base in a percent problem
 Identify the percent in a percent
problem
 Find the unknown quantity (amount,
base or percent) in a percent problem

3. What is a percentage
 A percentage is the top part of a
fraction whose bottom part is 100.
 Percentages are useful because they
make it very easy to compare things.

4. What is a percentage:
examples
 50% means a half
 25% means a quarter
50
100
®
25
100
®

5. What is a percentage:
examples
 Percentages are useful because they
make it very easy to compare things:
I got different marks in two exams: I got
24/30 in the first exam and 36/60 in the
second one. How can I compare these
marks? I can change in some way the
maximum mark to 100 for both the exams:
Now I can compare the marks.
24
30
=
80
100
and
36
60
=
60
100

6. The three parts of a percent
problem
 The base is the whole in a percent
problem
 The amount is a part of the whole
 The percent (or rate) is the ratio of the
amount to the base, written as a
percent

7. The three parts of a percent
problem
 Calculate the 20% of 800:
So 160 is the 20% of 800
In this example 160 is the amount, 800 is
the base and 20 is the percent.
800
100
×20 =160

8. Exercise
 Identify base, amount and percent in
the following examples:
21 is the 70% of 30
36 is the 60% of 60
Amount Base Percent

9. How to calculate
percent =
amount
base
100
base =
amount
percent
100
amount =
percent × base
100

10. Examples
 Calculate the 20% of 300
 The percent is 20%, the amount is 30,
calculate the base:
300
100
20 = 60
base =
30
20
100 =150

11. Examples
 The amount is 15, the base is 60,
calculate the percent
percent =
15
60
100 = 25%

12. Exercise
 Complete the table
Amount Base Percent
30 90
80 15
25 40