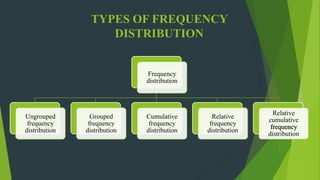
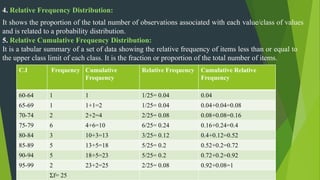
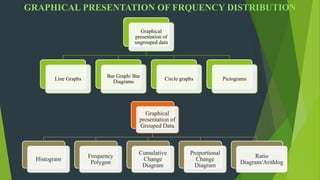
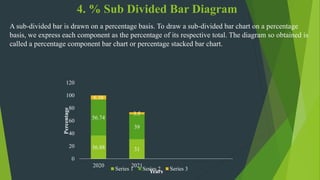
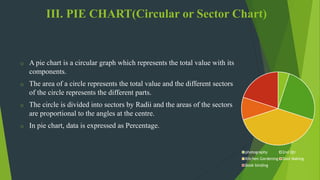
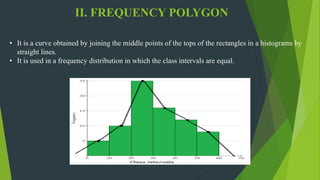
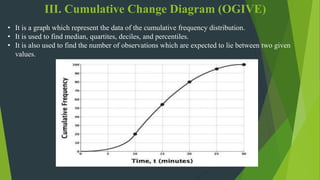
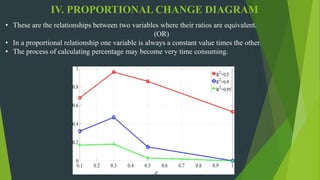
The document discusses frequency distribution in biostatistics, outlining its significance in summarizing observations across various classes or categories. It details different types of frequency distributions including ungrouped, grouped, cumulative, relative, and relative cumulative, along with examples and graphical representations such as histograms, bar diagrams, and pie charts. Additionally, the document explains how to visually present data through methods like line graphs and pictograms.

1. BIOSTATISTICS AND RESEARCH METHODOLOGY
Unit-1: frequency distribution
PRESENTED BY
Himanshu Rasyara
B. Pharmacy IV Year
UNDER THE GUIDANCE OF
Gangu Sreelatha M.Pharm., (Ph.D)
Assistant Professor
CMR College of Pharmacy, Hyderabad.
email: sreelatha1801@gmail.com

2. FREQUENCY DISTRIBUTION
• When observations, discrete or continuous are available on a single characteristic of
a large number of individuals, often it becomes necessary to condense the data as
far as possible without losing any information of interest.
• The frequency distribution is an example of such a data summary, a
table/categorisation of the frequency of occurrence of variables in various class
intervals.
• Sometimes a frequency distribution of a set of data is simply called a
“Distribution”.
• For a sampling of continuous data, in general a frequency distribution is constructed
by classifying the observations (variables) into a number of discrete intervals.
• For categorial data, frequency distribution is simply a listing of number of
observations in each class or category, such as 20 males and 30 females entered in a
clinical study.
• A frequency distribution can be graphed as a histogram or pie chart.

3. TYPES OF FREQUENCY
DISTRIBUTION
Frequency
distribution
Ungrouped
frequency
distribution
Grouped
frequency
distribution
Cumulative
frequency
distribution
Relative
frequency
distribution
Relative
cumulative
frequency
distribution

4. 1. Ungrouped Frequency Distribution:
o Used for discrete variables.
o Also called “RAW DATA”.
o Includes data that has not been organised into
groups like gender, martial status, types of family.
DATA FREQUENCY
2 8
3 4
5 6
7 7
8 2
9 5
2. Grouped Frequency Distribution:
o They have class intervals.
o It includes data that has been organised into groups(into a frequency
distribution)
o It is used if variables are continuous such as age, salary, body temperature, etc.
DATA FREQUENCY
2-4 5
5-7 6
8-10 10
11-13 8
14-16 4
17-19 3
3. Cumulative Frequency Distribution:
o These are used to determine the number of observations that lie above/below a particular value in a
data set.
o It also helps us to observe and understand how the values within a particular data set changes.

5. 4. Relative Frequency Distribution:
It shows the proportion of the total number of observations associated with each value/class of values
and is related to a probability distribution.
5. Relative Cumulative Frequency Distribution:
It is a tabular summary of a set of data showing the relative frequency of items less than or equal to
the upper class limit of each class. It is the fraction or proportion of the total number of items.
C.I Frequency Cumulative
Frequency
Relative Frequency Cumulative Relative
Frequency
60-64 1 1 1/25= 0.04 0.04
65-69 1 1+1=2 1/25= 0.04 0.04+0.04=0.08
70-74 2 2+2=4 2/25= 0.08 0.08+0.08=0.16
75-79 6 4+6=10 6/25= 0.24 0.16+0.24=0.4
80-84 3 10+3=13 3/25= 0.12 0.4+0.12=0.52
85-89 5 13+5=18 5/25= 0.2 0.52+0.2=0.72
90-94 5 18+5=23 5/25= 0.2 0.72+0.2=0.92
95-99 2 23+2=25 2/25= 0.08 0.92+0.08=1
Σf= 25

6. GRAPHICAL PRESENTATION OF FRQUENCY DISTRIBUTION
Graphical
presentation of
Grouped Data
Histogram
Frequency
Polygon
Cumulative
Change
Diagram
Proportional
Change
Diagram
Ratio
Diagram/Arithlog
Graphical
presentation of
ungrouped data
Line Graphs
Bar Graph/ Bar
Diagrams
Circle graphs Pictograms

7. I. LINE GRAPHS
102
104
106
108
110
112
Column2 Series 2 Column1
• Line graphs are simple mathematical graphs that are drawn on the graph paper by plotting the data
concerning one variable on the horizontal x- axis and other variable of data on the vertical y- axis.

8. II. BAR DIAGRAM
o Used for comparison of Quantitative data.
% Subdivided Bar
Diagram Simple Bar Diagram
Subdivided/Component
Bar Diagram
Multiple /Grouped Bar
Diagram
Bar Diagram
Types of Bar diagram

9. 1. Simple Bar Diagram
30
35
25
45
10
40
0
5
10
15
20
25
30
35
40
45
50
%
of
patients
with
given
response
Response
• It is used to compare two or more items related to a
variable.
• The data is presented with the help of bars.
• The length of bar is determine by the value or amount of
variables.
• A limitation of simple bar diagram is that only one
variable can be represented on it.

10. 2. Multiple/Grouped Bar Diagram
42
40
20
25
35
45
0 5 10 15 20 25 30 35 40 45 50
Poor
Fair
Good
% of patients in Category
• It is use when a number of items are to be compared in respect of two, three or more values.
• In this case the numerical values of major categories are arranged in ascending or descending order so
that the categories can be readily distinguished.
• Different shades/colours are used for each categories.

11. 3. Sub Divided/Component Bar Diagram
0
100
200
300
400
500
600
700
800
900
X Y Z
People’s
response/Side
effects
Drugs
• It is formed by dividing a single bar into several component parts. A single bar represents the
aggregate value whereas the component parts represent the component values of the aggregate
value.

12. 4. % Sub Divided Bar Diagram
36.88 31
56.74
39
6.38
3.5
0
20
40
60
80
100
120
2020 2021
Percentage
Years
Series 1 Series 2 Series 3
A sub-divided bar is drawn on a percentage basis. To draw a sub-divided bar chart on a percentage
basis, we express each component as the percentage of its respective total. The diagram so obtained is
called a percentage component bar chart or percentage stacked bar chart.

13. III. PIE CHART(Circular or Sector Chart)
o A pie chart is a circular graph which represents the total value with its
components.
o The area of a circle represents the total value and the different sectors
of the circle represents the different parts.
o The circle is divided into sectors by Radii and the areas of the sectors
are proportional to the angles at the centre.
o In pie chart, data is expressed as Percentage.
photography 2nd Qtr
Kitchen Gardening Dool Making
Book binding

14. IV. PICTOGRAM
• It is a way of representing statistical data in pictures.
• In this a number of pictures of same size and equal in value are drawn. Each pictures represents a
number of units.
• The chief advantage of this method is it presents data in a very attractive way.

15. I. HISTOGRAM
o A histogram is a graph containing a set of rectangles, each being constructed to represent the size of
the class interval by its width and the frequency in each class interval by its height.

16. II. FREQUENCY POLYGON
• It is a curve obtained by joining the middle points of the tops of the rectangles in a histograms by
straight lines.
• It is used in a frequency distribution in which the class intervals are equal.

17. III. Cumulative Change Diagram (OGIVE)
• It is a graph which represent the data of the cumulative frequency distribution.
• It is used to find median, quartites, deciles, and percentiles.
• It is also used to find the number of observations which are expected to lie between two given
values.

18. IV. PROPORTIONAL CHANGE DIAGRAM
• These are the relationships between two variables where their ratios are equivalent.
(OR)
• In a proportional relationship one variable is always a constant value times the other.
• The process of calculating percentage may become very time consuming.

19. V. RATIO DIAGRAM
• This diagram has the added advantage that both relative and absolute changes can be determined
from it.
• The bases of the construction is the use of a special paper known as “Arithlog or Ratio Paper”. It
is provided in various sizes.
• It can not be easily understood by an untrained person.