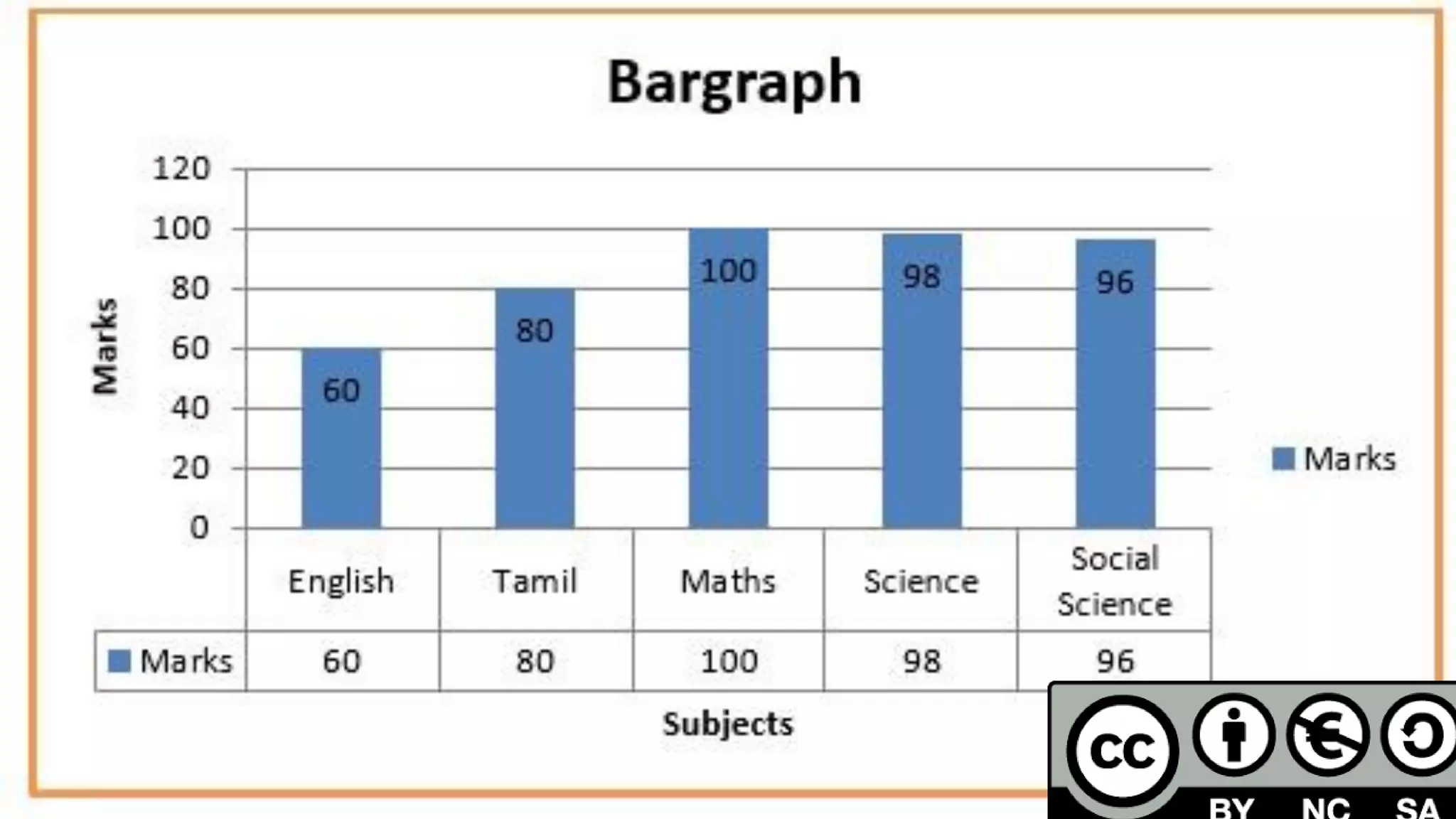
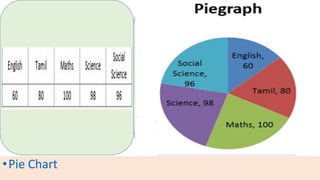
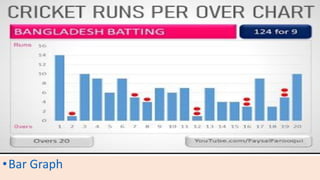
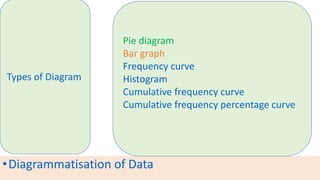
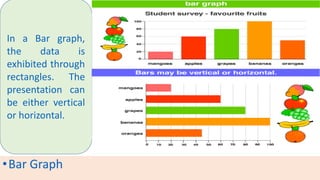
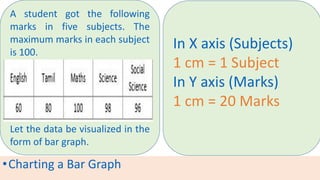
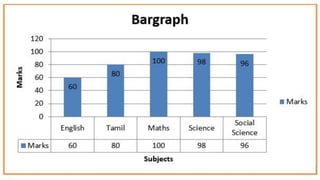
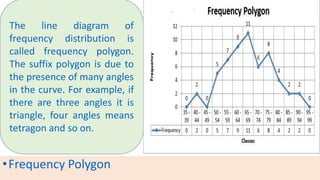
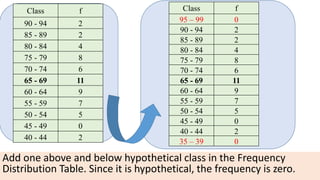
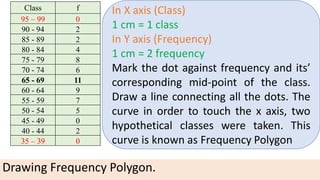
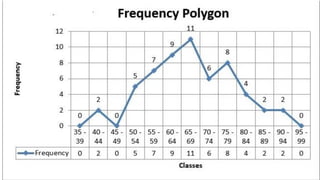
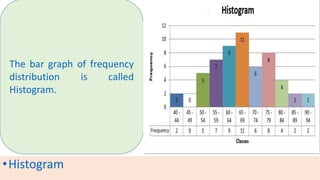
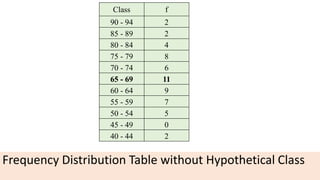
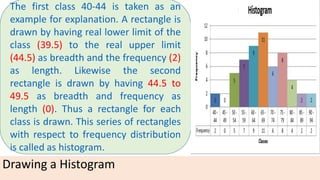
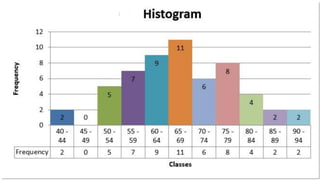
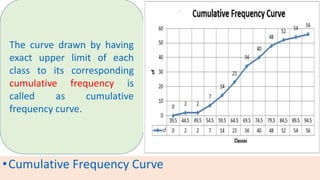
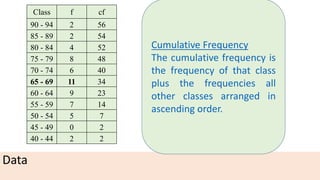
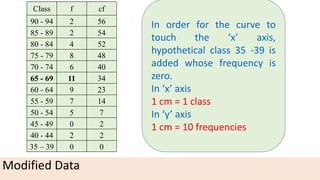
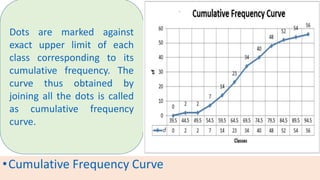
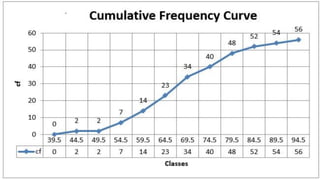
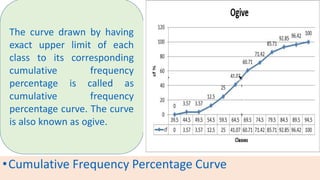
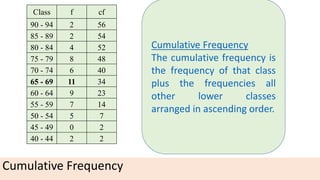
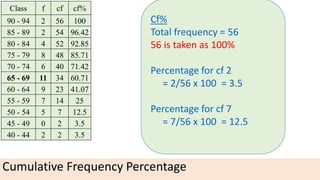
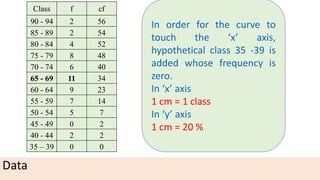
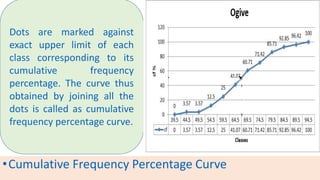
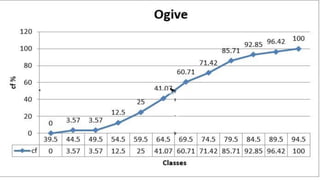
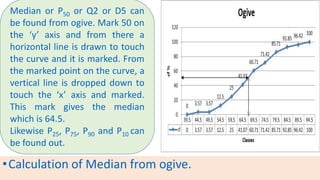
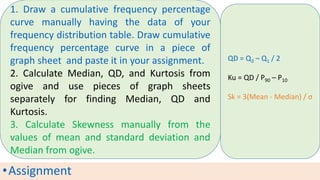
The document provides information about different types of diagrams used to represent statistical data visually, including pie charts, bar graphs, frequency polygons, histograms, and cumulative frequency curves. It explains how to construct each type of diagram by plotting variables like frequency and class on x and y axes. Examples are given of drawing each diagram based on sample data. The document also discusses concepts like percentiles, quartiles, and deciles for dividing a data set and calculating measures like median and skewness from a cumulative frequency curve.

2. •Diagramming the Data
Picture can speak 1000
words. Rather than
telling about whole
drama of a 20/20 cricket
match, just the picture
on the right, is enough.
Statistics also gives data
in the form of diagram
and it is more elegant to
see.

3. •Diagrammatisation of Data
Types of Diagram
Pie diagram
Bar graph
Frequency Polygon
Histogram
Cumulative frequency curve
Cumulative frequency percentage curve

4. •Pie Diagram
Pie diagram is in the form of circle,
hence it is also called as circle
diagram. It can be fragmented in to
different proportions, which
represents the data.
In English, the word pie means a type
of food made with meat, vegetables
or fruit covered in pastry and baked.

5. •Charting a Pie
A student got the
following marks in five
subjects. The maximum
marks in each subject is
100.
Let the data be visualized
in the pie form.
Total angle in a pie = 3600
Total marks for all subjects = 434/500
For English
For 434 marks = 3600
for 60 marks=60x360/434 = 49.70≈500
Like above Tamil = 66.60≈670
Maths = 82.90≈830
Science=81.20≈810
Social Science = 79.60≈800

6. •Pie Chart
isualized in the pie form.

7. •Assignment
Draw a pie chart manually having your own X standard marks.

8. •Bar Graph

9. •Diagrammatisation of Data
Types of Diagram
Pie diagram
Bar graph
Frequency curve
Histogram
Cumulative frequency curve
Cumulative frequency percentage curve

10. •Bar Graph
In a Bar graph,
the data is
exhibited through
rectangles. The
presentation can
be either vertical
or horizontal.

11. •Charting a Bar Graph
A student got the following
marks in five subjects. The
maximum marks in each subject
is 100.
Let the data be visualized in the
form of bar graph.
In X axis (Subjects)
1 cm = 1 Subject
In Y axis (Marks)
1 cm = 20 Marks

13. •Assignment
Draw a Bar Graph manually having your own X standard marks. Draw
in a piece of graph sheet and paste it in your assignment.

14. •Frequency Polygon
Types of Diagram
Pie diagram
Bar graph
Frequency Polygon
Histogram
Cumulative frequency curve
Cumulative frequency percentage curve

15. •Frequency Polygon
The line diagram of
frequency distribution is
called frequency polygon.
The suffix polygon is due to
the presence of many angles
in the curve. For example, if
there are three angles it is
triangle, four angles means
tetragon and so on.

16. Add one above and below hypothetical class in the Frequency
Distribution Table. Since it is hypothetical, the frequency is zero.
Class f
90 - 94 2
85 - 89 2
80 - 84 4
75 - 79 8
70 - 74 6
65 - 69 11
60 - 64 9
55 - 59 7
50 - 54 5
45 - 49 0
40 - 44 2
Class f
95 – 99 0
90 - 94 2
85 - 89 2
80 - 84 4
75 - 79 8
70 - 74 6
65 - 69 11
60 - 64 9
55 - 59 7
50 - 54 5
45 - 49 0
40 - 44 2
35 – 39 0

17. Drawing Frequency Polygon.
In X axis (Class)
1 cm = 1 class
In Y axis (Frequency)
1 cm = 2 frequency
Mark the dot against frequency and its’
corresponding mid-point of the class.
Draw a line connecting all the dots. The
curve in order to touch the x axis, two
hypothetical classes were taken. This
curve is known as Frequency Polygon
Class f
95 – 99 0
90 - 94 2
85 - 89 2
80 - 84 4
75 - 79 8
70 - 74 6
65 - 69 11
60 - 64 9
55 - 59 7
50 - 54 5
45 - 49 0
40 - 44 2
35 – 39 0

19. •Assignment
Draw a frequency polygon manually having the data of your
frequency distribution table drawn before. Draw frequency polygon
in a piece of graph sheet and paste it in your assignment.

20. •Frequency Polygon
Types of Diagram
Pie diagram
Bar graph
Frequency Polygon
Histogram
Cumulative frequency curve
Cumulative frequency percentage curve

21. •Histogram
The bar graph of frequency
distribution is called
Histogram.

22. Frequency Distribution Table without Hypothetical Class
Class f
90 - 94 2
85 - 89 2
80 - 84 4
75 - 79 8
70 - 74 6
65 - 69 11
60 - 64 9
55 - 59 7
50 - 54 5
45 - 49 0
40 - 44 2

23. Drawing a Histogram
In X axis (Class)
1 cm = 1 class
In Y axis (Frequency)
1 cm = 2 frequency
Class f
90 - 94 2
85 - 89 2
80 - 84 4
75 - 79 8
70 - 74 6
65 - 69 11
60 - 64 9
55 - 59 7
50 - 54 5
45 - 49 0
40 - 44 2

24. Drawing a Histogram
The first class 40-44 is taken as an
example for explanation. A rectangle is
drawn by having real lower limit of the
class (39.5) to the real upper limit
(44.5) as breadth and the frequency (2)
as length. Likewise the second
rectangle is drawn by having 44.5 to
49.5 as breadth and frequency as
length (0). Thus a rectangle for each
class is drawn. This series of rectangles
with respect to frequency distribution
is called as histogram.

26. Drawing a Histogram
The base of each rectangle is same,
because
Base α i (class interval)
The length of the each rectangle is
different because
Length α f (frequency)
Area of Histogram α N (Total number of
scores)

27. •Assignment
Draw a histogram manually having the data of your frequency
distribution table drawn before. Draw Histogram in a piece of graph
sheet and paste it in your assignment.

28. •Frequency Polygon
Types of Diagram
Pie diagram
Bar graph
Frequency Polygon
Histogram
Cumulative frequency curve
Cumulative frequency percentage curve

29. •Cumulative Frequency Curve
The curve drawn by having
exact upper limit of each
class to its corresponding
cumulative frequency is
called as cumulative
frequency curve.

30. Data
Class f cf
90 - 94 2 56
85 - 89 2 54
80 - 84 4 52
75 - 79 8 48
70 - 74 6 40
65 - 69 11 34
60 - 64 9 23
55 - 59 7 14
50 - 54 5 7
45 - 49 0 2
40 - 44 2 2
Cumulative Frequency
The cumulative frequency is
the frequency of that class
plus the frequencies all
other classes arranged in
ascending order.

31. Modified Data
Class f cf
90 - 94 2 56
85 - 89 2 54
80 - 84 4 52
75 - 79 8 48
70 - 74 6 40
65 - 69 11 34
60 - 64 9 23
55 - 59 7 14
50 - 54 5 7
45 - 49 0 2
40 - 44 2 2
35 – 39 0 0
In order for the curve to
touch the ‘x’ axis,
hypothetical class 35 -39 is
added whose frequency is
zero.
In ‘x’ axis
1 cm = 1 class
In ‘y’ axis
1 cm = 10 frequencies

32. •Cumulative Frequency Curve
Dots are marked against
exact upper limit of each
class corresponding to its
cumulative frequency. The
curve thus obtained by
joining all the dots is called
as cumulative frequency
curve.

34. •Assignment
Draw a cumulative frequency curve manually having the data of your
frequency distribution table. Draw cumulative frequency curve in a
piece of graph sheet and paste it in your assignment.

35. •Cumulative Frequency Percentage Curve
Types of Diagram
Pie diagram
Bar graph
Frequency Polygon
Histogram
Cumulative frequency curve
Cumulative frequency percentage curve

36. •Cumulative Frequency Percentage Curve
The curve drawn by having
exact upper limit of each
class to its corresponding
cumulative frequency
percentage is called as
cumulative frequency
percentage curve. The curve
is also known as ogive.

37. Cumulative Frequency
Class f cf
90 - 94 2 56
85 - 89 2 54
80 - 84 4 52
75 - 79 8 48
70 - 74 6 40
65 - 69 11 34
60 - 64 9 23
55 - 59 7 14
50 - 54 5 7
45 - 49 0 2
40 - 44 2 2
Cumulative Frequency
The cumulative frequency is
the frequency of that class
plus the frequencies all
other lower classes
arranged in ascending order.

38. Cumulative Frequency Percentage
Class f cf cf%
90 - 94 2 56 100
85 - 89 2 54 96.42
80 - 84 4 52 92.85
75 - 79 8 48 85.71
70 - 74 6 40 71.42
65 - 69 11 34 60.71
60 - 64 9 23 41.07
55 - 59 7 14 25
50 - 54 5 7 12.5
45 - 49 0 2 3.5
40 - 44 2 2 3.5
Cf%
Total frequency = 56
56 is taken as 100%
Percentage for cf 2
= 2/56 x 100 = 3.5
Percentage for cf 7
= 7/56 x 100 = 12.5

39. Data
Class f cf
90 - 94 2 56
85 - 89 2 54
80 - 84 4 52
75 - 79 8 48
70 - 74 6 40
65 - 69 11 34
60 - 64 9 23
55 - 59 7 14
50 - 54 5 7
45 - 49 0 2
40 - 44 2 2
35 – 39 0 0
In order for the curve to
touch the ‘x’ axis,
hypothetical class 35 -39 is
added whose frequency is
zero.
In ‘x’ axis
1 cm = 1 class
In ‘y’ axis
1 cm = 20 %

40. •Cumulative Frequency Percentage Curve
Dots are marked against
exact upper limit of each
class corresponding to its
cumulative frequency
percentage. The curve thus
obtained by joining all the
dots is called as cumulative
frequency percentage curve.

42. •Percentile - Concept
Percentile is a point in the data line below which given percentage of
score lies. Let all the scores be divided into 100 equal parts. It is
called as percentiles and can be represented as follows;

43. •Percentile - Concept
The 1st percentile is a point below which 1% of score lies and above which
99% of score lies. It is represented as P1. Going further P20 is a point below
which 20% of score lies and above which 80% of score lies.
What about P50?
P50 is a point below and above which 50% of score lies. This point is
otherwise known as Median.

44. •Quartile - Concept
The data line can be divided into four quadrants. Each quadrant is
termed as quartile. Q1 is first quartile and Q2 is second quartile and
so on. Q2 is Median.
This can be diagrammatically represented in data line as

45. •Decile - Concept
The data line can be divided into 10 equal parts. Each point is termed
as a Decile. Q1 is first quartile and Q2 is second quartile and so on. Q2
is Median.
This can be diagrammatically represented in data line as

46. •Percentile – Quartile - Decile

47. •Calculation of Median from ogive.
Median or P50 or Q2 or D5 can
be found from ogive. Mark 50 on
the ‘y’ axis and from there a
horizontal line is drawn to touch
the curve and it is marked. From
the marked point on the curve, a
vertical line is dropped down to
touch the ‘x’ axis and marked.
This mark gives the median
which is 64.5.
Likewise P25, P75, P90 and P10 can
be found out.

48. •Assignment
1. Draw a cumulative frequency percentage
curve manually having the data of your
frequency distribution table. Draw cumulative
frequency percentage curve in a piece of
graph sheet and paste it in your assignment.
2. Calculate Median, QD, and Kurtosis from
ogive and use pieces of graph sheets
separately for finding Median, QD and
Kurtosis.
3. Calculate Skewness manually from the
values of mean and standard deviation and
Median from ogive.
QD = Q3 – Q1 / 2
Ku = QD / P90 – P10
Sk = 3(Mean - Median) / σ

49. •Musings
With this, our class for this semester comes to an end. This is an
opportunity provided by you upon me. Thanks for coming along with
me in this journey. I can’t say that syllabus is covered but it has to be
discovered by us. Having said to take on Writing Questions,
Standardizing a Question Paper and Statistics, I have done a bit.

50. •Musings
The success of the teaching lies in applying all that you have learnt in
AL in understanding about measurement, assessment and
evaluation, different types of evaluation, writing GIO & SIO with
respect to Bloom’s taxonomy, writing questions, preparing blue print,
standardizing a question paper, fair evaluation of the scripts,
understand what the data says, ……

51. References
• Garrett, H. E. (1926). Statistics in psychology and education. Longman’s Green & Co
• Mathew, T.K., and Mollykutty, T.M. (2011). Science education -Theoretical bases of
teaching and pedagogic analysis - Physical Science and Natural Science. Rainbow Book
Publishers
• Mangal. S. K. (2014). Statistics in psychology and education. PHI Learning Private
Limited
• NCERT. (2013). Teaching of science.
• Radha Mohan. (2007). Teaching of physical science. (3rd ed.). PHI Learning
• Rathinasabapathy, P. (2001). கல்வியில் தேர்வு [Examination in Education]. (2nd
ed.). Shantha Publishers.
• Srinivasan, P. (2011). அறிவியல் கற்பிே்ேல் [Teaching of science]. DDE, Tamil
Univeristy
• Images from google