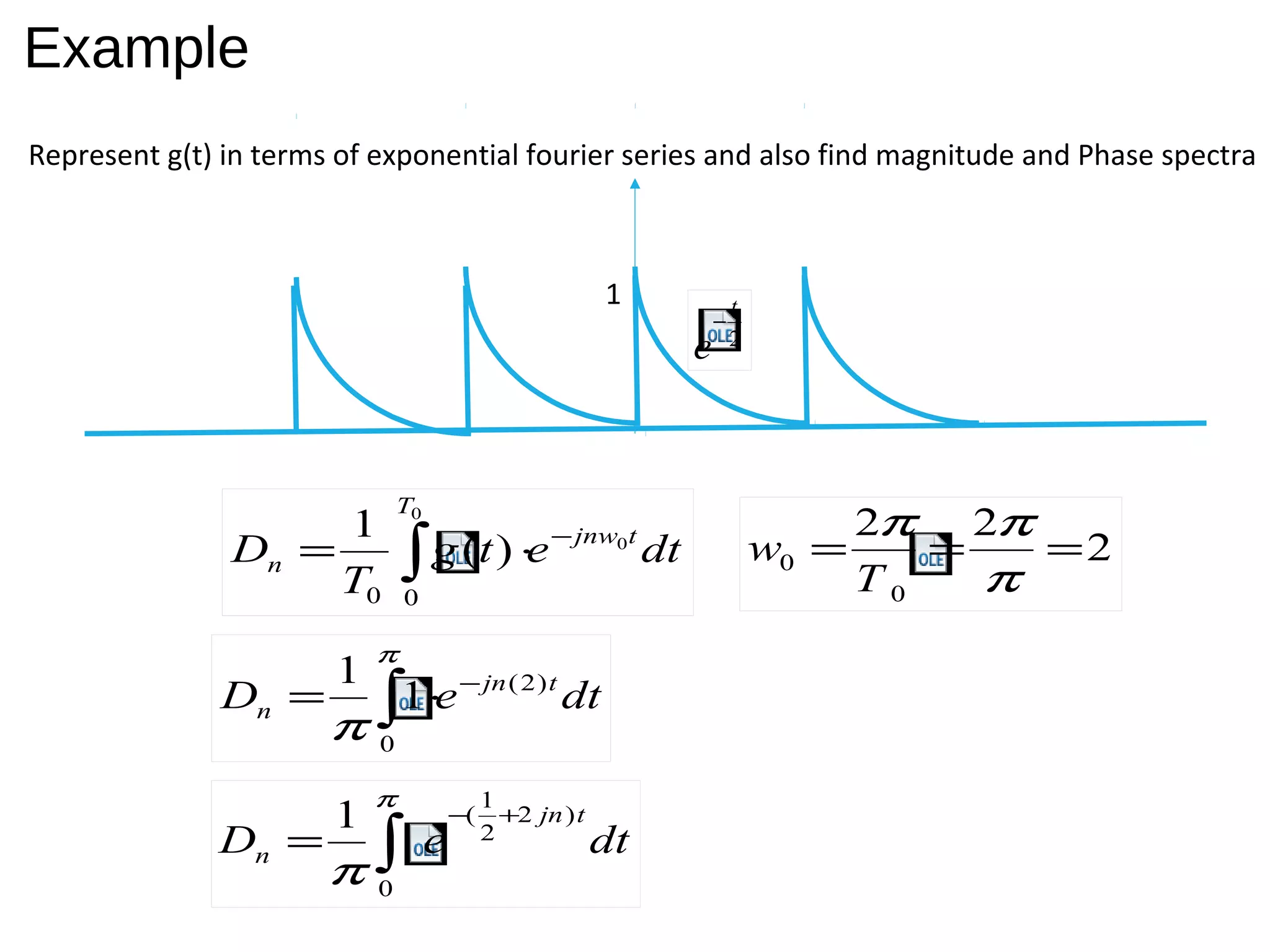
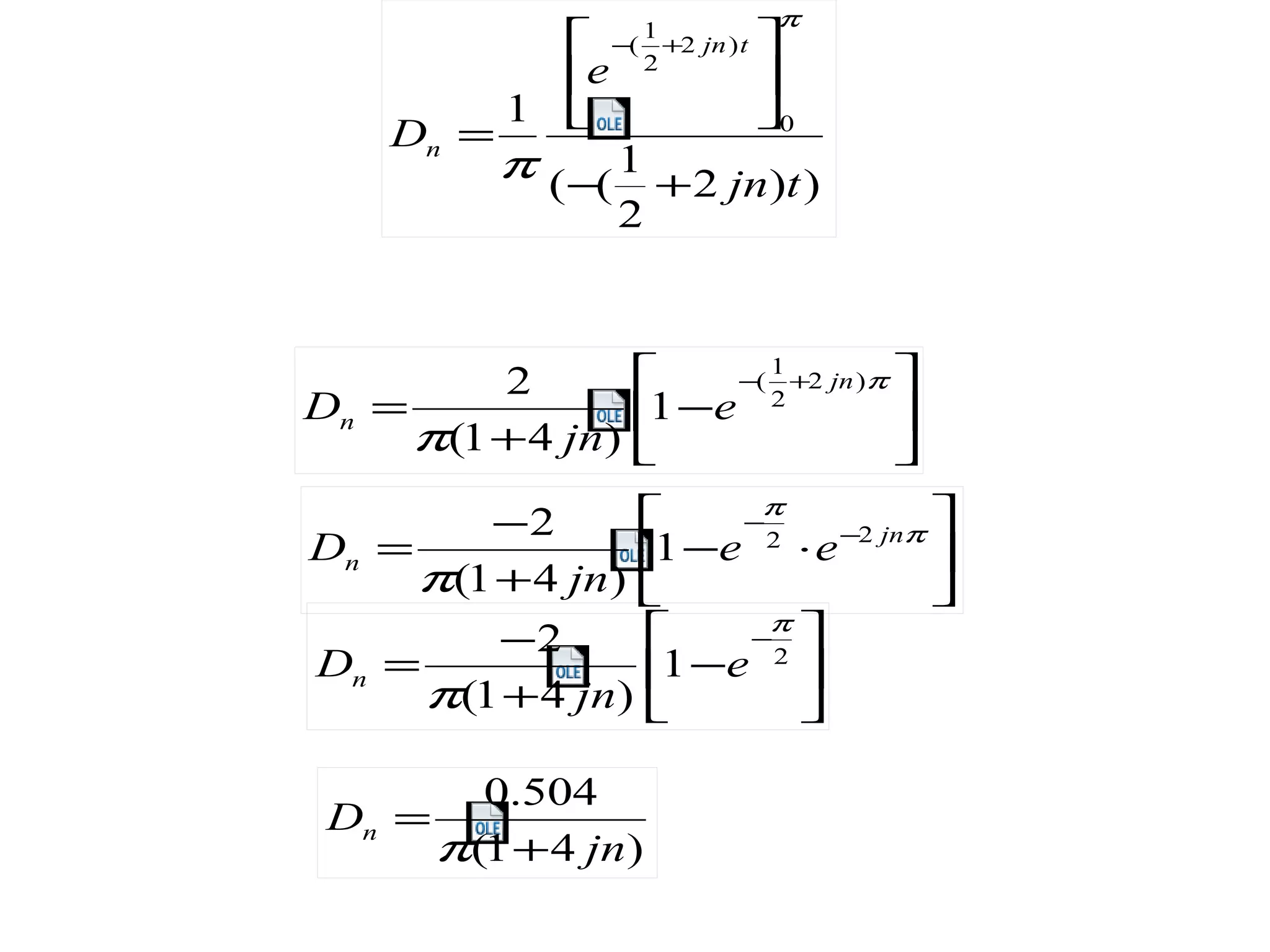
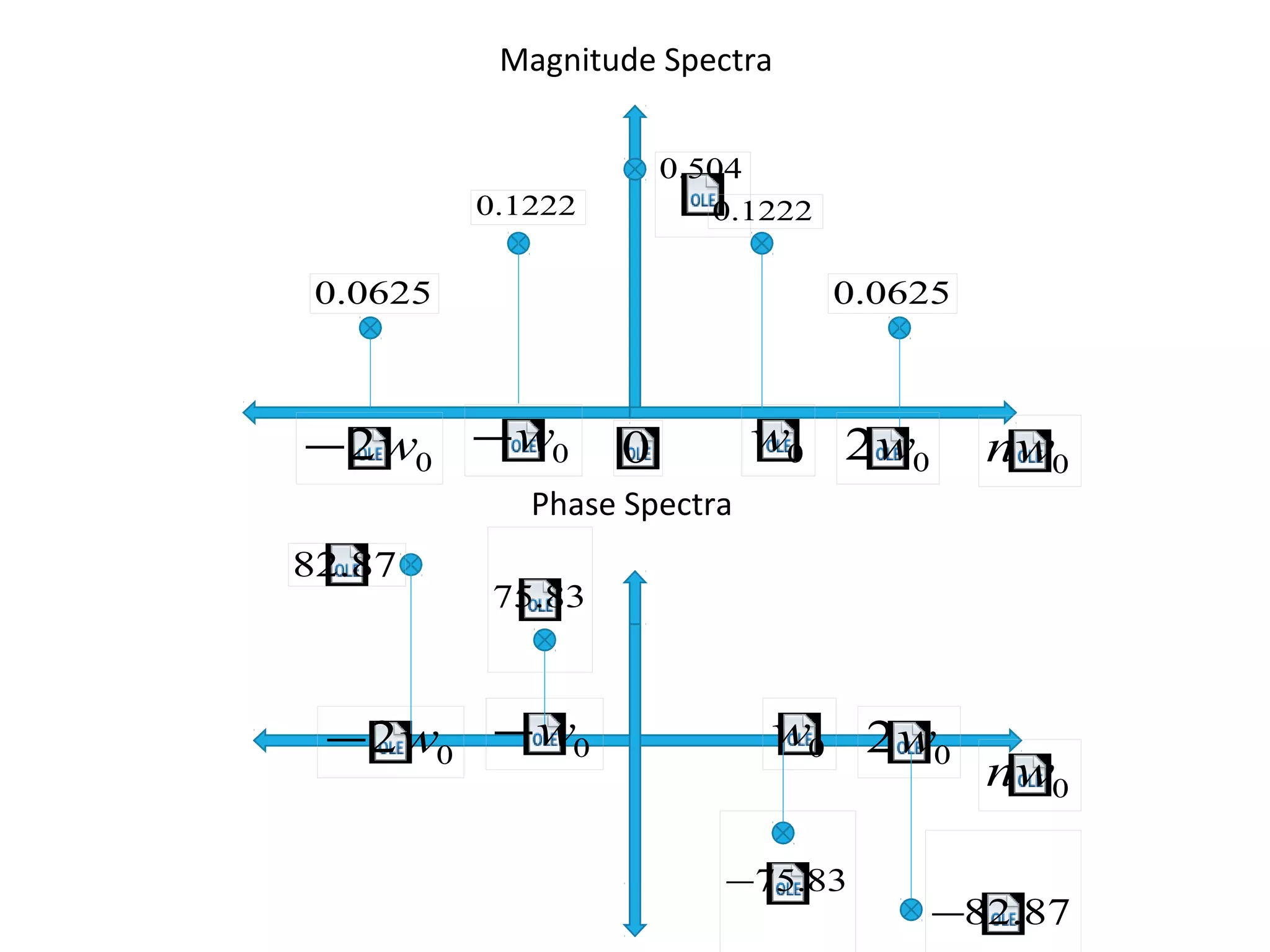
This document discusses Fourier series representation of signals. It defines orthogonal sets and explains that any signal can be represented as a combination of orthogonal basis functions using Fourier series. There are two common ways to represent a signal using Fourier series: using trigonometric or exponential basis functions. An example signal is represented using both trigonometric and exponential Fourier series. The magnitude and phase spectra of the example signal are also calculated from the Fourier series coefficients.

1. Prepared By:
Preet Aghera 140110111002
Denish Thummar 140110111061
G H Patel College of Engineering and
Technology - V V Nagar
Electronics and Communication
(2151004)
Guided By:Prof. Samir D. Trapasiya

2. Fourier Series Representation

3. /*Complete Set of orthogonal may create any signal from it.*/
,
condition for
orthogonal :
then two signal , are orthogonal.
)(1 tg )(2 tg
0)()( 2
0
1 =•∫
∞
tgtg
)(1 tg )(2 tg

4. Two way to Represent :
• Trigonometric Exponential
fourier series fourier series
Cos + Sin θj
e

5. Orthogonal
sets
Trigonomatric Fourier Sereis
0)()( 2
0
1 =•∫
∞
tgtg
0)()( 2
0
1
0
=•∫ tgtg
T
nmattmwtnw
T
≠=•∫ ,0)cos()cos( 0
0
0
0
nmT
== ,2
0
)3sin(),2sin(),sin(),0sin(
)3cos(),2cos(),cos(),0cos(
000
000
twtwtw
twtwtw

6. Fourier series
)]sin()cos([)( 00
1
0 tnwbtnwaatg nn ++= ∑
∞
∫
∫
∫
=
=
=
0
0
0
0
0
0
0
0
0
0
0
0
0
)sin()(
2
)cos()(
12
1
T
n
T
n
T
dttnwtg
T
b
dttnwtg
T
a
dta
T
a
where

7. Example
1
g(t)
QUE:Represent g(t) in Trigonomatric fourier series and also find magnitude and phase spectra
∫=
0
0
0
0
0
1
T
dta
T
a
2
π
2
π
−
ππ−
1
2
2
,2)(, 00 ===−−=
π
π
πππ wTPeriod
∫
−
=
2
2
2
1
π
ππ
dt 2
1
=

8. ∫=
0
0
0
0
)cos()(
2
T
n dttnwtg
T
a
∫
−
⋅=
2
2
)cos(1
)2(
2
π
ππ
dtntan
)
2
sin(
2sin1 2
2
π
ππ
π
π
n
nn
nt
an =





=
−
,...15,11,7,3,
2
,....13,9,5,1,
2
,...6,4,2,0
=−=
==
==
ifn
n
a
ifn
n
a
ifna
n
n
n
π
π

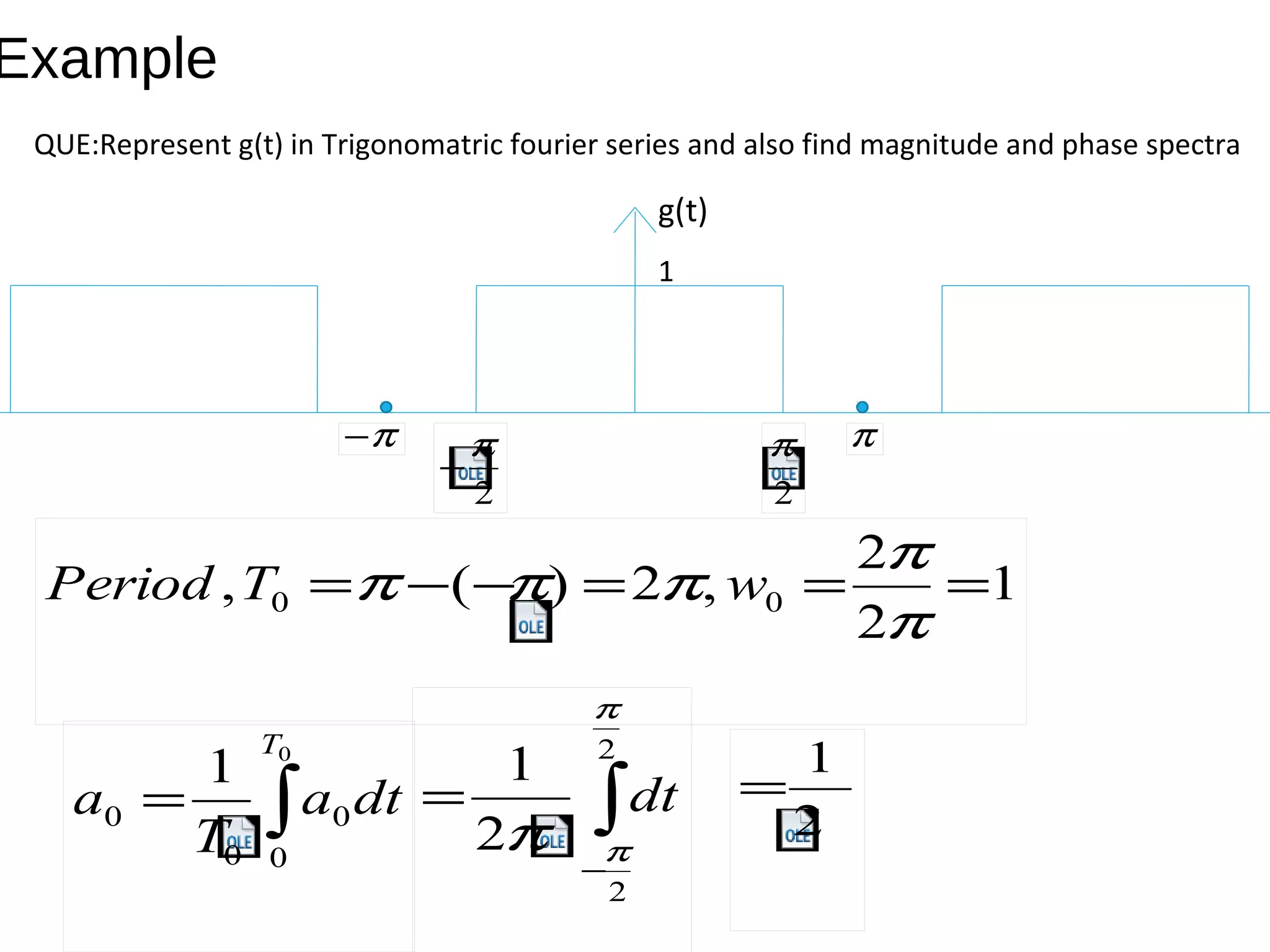
9. Fourier Series
Magnitude Spectra Phase Spectra
Magnitude
Freuency
Phase
Freuency
)]sin()cos([)( 00
1
0 tnwbtnwaatg nn ++= ∑
∞
)]cos()
2
sin(
2
[
2
1
)( 0
1
tnw
n
n
tg
n
⋅+= ∑
∞
=
π
π
...])5cos(
5
1
)3cos(
3
1
)[cos(
2
2
1
)( 000 ++−+= twtwtwtg
π

10. By putting value if an and bn in g(t)
na
nb nc
nθ
22
nnn bac +=
n
n
n
c
a
=θcos
n
n
n
c
b
=θsin
nnn ca θcos=
nnn cb θsin=
)]sin(sin)cos(cos[)( 00
1
0 tnwctnwcatg nnnn θθ ++= ∑
∞
)]cos([)( 0
1
0 n
n
n tnwcctg θ−+= ∑
∞
=
00 ac =

11. Magnitude Spectra Phase Spectra
May be zero…
nc
0nw0w 02w 03w 03w
0c
1c
2c
3c
nθ
0nw0w 02w 03w 03w
0θ
1θ
2θ
3θ
0c

12. Exponential Fourier Sereis
dtetg
T
D
where
eDtg
tjnw
T
n
tjnw
n
0
0
0
00
)(
1
)(
−
∞
∞−
∫
∑
⋅=
=
0
0
2
T
wwhere
π
==>

13. Example
Represent g(t) in terms of exponential fourier series and also find magnitude and Phase spectra
1
2
t
e
−
dtetg
T
D tjnw
T
n
0
0
00
)(
1 −
∫ ⋅= 2
22
0
0 ===
π
ππ
T
w
dteD tjn
n
)2(
0
1
1 −
∫ ⋅=
π
π
dteD
tjn
n
)2
2
1
(
0
1 +−
∫=
π
π

14. ))2
2
1
((
1 0
)2
2
1
(
tjn
e
D
tjn
n
+−






=
+−
π
π






−
+
=
+− π
π
)2
2
1
(
1
)41(
2 jn
n e
jn
D






⋅−
+
−
= −
−
π
π
π
jn
n ee
jn
D 22
1
)41(
2






−
+
−
=
−
2
1
)41(
2
π
π
e
jn
Dn
)41(
504.0
jn
Dn
+
=
π

15. Fourier series
,......2,1,0,1,2.....
)41(
504.0
)( 2
−−=
+
= ∑
∞
−∞=
n
e
jn
tg jnt
n π
tjnw
neDtg 0
)( ∑
∞
∞−
=
jtjt
jtjt
n
e
j
e
j
e
j
e
j
tg
42
24
)81(
504.0
)41(
504.0
504.0
)41(
504.0
)81(
504.0
)(
+
+
+
+
+
−
+
−
= −−
∞
−∞=
∑
ππ
ππ

16. )81(
504.0
2
j
D
−
=−
π
0625.0
65
504.0
)81(
504.0
2 ==
−
=−
j
D
π
)41(
504.0
1
j
D
−
=
π
87.82
1
8
tan 1
2 =





−=∠ −
−D
1222.0
17
504.0
)41(
504.0
1 ==
−
=−
j
D
π
83.75
1
4
tan 1
1 =





−=∠ −
−D
0,504.0 00 =∠= DD
83.75)4(tan,122.0 1
11 −==∠= −
DD
87.82,0625.0 22 −=∠= DD

17. Magnitude Spectra
Phase Spectra
0w 02w0w−02w−
0w 02w0w−02w−
0 0nw
0nw
504.0
1222.0
0625.0 0625.0
1222.0
87.82−
87.82
83.75−
83.75

18. THANK YOU