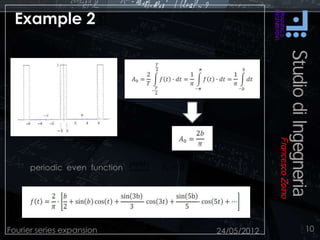
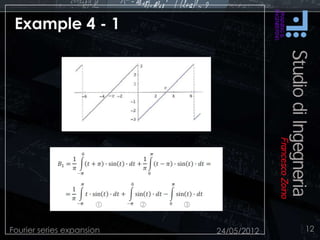
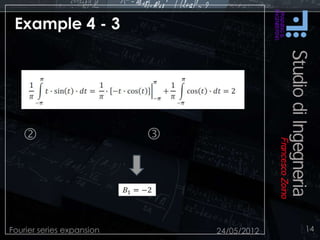
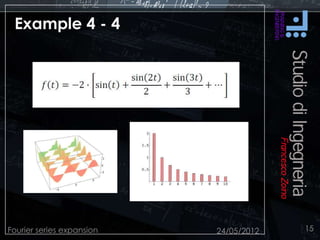
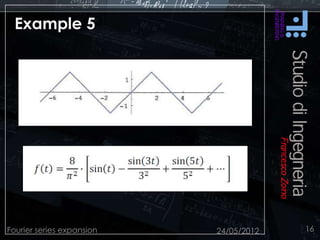
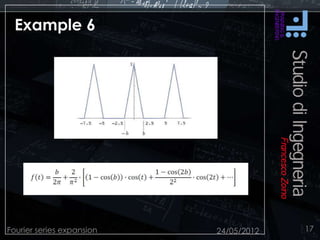
This document discusses Fourier series expansion and spectral analysis. It explains that while signals exist in the time domain, they can be represented in the frequency domain as a series of sinusoidal components at different frequencies. This frequency domain description is called spectral analysis. Spectral analysis of signals coupled with the frequency response of systems allows for better design work, as the behavior of a linear time-invariant system can be studied using sinusoidal signals. Fourier series expansion represents periodic functions as a series of sinusoidal functions, and was developed based on the work of French mathematician Jean Baptiste Joseph Fourier.

1. Fourier series expansion

2. Spectral analysis
Most part of signals involved in systems
working, are time-varying quantities.
Although a signal physically exists in
time domain, we can represent it in the
so called frequency domain, in which it
consists of a series of sinusoidal
components at various frequencies.
The frequency domain description is
called spectral analysis.
24/05/2012 2Fourier series expansion

3. LTI systems
The spectral analysis of signals, coupled with
frequency response characteristics of systems,
allows us to have a good approach in design
work.
In fact, when we can study the behavior of a
linear time-invariant (LTI) system in presence of
a particular sinusoidal signal, we can also
study the behavior in presence of all the
sinusoidal signals, and therefore in presence of
all the signals which we can consider
composed by a series of sinusoidal signals.
24/05/2012Fourier series expansion 3

4. Jean Baptiste Joseph Fourier
The mathematical methods
which help us in this work
are based on the studies of
a French physicist and
mathematician, Jean Bap-
tiste Joseph Fourier who
lived between XVIII and XIX
century.
24/05/2012Fourier series expansion 4

5. Methods
There are two kinds of methods:
• Series expansion of periodic signals
• Transform of non-periodic signals
24/05/2012Fourier series expansion 5

6. Series expansion
Every periodic function can be represented as
the expansion of a series of sinusoidal functions:
24/05/2012Fourier series expansion 6
where

7. Example 1 - 1
24/05/2012Fourier series expansion 7

8. Example 1 - 2
24/05/2012Fourier series expansion 8
periodic odd function

9. Example 1 - 3
24/05/2012Fourier series expansion 9
in the end:
If b=0, the function represents the restriction of function sgn(t)
into the ] interval, periodically extended outside. In the
figure below (left) are represented the first five Fourier
polynomials of this function.
The amplitude spectrum is a line spectrum (right figure).

10. Example 2
24/05/2012Fourier series expansion 10
periodic even function

11. Example 3
24/05/2012Fourier series expansion 11

12. Example 4 - 1
24/05/2012Fourier series expansion 12
  

13. Example 4 - 2
24/05/2012Fourier series expansion 13


14. Example 4 - 3
24/05/2012Fourier series expansion 14
 

15. Example 4 - 4
24/05/2012Fourier series expansion 15

16. Example 5
24/05/2012Fourier series expansion 16

17. Example 6
24/05/2012Fourier series expansion 17