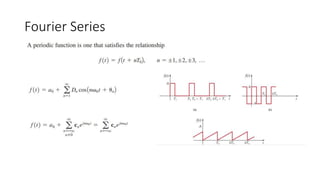
This document provides an overview of Fourier analysis techniques, including Fourier series and Fourier transforms, their applications in representing periodic and nonperiodic functions, and comparisons with Laplace transforms. It discusses key concepts such as trigonometric Fourier series, symmetry types, time shifting, and composite waveforms. The document emphasizes the mathematical formulation and utility of Fourier methods in waveform analysis.

1. Fourier Analysis Techniques
Part I

2. Contents
• Why Fourier Series and Fourier Transform?
• Fourier Series
• Exponential Fourier Series
• Derivation of Trigonometric Fourier Series
• Even, Odd and Half wave symmetry
• Time shifting
• Composite Waveform Generation
• Frequency Spectrum Construction

3. Usage of Fourier Series and Transform
• Fourier series is used to represent a periodic function by a discrete
sum of complex exponentials. The functions depends upon a
fundamental frequency and its harmonics.
• Fourier transform is then used to represent a general, nonperiodic
function by a continuous superposition or integral of complex
exponentials. The function is continuous w.r.t frequency and is
defined for every instant.
• The Fourier transform can be viewed as the limit of the Fourier series
of a function with the period approaches to infinity, so the limits of
integration change from one period to (−∞,∞).

4. Fourier vs Laplace
• Fourier series is not comparable with Laplace Transform
• Fourier Transform is comparable with Laplace Transform
• Laplace is used for real world signal where the signal starts at t=0 or t>0
• Laplace has both decaying/attenuating component and complex frequency
component, collectively called s.
• Fourier series and transforms, both has only complex frequency
component called omega (ꙍ). There is no sigma (σ) as in s= σ+jꙍ
• Fourier analysis is always done for a periodic signal
• if a signal is not periodic, we consider this to be periodic between (−∞,∞).
• If a signal is purely periodic with finite time period, we develop Fourier series for it
• If a signal is periodic having time period of infinity, we develop its transformed
version as Fourier Transform

5. Fourier Series

6. Derivation of Trigonometric FS from Exponential

7. Exponential Fourier Series

8. Trigonometric Fourier Series
f(t)

11. Even, Odd and Half wave symmetry

12. Even Symmetry

13. Odd Symmetry
Odd symmetric function must pass through origin besides other properties

14. Half wave symmetry

15. Example considering the odd, even and half wave symmetry discussion

16. Example considering the odd, even and half wave symmetry discussion

17. Example considering the odd, even and half wave symmetry discussion

18. Time shifting

19. Composite Waveform Generation
Fourier series and transforms both give us
mathematical formulation of a wave form and it
is piece wise additive as well.
This concludes that, while computing, we can use
the same equations to extrapolate our analysis as
well as build new waves by using some basic
waveforms.
Thus, composite wave form can be the addition
of DC levels of wave, ao
x(t) + ao
y(t) and an
x(t) with
an
y(t) and bn
x(t) with bn
y(t) for two waves x(t) and
y(t)
Basic wave forms are given in Table 15.1 (pp. 765)
Ed. 10 Irwin BECA

20. Frequency Spectrum Construction

21. Thanks
• http://eedmd.weebly.com/ca2/
• MS Teams: EE-201 Circuit Analysis II (Code: kv0slqu)
• http://slideshare.com/jazzofizia/