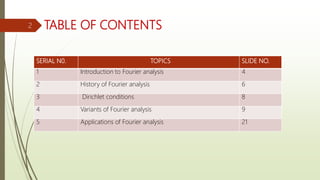
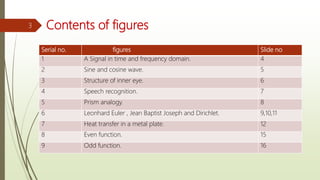
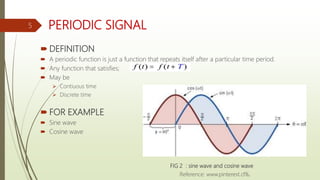
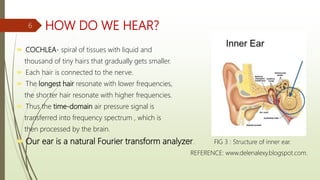
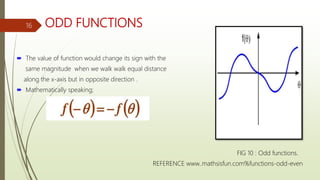
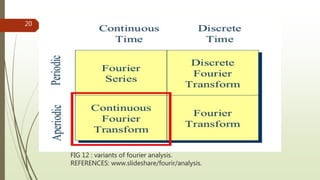
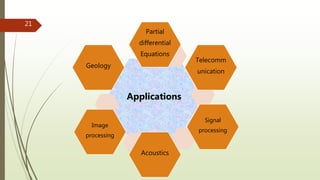
This document provides an overview of Fourier analysis in 3 paragraphs or less: Fourier analysis is a method of representing periodic and aperiodic functions as the sum of trigonometric functions like sines and cosines. It was developed by Joseph Fourier who showed that any signal could be represented as a sum of pure tones. The Fourier transform converts signals between the time and frequency domains, allowing signals to be analyzed by their frequency content. Fourier analysis has applications in fields like signal processing, image processing, acoustics, telecommunications, partial differential equations, geology and more. It provides the foundation for understanding how signals are represented and processed in both continuous and discrete settings.

1. FOURIER ANALYSIS
• PRESENTED TO : DR MUHAMMAD WASEEM MUMTAZ
• PRESENTED BY : AYZA JABEEN
• DEPARTMENT OF CHEMISTRY
• UNIVERSITY OF GUJRAT

2. TABLE OF CONTENTS
SERIAL N0. TOPICS SLIDE NO.
1 Introduction to Fourier analysis 4
2 History of Fourier analysis 6
3 Dirichlet conditions 8
4 Variants of Fourier analysis 9
5 Applications of Fourier analysis 21
2

3. Contents of figures
Serial no. figures Slide no
1 A Signal in time and frequency domain. 4
2 Sine and cosine wave. 5
3 Structure of inner eye. 6
4 Speech recognition. 7
5 Prism analogy. 8
6 Leonhard Euler , Jean Baptist Joseph and Dirichlet. 9,10,11
7 Heat transfer in a metal plate. 12
8 Even function. 15
9 Odd function. 16
3

4. FOURIER ANALYSIS
 Method of defining periodic functions as well as aperiodic functions in terms of
trigonometric sums.
 Method gets its name from Jean Baptist Joseph Fourier.
 He showed that any signal could be made up by adding together a series of pure
tones of (sine wave) of appropriate amplitude and time.
FIG 01: this figure shows the signal in frequency and time domain.
Reference: https;//towardsdatascience-fourier-transformation-com
4

5. PERIODIC SIGNAL
 DEFINITION
 A periodic function is just a function that repeats itself after a particular time period.
 Any function that satisfies;
 May be
 Contiuous time
 Discrete time
 FOR EXAMPLE
 Sine wave
 Cosine wave
FIG 2 : sine wave and cosine wave
Reference: www.pinterest.cl%.
5

6. HOW DO WE HEAR?
 COCHLEA- spiral of tissues with liquid and
thousand of tiny hairs that gradually gets smaller.
 Each hair is connected to the nerve.
 The longest hair resonate with lower frequencies,
the shorter hair resonate with higher frequencies.
 Thus the time-domain air pressure signal is
transferred into frequency spectrum , which is
then processed by the brain.
 Our ear is a natural Fourier transform analyzer. FIG 3 : Structure of inner ear.
REFERENCE: www.delenalexy.blogspot.com.
6

7. TIME DOMAIN
 For example: speech recognition
 Difficult to differentiate between
different sounds in time domain.
FIG 4 : Segment of sound.
Reference: www.researchgate.com
7

8. PRISM ANALOGY
 A prism which splits white light into a spectrum
of colors.
 White light consists of all frequencies mixed
together.
 The prism breaks them apart so we can see
the separate frequencies.
FIG 5 : prism analogy.
REFERENCE: www.slideshare.net.brief-review-of-fourierppt
8

9. HISTORY
 LEONHARD EULAR (1748)
 The configurations of a vibrating string can be
expressed as a linear combination of normal modes
is a string.
 JOSEPH – LOUIS LAGRANGE
 It is impossible to represent signal with corners as
trigonometric sums.
FIG 6 : Leonhard Euler.
REFERENCES: www.Wikipedia.com/history/fourier
9

10. JEAN BAPTIST JOSEPH FOURIER
 French mathematician , Jean Baptist joseph Fourier in 1807
gave the Fourier analysis.
 He worked on propagation and diffusion of heat in
metal bodies.
 He gave the mathematical expressions for heat transfer.
 First announcement was made before French academy of
science.
 Sylvester François Lacroix, Gaspard monger, Pierre Simon
Laplace , joseph louis Lagrange were hired.
 The analytical theory of heat published in Day
 France in 1822.
FIG7 : Jean Baptist Joseph Fourier.
REFERENCES: www.Wikipedia.com.fourier/analysis.
10

11. JOHANN PETER GUSTAY DIRICHLET
 He in 1829 provided precise conditions under which a
periodic signal can be expressed as Fourier series.
 It is famously known as Dirichlet condition.
 F(x) must be periodic, finite and single valued every where.
 It should have finite number of discontinuity to be a periodic
function.
 It should have finite number of maxima and minima.
11

12. FOURIER SERIES
DEFINITION
 It is an expansion of a periodic function in
terms of an infinite sum of sines and cosines.
 Infinite sum of
sine wave + cosine wave = Fourier series
EXPRESSIONS FIG 8 : HEAT TRANSFER IN A METAL
PLATE
 Reference: www.slideshare.net-Ffourier-
series--by- gle.cmd-nazmul-islam&psig md-nazmul-
islam&psigv
12

13. CONTI………
 Fourier series in terms of an even function f(θ) is expressed in terms of cosine
waves.
 Fourier series in terms of an odd function is expressed in terms(θ) of sine waves.
13

14. EULER’S FORMULA
The Fourier series for the function f(x) in the interval a<x <a+2π is given by:
The a0 , an and bn are called the Fourier coefficients.
14

15. EVEN FUNCTIONS
 The value of the function would be the same when
we walk equal distances along the x-axis in in opposite direction.
 Mathematically speaking
F FIG 9 : Even
function.
REFERENCE: www..mathsisfun.com%functions-odd-even
15

16. ODD FUNCTIONS
 The value of function would change its sign with the
same magnitude when we walk walk equal distance
along the x-axis but in opposite direction .
 Mathematically speaking;
FIG 10 : Odd functions.
REFERENCE www..mathsisfun.com%functions-odd-even
16

17. FOURIER TRANSFORM
 The representation of non- periodic functions as linear combination of
sinusoids is famously known as Fourier transform.
 It is used to find frequency contained by given time domain signal.
 Frequency is the no. of occurrences of a repeating event per unit time.
 It converts one function into another without the loss of energy.
 Mathematically: FT
 x(t) x(f)
17

18. DISCRETE FOURIER TRANSFORM
 DFT is used for analyzing discrete-time finite duration signals in the frequency
domain.
 Discrete time data sets are converted into discrete frequency representation.
 Mathematically,
the DFT of discrete time sequence x(n) is denoted by x(k). It is given by,
Here k=0,1,2,……..N-1
Since this summation is taken for ‘N’ points ,it is called ‘N’ point DFT.
18

19. CONTINUOUS FOURIER TRANSFORM
 It turns out a large class of aperiodic signals can also be written as linear
combination of trigonometric sums.
 It deals with continuous time aperiodic signals.
19

20. FIG 12 : variants of fourier analysis.
REFERENCES: www.slideshare/fourir/analysis.
20

21. 21
Applications
Partial
differential
Equations
Telecomm
unication
Signal
processing
Acoustics
Image
processing
Geology

22. References
 https;//whatis.techtarget.com/definition/fourier( visited at 9:13pm , 27/11/2019)
 https;//en.m.Wikipedia.org/wiki/fourier analysis (visited at 10:43am , 27/11/2019)
 https;//www.math.purdue.edu/academic/files (visited at 8:12pm ,28/11/2019)
 https;// www.Britannica.com/science (visited at 9:31pm , 28/11/2019)
 https;//jegilles.sdsu.edu/doc/fouriercours(visited at 9:40 pm , 29/11/2019)
 https;//www.math.bgu.ac.il/leonid/code/schoenstadt fourier pdf(visited at 10: 13pm 30/11/2019)
22