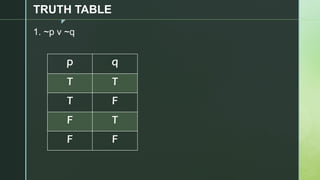
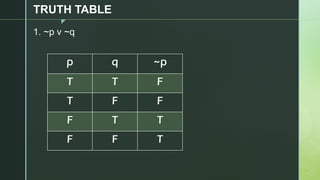
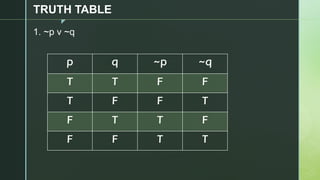
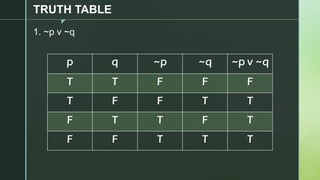
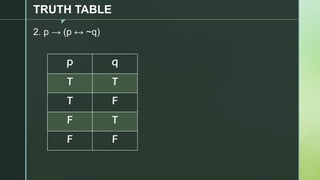
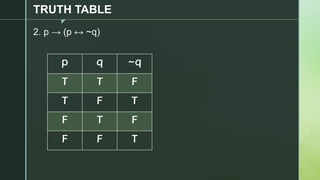
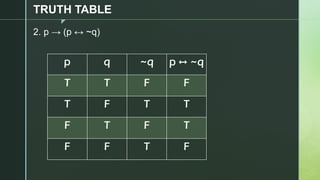
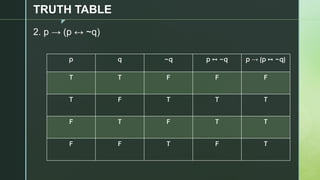
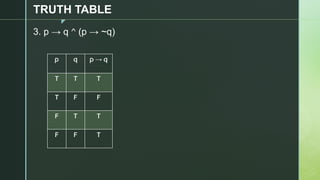
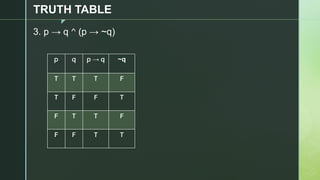
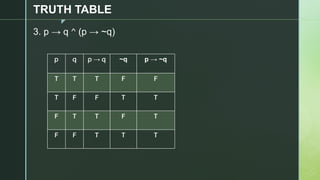
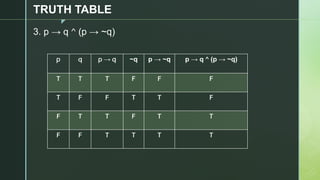
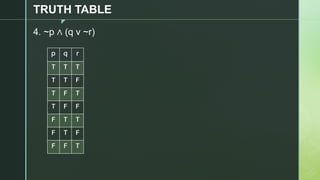
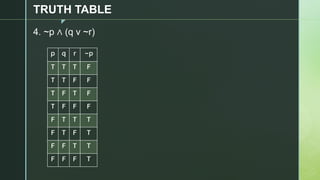
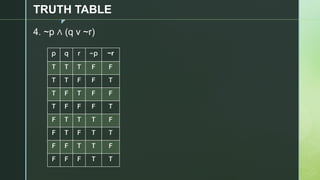
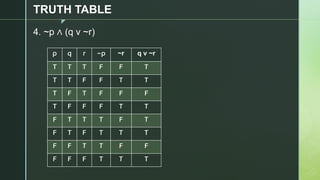
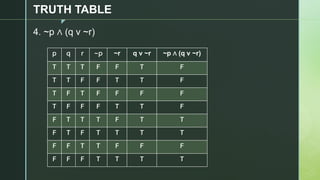
This document discusses truth tables and their use in propositional logic. It provides examples of constructing truth tables for various logical statements involving connectives like conjunction, disjunction, implication, equivalence and negation. The document includes truth tables for the statements ~p v ~q, p → (p ↔ ~q), p → q ^ (p → ~q) and ~p ∧ (q v ~r). It concludes with exercises asking the reader to construct truth tables for additional statements.

1. z
FORMAL LOGIC
Discrete Structures I
FOR-IAN V. SANDOVAL

2. z
Lesson 3
TRUTH TABLES
Source: Google Images

3. z
LESSON OBJECTIVES
❑ Construct truth table for propositional logic

4. z
TRUTH TABLE
1. ~p v ~q
p q
T T
T F
F T
F F

5. z
TRUTH TABLE
1. ~p v ~q
p q ~p
T T F
T F F
F T T
F F T

6. z
TRUTH TABLE
1. ~p v ~q
p q ~p ~q
T T F F
T F F T
F T T F
F F T T

7. z
TRUTH TABLE
1. ~p v ~q
p q ~p ~q ~p v ~q
T T F F F
T F F T T
F T T F T
F F T T T

8. z
TRUTH TABLE
2. p → (p ↔ ~q)
p q
T T
T F
F T
F F

9. z
TRUTH TABLE
2. p → (p ↔ ~q)
p q ~q
T T F
T F T
F T F
F F T

10. z
TRUTH TABLE
2. p → (p ↔ ~q)
p q ~q p ↔ ~q
T T F F
T F T T
F T F T
F F T F

11. z
TRUTH TABLE
2. p → (p ↔ ~q)
p q ~q p ↔ ~q p → (p ↔ ~q)
T T F F F
T F T T T
F T F T T
F F T F T

12. z
TRUTH TABLE
3. p → q ^ (p → ~q)
p q
T T
T F
F T
F F

13. z
TRUTH TABLE
3. p → q ^ (p → ~q)
p q p → q
T T T
T F F
F T T
F F T

14. z
TRUTH TABLE
3. p → q ^ (p → ~q)
p q p → q ~q
T T T F
T F F T
F T T F
F F T T

15. z
TRUTH TABLE
3. p → q ^ (p → ~q)
p q p → q ~q p → ~q
T T T F F
T F F T T
F T T F T
F F T T T

16. z
TRUTH TABLE
3. p → q ^ (p → ~q)
p q p → q ~q p → ~q p → q ^ (p → ~q)
T T T F F F
T F F T T F
F T T F T T
F F T T T T

17. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T

18. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T
T T F

19. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T
T T F
T F T

20. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T
T T F
T F T
T F F

21. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T
T T F
T F T
T F F
F T T

22. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T
T T F
T F T
T F F
F T T
F T F

23. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T

24. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F

25. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r ~p
T T T F
T T F F
T F T F
T F F F
F T T T
F T F T
F F T T
F F F T

26. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r ~p ~r
T T T F F
T T F F T
T F T F F
T F F F T
F T T T F
F T F T T
F F T T F
F F F T T

27. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r ~p ~r q v ~r
T T T F F T
T T F F T T
T F T F F F
T F F F T T
F T T T F T
F T F T T T
F F T T F F
F F F T T T

28. z
TRUTH TABLE
4. ~p ∧ (q v ~r)
p q r ~p ~r q v ~r ~p ∧ (q v ~r)
T T T F F T F
T T F F T T F
T F T F F F F
T F F F T T F
F T T T F T T
F T F T T T T
F F T T F F F
F F F T T T T

29. z
TRUTH TABLES
❑ Enrichment Exercises
Construct the truth table of the following compound
statements.
1. ~p ∧ q
2. (p v q) ∧ ~ (p ∧ q)
3. ~ [(p ∧ q) v ~ (p v q)]
4. (p ↔ ~q) ⊕ (p →q)
5. ~p v (q ∧ ~r)

30. z
• Levin, O. (2019). Discrete Mathematics: An Open Introduction 3rd Edition. Colorado: School of Mathematics Science
University of Colorado.
• Aslam, A. (2016). Proposition in Discrete Mathematics retrieved from https://www.slideshare.net/AdilAslam4/chapter-1-
propositions-in-discrete-mathematics
• Operator Precedence retrieved from http://intrologic.stanford.edu/glossary/operator_precedence.html
REFERENCES