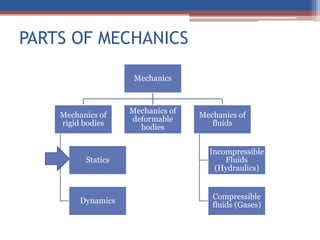
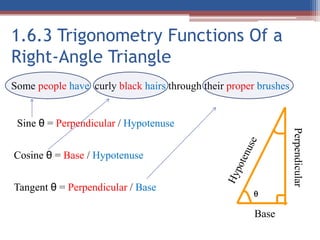
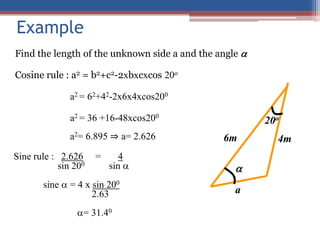
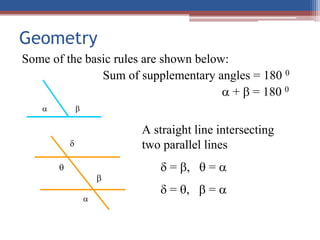
This document provides an introduction to an Engineering Mechanics course. It outlines the course goals, objectives, content, assessment, and textbook. The course aims to introduce concepts of forces, moments, and analytical skills for two and three dimensional systems. Upon completion, students should be able to determine force systems, centroids, and apply equilibrium concepts. The course covers topics like forces, moments, trusses, and beams. Student assessment includes assignments, quizzes, and exams. Rules for the course require high attendance, on-time assignments, and prohibit cell phone use during class.

1. ENGINEERING MECHANICS
COURSE INTRODUCTION

2. Details of Lecturer
• Course Lecturer: Dr. Qazi Samiullah
• Qualification: PhD Structural Engineering
(INSA Lyon, France)
• Room Number: 14, Admin Block
• Email: qazi.samiullah@ciitwah.edu.pk

3. COURSE GOALS
• This course has two specific goals:
• To introduce students to basic concepts of force,
couples and moments in two and three
dimensions.
• To develop analytical skills relevant to the areas
mentioned in above.

4. COURSE OBJECTIVES
Upon successful completion of this course, students
should be able to:
• Determine the resultant of coplanar and space force
systems.
• Determine the centroid and center of mass of plane
areas and volumes.
• Distinguish between concurrent, coplanar and space
force systems.
• Draw free body diagrams.

5. COURSE OBJECTIVES CONTD.
• Analyze the reactions and forces induces in
coplanar and space systems using equilibrium
equations and free body diagrams.
• Determine friction forces and their influence
upon the equilibrium of a system.
• Apply sound analytical techniques and logical
procedures in the solution of engineering
problems.

6. Course Content
• Introduction
• Forces and Moments
• Equilibrium of Rigid bodies
• Geometrical Properties of Plane Areas
• Friction
• Virtual Work (Significance and Applications)
• Analysis of structures (Trusses, Frames and
Machines)
• Forces in Beams

7. Course Textbook
• Text Book
Engineering Mechanics by J.L. Miriam, 5th ed.
• Reference Books
1. Engineering Mechanics – Statics and Dynamics by
R.C. Hibbeler.
2. Engineering Mechanics – Statics and Dynamics by
J.L. Meriam & L.G. Kraige.
3. Vector Mechanics for Engineers – Statics by
Ferdinand P. Beer and E. Russell Johnston Jr.

8. RULES TO BE FOLLOWED
• 80% attendance is must. Otherwise no exam.
• Come in class on time. Otherwise absent.
– 10 minutes relaxation in case of emergency.
• Submit assignments on time.
– Negative 2 (-2) marks/day delay
– After 2 days , it will not be counted.
• Quiz will not be repeated. Absent student will get zero marks.
• Cell phone should be on silent. Preferably switched off.
– Should NOT attend at all.
• Contact me only in office hours.(xx to xx). Alternately email
me. No phone calls.

9. Course Assessment

10. ENGINEERING STATICS
CHAPTER ONE:
INTRODUCTION

11. 1.1 MECHANICS
• It deals with the study and prediction of the state
of rest or motion of particles and bodies under
the action of forces
• Why we study mechanics?
This science form the groundwork for further study
in the design and analysis of structures

12. PARTS OF MECHANICS
Mechanics
Mechanics of
rigid bodies
Statics
Dynamics
Mechanics of
deformable
bodies
Mechanics of
fluids
Incompressible
Fluids
(Hydraulics)
Compressible
fluids (Gases)

13. 1.2 STATICS
• Statics is the study of forces on rigid bodies
which are at rest or moving at a constant
velocity, and the forces are in balance, or in
static equilibrium.
▫ Rigid Body: the relative movement between its
parts are negligible
• Dynamics is the study of forces on bodies with
accelerated motion.

14. 1.3 Fundamental Concepts
Space - associated with the notion of the position of a point P
given in terms of three coordinates measured from a reference
point or origin.
Time - definition of an event requires specification of the time
and position at which it occurred.

15. 1.3 Fundamental Concepts Contd
• Mass - used to characterize and compare bodies,
e.g., response to earth’s gravitational attraction
and resistance to changes in translational
motion.
• Force - represents the action of one body on
another. A force is characterized by its point of
application, magnitude, and direction, i.e., a
force is a vector quantity.

16. 1.3 Fundamental Concepts Contd
Idealizations
• Particles
– Consider mass but neglect size
• Rigid Body
– Neglect material properties

17. 1.4 Fundamental Principles
• Newton’s First Law: If the resultant force on a
particle is zero, the particle will remain at rest or
continue to move in a straight line.
• Newton’s Second Law: A particle will have an
acceleration proportional to a nonzero resultant
applied force.
• Newton’s Third Law: The forces of action and
reaction between two particles have the same
magnitude and line of action with opposite sense.
• Newton’s Law of Gravitation: Two particles are
attracted with equal and opposite forces,
a
m
F



2
2
,
R
GM
g
mg
W
r
Mm
G
F 



18. 1.5 Systems of Units
• Kinetic Units: length, time,
mass, and force.
• Three of the kinetic units are
basic units: length, time, and
mass
• The fourth unit, force is derived
unit, must have a definition
compatible with Newton’s 2nd
Law,
a
m
F



•International System of Units (SI):
The basic units are length, time, and mass
which are arbitrarily defined as the meter
(m), second (s), and kilogram (kg).
•Force is the derived unit,
  







2
s
m
1
kg
1
N
1
ma
F

19. Multiples or submultiples of SI used
Multiples Submultiples
1 kilogram is 1 kg or 103 g 1 millimeter is 1 mm or 10-3 m
1 megagram is 1 Mg or 106 g. 1 micrometer is 1μm or 10-6m
1 gigagram is 1 Gg or 109g 1 nanometer is 1nm or 10-9m

20. 1.6 Mathematics Required
The followings are the mathematics skills that are
important for this module:
• Quadratic equations
• Simultaneous equations
• Trigonometry functions of a right-angle triangle
• Sine and cosine rules

21. 1.6.1 Quadratic equations
• The equation has the standard form as follows
𝑎𝑥2 + 𝑏𝑥 + 𝐶 = 0
• The standard solution to this equation is
𝑥 =
−𝑏± 𝑏2−4𝑎𝑐
2𝑎

22. Example
• Solve for x in the equation 5x2+12x-2=0
▫ Comparing with equation 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
a= 5, b= 12 & c= -2
▫ The standard solution to this equation is
𝑥 =
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
x=+0.156 or – 2.56

23. 1.6.2 Simultaneous Equation
The equation has two unknowns x and y in the form of
ax + by + c = 0
px + qy + r = 0
Example
Find the values of x and y satisfying the given
equations:
4x + 3y + 10 = 0 ….. (1)
20x + 30y + 5 = 0 ….. (2)
There are two methods to solve these equations

24. Method of Substitution
We can start by expressing x in terms of y, or y in terms of x.
Let us choose to express x in terms of y, thus from (1)
𝑥 =
−3𝑦−10
4
…… (3)
Substituting (3) into (2) , yielding
20 × (
−3𝑦−10
4
)+30y +5=0
-15y -50 + 30y + 5 = 0
15y – 45 = 0
y = 3
To find x, substitute the value of y into (3)
𝑥 =
−3×3−10
4
= −4.75

25. Method of Elimination
This method looks for a way to eliminate one of
the unknowns.
This can be done by making the constant factor of
that unknown or variable the same in both
equations by multiplying or dividing one equation
by a selected constant:

26. 4x + 3y + 10 = 0 …… (1)
20x + 30y + 5 = 0 ….. (2)
Divide (2) by 5
4x + 6y + 1 = 0 …. (3)
Subtract (3) by (1)
3y - 9 = 0
y = 3
Substitute the value of y into (1) or (2)
4x + 3(3) + 10 = 0
4x = - 9 - 10
x = - (19/4)= -4.75
Method of Elimination Contd

27. 1.6.3 Trigonometry Functions Of a
Right-Angle Triangle
Some people have curly black hairs through their proper brushes
Sine θ = Perpendicular / Hypotenuse
Base
Perpendicular

Cosine θ = Base / Hypotenuse
Tangent θ = Perpendicular / Base

28. 1.6.4 Sine And Cosine Rules
• For triangles that are not right-angle, the
following two laws are important
Sine Rule a = b = c
sin  sin  sin 
Cosine Rule a2 = b2 + c2 – 2bc cos 
b2 = a2 + c2 – 2ac cos 
c2 = a2 + b2 – 2ab cos 

29. • If the cosine rule is applied to a right-angle
triangle where  = 900
b
c
 
a2 = b2 + c2 – 2bc cos 90 0
Since cos 900 = 0
a2 = b2 + c2 (Pythagoras Theorem)

30. Example
Find the length of the unknown side a and the angle 
Cosine rule : a2 = b2+c2-2xbxcxcos 20o
a2 = 62+42-2x6x4xcos200
a2 = 36 +16-48xcos200
a2= 6.895 ⇒ a= 2.626
Sine rule : 2.626 = 4
sin 200 sin 
sine  = 4 x sin 200
2.63
= 31.40

20o
6m 4m
a

31. Check : 42 = 2.6262 + 62 - 2x2.63x6xcos 
cos  = 2.6262 + 62 – 42
2x2.626x6
cos  = 0.8535
 = 31.4 0

32. Geometry
Some of the basic rules are shown below:
Sum of supplementary angles = 180 0
 +  = 180 0
 




A straight line intersecting
two parallel lines
 = ,  = 
 = ,  = 

33. Similar triangles
AB = BC = AC
AD DE AE
Hence if AB = 6, AD = 3 and BC = 4,
Then, DE
6 = 4
3 DE
DE = (3 x 4)
6
= 2
B
C
D
A
E
triangles ABC and ADE

34. Thank you
Questions ?