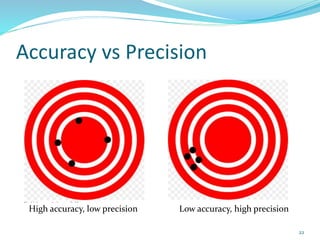
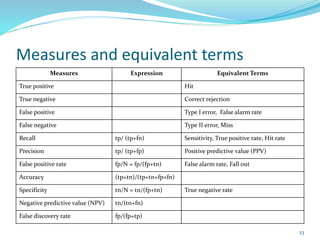
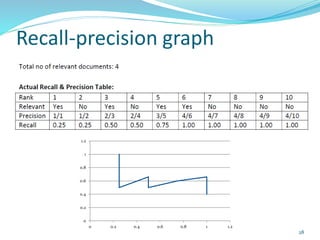
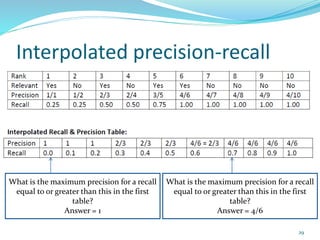
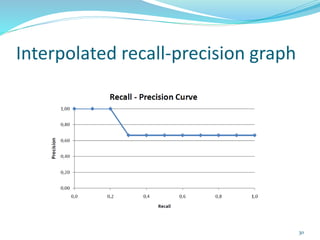
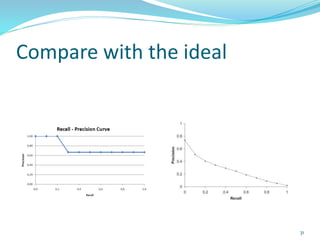
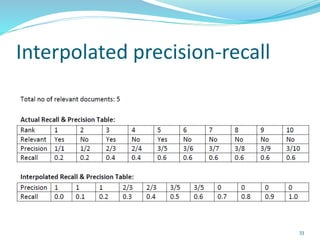
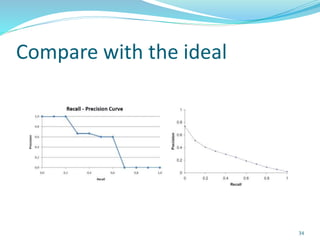
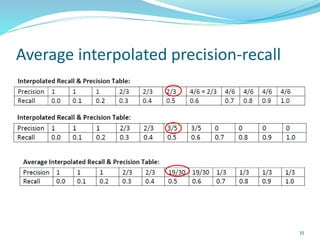
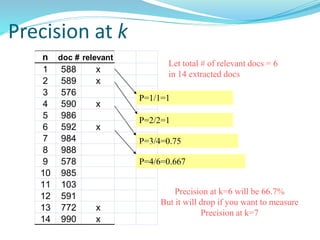
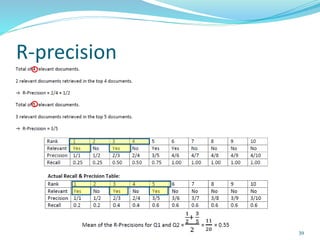
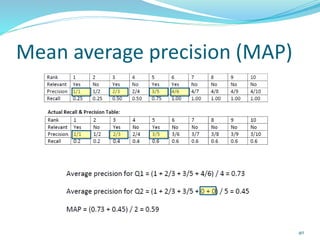
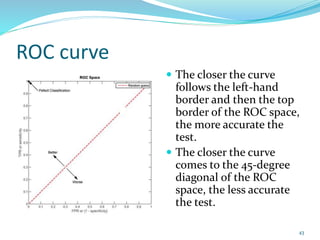
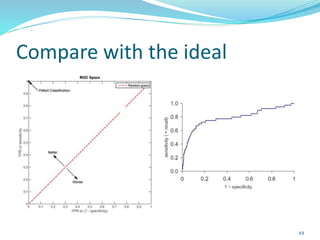
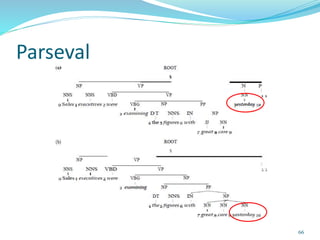
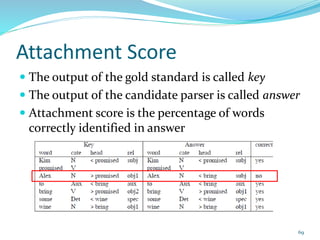
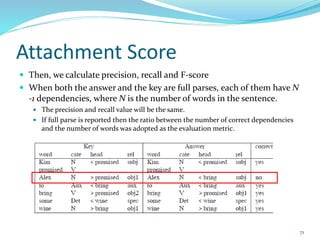
This document discusses various evaluation measures used in information retrieval and natural language processing. It describes precision, recall, and the F1 score as fundamental measures for unranked retrieval sets. It also covers averaged precision and recall, accuracy, novelty and coverage ratios. For ranked retrieval sets, it discusses recall-precision graphs, interpolated recall-precision, precision at k, R-precision, ROC curves, and normalized discounted cumulative gain (NDCG). The document also discusses agreement measures like Kappa statistics and parses evaluation measures like Parseval and attachment scores.

1. Rushdi Shams
Department of Computer Science,
University of Western Ontario, Canada
rshams@csd.uwo.ca

2. Presentation overview
 Measures for unranked retrieval sets
 Precision, recall and f-score
 Average precision and recall
 Accuracy
 Novelty and coverage ratio
 Measures for ranked retrieval sets
 Recall-precision graph
 Interpolated recall-precision graph
 Precision at k
 R-precision
 ROC
 Normalized Discounted Cumulative Graph (NDCG)
 Agreement measures
 Kappa statistics
 Hooper (Jaccard’s co-efficient), Rolling (Dice co-efficient) and Cosine measures
 Parser evaluation measures
 Parseval for syntactic parser evaluation
 Attachment score for dependency parser evaluation
2

4. Precision and Recall
 The two most frequent and basic measures in
information retrieval effectiveness
4

5. Precision and Recall
 The notions are much clearer with a contingency
table-
5

6. Precision and Recall
 Graphically,
6

7. Ways to interpret precision
 A measure of the ability of a system to present only
relevant items
 The fraction of correct instances among all instances
that the algorithm believes to belong to the relevant
set
 It is a measure of exactness or fidelity
 It tells how well a system weeds out what you don't
want
 Says nothing about the number of false negatives
7

8. Ways to interpret recall
 A measure of the ability of a system to present all
relevant items
 The fraction of correct instances among all instances
that actually belong to the relevant set
 It is a measure of completeness
 It tells how well a system performs to get what you
want
 Says nothing about the number of false positives
8

9. Precision or recall?
 Typical web surfers would like every result of the
search engine on the first page to be relevant (high
precision)
 Do they bother if the search engine brings all the
relevant documents (high recall)?
 Individuals searching their hard disks are often
interested in high recall searches
9

10. F-Score
 A single measure that trades off precision versus recall
is the F measure, which is the weighted harmonic
mean of precision and recall
10

11. F-Score
 The default balanced F measure equally weights
precision and recall, which means making
 α = 1/2 or
 β = 1
 The equation of F-Score becomes
11

12. F-Score
 However, using an even weighting is not the only
choice
 Values of β < 1 emphasize precision
 while values of β > 1 emphasize recall.
12

13. F-Score
Say ,
P = 16.20
R = 12.63
If β = 3,
F-Score = 12.91 (closer to recall)
If β = 0.3,
F-Score = 15.82 (closer to precision)
13

14. Why Harmonic Mean?
 Reason 1
 Say a search can return all the documents with a high
recall of 100%
 But when you use it, it gives you 1 document relevant in
10,000 documents (low precision of 0.01%)
 If you take arithmetic mean, you will get the F-score
about 50%.
 If you take harmonic mean, you will get the F-score
0.02%
14

15. Why Harmonic Mean?
 Reason 2
 Harmonic mean
is always less than
or equal to the
arithmetic mean
and the
geometric mean.
 When the values
of two numbers
differ greatly, the
harmonic mean
is closer to their
minimum than
to their
arithmetic mean 15

16. Why Harmonic Mean?
 Reason 3
 Precision and recall are ratios.
 When you use ratios to calculate average, the most
suitable measure is harmonic mean
16

17. Average precision and recall
 Say, on n datasets , you have p1, p2…pn precisions and r1,
r2… rn recalls of your system.
 What is the average precision and recall of your system?
 Macro averaging method:
 computes precision/recall for each test instance first
 then averages these statistics over all instances in the
reference standard
 Micro averaging method:
 The micro-averaging method represents the results where
true positives, false positives and false negatives are added up
across all test instances first
 then these counts are used to compute the statistics
17

18. Average precision and recall
Say, your system has the following performance on two
datasets
tp1 = 10, fp1 = 5, fn1 = 3, p = 66.67, r = 76.92
tp2 = 20, fp2 = 4, fn2 = 5, p = 83.33, r = 80.00
Macro p = (66.67 + 83.33)/2 = 75
Macro r = (76.92+80.00)/2 = 78.46
Micro p = (10+20)/[(10+20)+(5+4)]= 76.92
Micro r = (10+20)/[(10+20)+(3+5)] = 78.94
18

19. Average precision and recall
 The micro-averaging method favors large
categories with many instances
 The macro-averaging method shows how the
classifier performs across all categories
19

20. Accuracy
 An obvious alternative that may occur to the reader is
to judge an information retrieval system by its
accuracy
 It is the fraction of its classifications that are correct.
20

21. Accuracy
 There is a good reason why accuracy is not an appropriate
measure for information retrieval problems.
 In almost all circumstances, the data is extremely skewed:
normally over 99.9% of the documents are in the
nonrelevant category.
 A system tuned to maximize accuracy can appear to
perform well by simply deeming all documents
nonrelevant to all queries.
 Even if the system is quite good, trying to label some
documents as relevant will almost always lead to a high rate
of false positives.
21

22. Accuracy vs Precision
High accuracy, low precision Low accuracy, high precision
22

23. Measures and equivalent terms
Measures Expression Equivalent Terms
True positive Hit
True negative Correct rejection
False positive Type I error, False alarm rate
False negative Type II error, Miss
Recall tp/ (tp+fn) Sensitivity, True positive rate, Hit rate
Precision tp/ (tp+fp) Positive predictive value (PPV)
False positive rate fp/N = fp/(fp+tn) False alarm rate, Fall out
Accuracy (tp+tn)/(tp+tn+fp+fn)
Specificity tn/N = tn/(fp+tn) True negative rate
Negative predictive value (NPV) tn/(tn+fn)
False discovery rate fp/(fp+tp)
23

24. Some other measures
 Novelty ratio
 The proportion of items retrieved and judged relevant
by the user and of which they were previously unaware.
 Ability to find new information on a topic.
 Coverage ratio
 The proportion of relevant items retrieved out of the
total relevant documents known to a user prior to the
search.
24

26. Introduction
 Precision, recall, and the F measure are set-based
measures.
 They are computed using unordered sets of
documents.
 We need to extend these measures if we are to evaluate
the ranked retrieval results
 standard with search engines.
26

28. Recall-precision graph
28
0
0.2
0.4
0.6
0.8
1
1.2
0 0.2 0.4 0.6 0.8 1 1.2

29. Interpolated precision-recall
29
What is the maximum precision for a recall
equal to or greater than this in the first
table?
Answer = 1
What is the maximum precision for a recall
equal to or greater than this in the first
table?
Answer = 4/6

30. Interpolated recall-precision graph
30

31. Compare with the ideal
31

33. Interpolated precision-recall
33

34. Compare with the ideal
34

35. Average interpolated precision-recall
35

36. Compare with the ideal
36

37. Precision at k
 This leads to measuring precision at fixed level lower
than the retrieved results
 Such as ten (precision at 10) or thirty documents
(precision at 30)
 Useful when you don’t know the number of relevant
documents
 Least stable of the commonly used measures
 Does not average well
37

38. P=3/4=0.75
Precision at k
n doc # relevant
1 588 x
2 589 x
3 576
4 590 x
5 986
6 592 x
7 984
8 988
9 578
10 985
11 103
12 591
13 772 x
14 990 x
Let total # of relevant docs = 6
in 14 extracted docs
P=1/1=1
P=2/2=1
P=4/6=0.667
Precision at k=6 will be 66.7%
But it will drop if you want to measure
Precision at k=7

39. R-precision
39

40. Mean average precision (MAP)
40

41. ROC curve
 Stands for Receiver Operating Characteristics
 Plots true positive rate/ sensitivity/ recall against false
positive rate or (1-specificity)
41

42. ROC curve
 Specificity
 A sniffer dog looking for drugs would have a low specificity if it is
often led astray by things that aren't drugs - cosmetics or food, for
example.
 Specificity can be considered as the percentage of times a test will
correctly identify a negative result.
 Also called true negative rate
 False positive rate
 1 – specificity
 1 – (tn/(fp + tn)) = fp/(fp + tn)
42

43. ROC curve
 The closer the curve
follows the left-hand
border and then the top
border of the ROC space,
the more accurate the
test.
 The closer the curve
comes to the 45-degree
diagonal of the ROC
space, the less accurate
the test.
43

44. Compare with the ideal
44

45. Area under the ROC curve
 There are many tools that can give you the area under
the curve (AUC) of ROC
 If you don’t understand the ability of your system from
ROC curve alone, you can use the AUC instead
 .90-1 = excellent
 .80-.90 = good
 .70-.80 = fair
 .60-.70 = poor
 .50-.60 = fail
45

46. Cumulative gain
 Say you have extracted 6 documents
 The relevance of each document is to be judged on a
scale of 0-3 with 0 meaning irrelevant, 3 meaning
completely relevant, and 1 and 2 meaning "somewhere
in between".
 The order of your extraction be
 D1,D2,D3,D4,D5,D6
 Your score on them be
 3,2,3,0,1,2
 The Cumulative Gain of this search result listing is:
46

47. Discounted Cumulative Gain (DCG)
 So the DCG6 of this ranking is:
47

48. Normalized DCG (NDCG)
 The performance of this query to another is
incomparable
 since the other query may have more results, resulting in
a larger overall DCG which may not necessarily be
better.
 In order to compare, the DCG values must be
normalized.
48

49. NDCG
 To normalize DCG values, an ideal ordering for the
given query is needed.
 One ideal ordering can be the documents in ascending
order of their relevance scores
 3,3,2,2,1,0
 The DCG of this ideal ordering, or IDCG, is then
 IDCG6 = 8.693
 The nDCG for this query is given as:
49

50. 50

51. Kappa measure
 Suppose that you were analyzing data related to people
applying for a grant.
 Each grant proposal was read by two people and each
reader either said "Yes" or "No" to the proposal
 Suppose the data were as follows, where rows are
reader A and columns are reader B
51

52. Kappa measure
 Note that there were 20 proposals that were granted by
both reader A and reader B, and
 15 proposals that were rejected by both readers.
 Thus, the observed percentage agreement is
Pr(a)=(20+15)/50 = 0.70.
52

53. Kappa measure
 To calculate Pr(e) (the probability of random agreement)
we note that
 Reader A said "Yes" to 25 applicants and "No" to 25 applicants.
Thus reader A said "Yes" 50% of the time.
 Reader B said "Yes" to 30 applicants and "No" to 20 applicants.
Thus reader B said "Yes" 60% of the time.
53

54. Kappa measure
 Therefore the probability that both of them would say "Yes"
randomly is 0.50*0.60=0.30 and
 The probability that both of them would say "No" is
0.50*0.40=0.20.
 Thus the overall probability of random agreement is
 Pr("e") = 0.3+0.2 = 0.5.
54

55. Kappa measure
55

56. Inconsistencies with Kappa measure
 In the following two cases there is equal agreement
between A and B (60 out of 100 in both cases) so we
would expect the relative values of Cohen's Kappa to
reflect this.
56

57. Interpretation of Kappa measures
 Kappa is always less than or equal to 1.
 A value of 1 implies perfect agreement and values less than 1
imply less than perfect agreement.
 In rare situations, Kappa can be negative.
 This is a sign that the two observers agreed less than would be
expected just by chance.
 Possible interpretations of Kappa (Altman DG. Practical Statistics for
Medical Research. (1991) London England: Chapman and Hall).
 Poor agreement = Less than 0.20
 Fair agreement = 0.20 to 0.40
 Moderate agreement = 0.40 to 0.60
 Good agreement = 0.60 to 0.80
 Very good agreement = 0.80 to 1.00
57

58. Other agreement measures
 A (or M) and B (or N) are the two sets of extracted terms
 C is the no. of terms common between two sets

60. Common parse tree evaluation measures
 Tree accuracy or Exact match
 1 point if the parse tree is completely right (against the
gold standard), 0 otherwise
 Strictest criterion
 For many potential task, partly right parses are not
much use
 things will not work very well in a database query system if one
gets the scope of operators wrong, and it does not help much that
the system got part of the parse tree right.
60

61. Parseval
 These measures evaluate the component pieces of a
parse
61

62. Parseval
62

63. Parseval
63

64. Parseval
 Charniak shows that according to these measures, one
can do surprisingly well on parsing the Penn by
inducing a vanilla PCFG which ignores all lexical
content
 Success on crossing brackets is helped by the fact that
Penn trees are quite flat.
 To the extent that sentences have very few brackets in
them, the number of crossing brackets is likely to be
small.
64

65. Parseval
 If there is a constituent that attaches very high (in a
complex right-branching sentence), but the parser by
mistake attaches it very low, then every node in the
right-branching complex will be wrong, seriously
damaging both precision and recall, whereas arguably
only a single mistake was made by the parser.
65

66. Parseval
66

68. Types of evaluation
 Exact match
 This is the percentage of completely correctly parsed
sentences.
 The same measure is also used for the evaluation of
constituent parsers.
 Attachment score
 This is the percentage of words that have the correct
head.
68

69. Attachment Score
 The output of the gold standard is called key
 The output of the candidate parser is called answer
 Attachment score is the percentage of words
correctly identified in answer
69

70. Attachment Score
 True Positives: Present in both output
 False Positives: Present in answer but absent in key
 False Negatives: Present in key but absent in answer
Gold Standard (key)Output Candidate (answer) output
70

71. Attachment Score
 Then, we calculate precision, recall and F-score
 When both the answer and the key are full parses, each of them have N
-1 dependencies, where N is the number of words in the sentence.
 The precision and recall value will be the same.
 If full parse is reported then the ratio between the number of correct dependencies
and the number of words was adopted as the evaluation metric.
71

72. Types of attachment score
 Strict evaluation
 Dependency, head and dependent- all must match
 Useful when both of the parsers use same set of
dependency relations
 Relaxed evaluation
 Head and dependent must match but match with
dependency is optional
 Some evaluations report the match of the head in a
dependency
 Useful when the parsers use different set of dependency
relations
72

73. References
 Enormous resources have been collected from Mr.
Google, son of Mrs. Web
 Manning et al. Introduction to Information Retrieval.
Cambridge University Press. 2008
 Manning and Schutze. Foundations of Statistical NLP.
The MIT Press. 1999
73