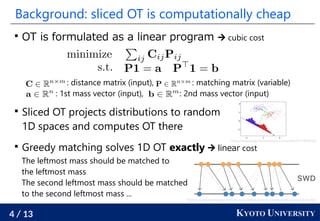
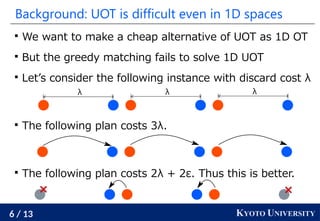
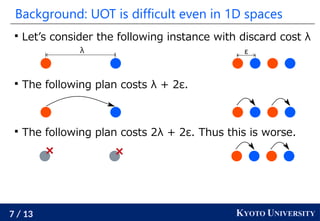
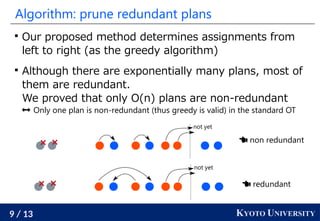
This document presents research by Ryoma Sato of Kyoto University on fast unbalanced optimal transport (UOT) algorithms that efficiently handle the transport of distribution masses while being robust to outliers. It discusses the challenges of UOT in one-dimensional spaces and introduces a new algorithm that reduces the computational complexity to O(n log² n), which is significantly faster than traditional methods. The proposed method extends to tree spaces and demonstrates empirical effectiveness, computing UOT with one million masses in under one second.

1. 1 KYOTO UNIVERSITY
KYOTO UNIVERSITY
Fast Unbalanced Optimal Transport on a Tree
Ryoma Sato
Kyoto University / RIKEN AIP

2. 2 / 13 KYOTO UNIVERSITY
Self Introduction

I am a second year master's student at
Kyoto University

I’m interested in algorithmic aspects of machine
learning and data mining for structured data, including
Graph neural networks:

Ryoma Sato, Makoto Yamada, Hisashi Kashima. Approximation Ratios of
Graph Neural Networks for Combinatorial Problems. NeurIPS 2019.

Ryoma Sato, Makoto Yamada, Hisashi Kashima. Random Features
Strengthen Graph Neural Networks. SDM 2021
Optimal transport:

Ryoma Sato, Makoto Yamada, Hisashi Kashima. Fast Unbalanced Optimal
Transport on a Tree. NeurIPS 2020.
 Today’s topic

3. 3 / 13 KYOTO UNIVERSITY
Background: optimal transport is useful

The optimal transport (OT) distance measures
the discrepancy of two distributions.
We consider discrete distributions in this presentation.

The OT distance is the minimum cumulative
distance that all masses need to travel from
one distribution to another distribution

In generative modeling, a mass is a sample.
discrepancy of model  sample distribution

In text classification, a mass is a word.
 OT does not require the same support  KL divergence
 OT exploits the underground geometry
From Word Embeddings To
Document Distances, ICML 2015

4. 4 / 13 KYOTO UNIVERSITY
Background: sliced OT is computationally cheap

OT is formulated as a linear program  cubic cost

Sliced OT projects distributions to random
1D spaces and computes OT there

Greedy matching solves 1D OT exactly  linear cost
: distance matrix (input), : matching matrix (variable)
: 1st mass vector (input), : 2nd mass vector (input)
The leftmost mass should be matched to
the leftmost mass
The second leftmost mass should be matched
to the second leftmost mass ...
https://www.programmersought.com/article/67174999352/
https://analyticsindiamag.com/how-to-establish-domain-transferability-in-neural-models/

5. 5 / 13 KYOTO UNIVERSITY
Background: unbalanced OT is robust

OT is sensitive to outliers because transporting outliers
becomes the dominating term

Unbalanced OT (UOT) allows to discard and create
masses by paying some penalties
 We can discard outliers  robust to outliers

UOT is also formulated by a linear program
 cubic cost

6. 6 / 13 KYOTO UNIVERSITY
Background: UOT is difficult even in 1D spaces

We want to make a cheap alternative of UOT as 1D OT

But the greedy matching fails to solve 1D UOT

Let’s consider the following instance with discard cost λ

The following plan costs 3λ.

The following plan costs 2λ + 2ε. Thus this is better.
λ λ λ

7. 7 / 13 KYOTO UNIVERSITY
Background: UOT is difficult even in 1D spaces

Let’s consider the following instance with discard cost λ

The following plan costs λ + 2ε.

The following plan costs 2λ + 2ε. Thus this is worse.
λ ε

8. 8 / 13 KYOTO UNIVERSITY
Background: UOT is difficult even in 1D spaces

Although these two instances share the leftmost part,
the leftmost mass in the first instance should be
discarded while that in the second instance should not

The optimal UOT plan cannot be determined locally
 The optimal OT plan is determined locally

Thus the greedy algorithm fails to solve 1D UOT

We proposed how to solve 1D UOT efficiently
λ λ λ
λ ε

9. 9 / 13 KYOTO UNIVERSITY
Algorithm: prune redundant plans

Our proposed method determines assignments from
left to right (as the greedy algorithm)

Although there are exponentially many plans, most of
them are redundant.
We proved that only O(n) plans are non-redundant
 Only one plan is non-redundant (thus greedy is valid) in the standard OT
not yet
not yet
 non redundant
 redundant

10. 10 / 13 KYOTO UNIVERSITY
Algorithm: we solve 1D UOT in O(n log2
n) time

A naive algorithm requires cubic time even with this
(non redundant plan) observation

More algorithmic techniques are required for further
speedup (skipped in this presentation)

Dynamic programming

Fast convex min-sum convolution

Efficient data structure (BBST)

Weighted union heuristics

Finally, we derived a quasi-linear time algorithm
which runs in O(n log2
n) time in the worst case

11. 11 / 13 KYOTO UNIVERSITY
Algorithm: tree UOT generalizes 1D UOT

Our method can be extended to tree spaces
A 1D space (path) is a special case of tree spaces

In text classification, the word
space can be represented by a
word tree. Each mass (word)
travels on the word tree to a
nearby (semantically similar) word.

We can “tree-slice” high dimensional
spaces instead of 1D-slicing,
which captures richer structures
http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/117-hcpc-hierarchical-clustering-on-principal-components-essentials/
a → b

12. 12 / 13 KYOTO UNIVERSITY
Experiments: our algorithm is empirically fast

We confirmed that our algorithm could compute tree
UOT with one million masses within one second

We also confirmed that tree-slicing high dimensional
spaces could approximate the original UOT problem

13. 13 / 13 KYOTO UNIVERSITY
Conclusion: fast computation of tree UOT

Sliced OT is a fast alternative of OT

UOT is a robust variant of OT

1D UOT is more difficult than 1D OT

We proposed an efficient algorithm for 1D UOT for the
first time

Our method can be extended to tree spaces

Our method is empirically fast (1M masses in 1 sec)