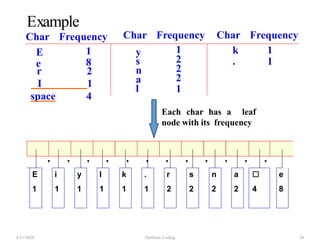
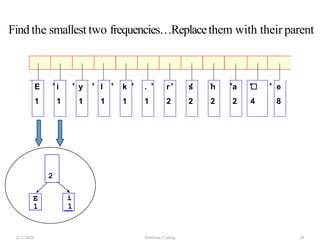
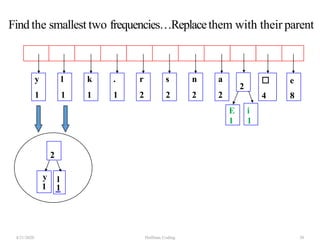
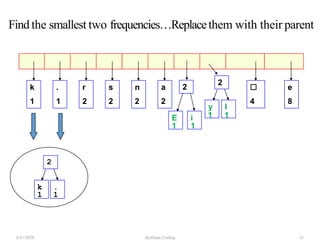
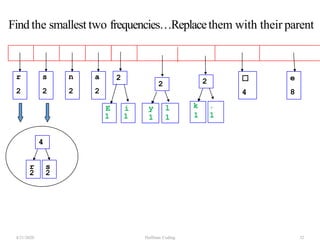
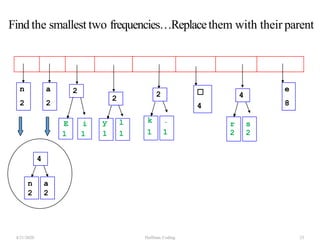
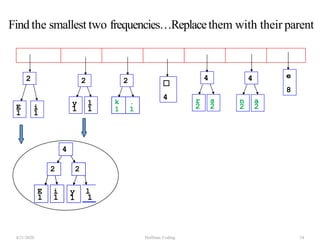
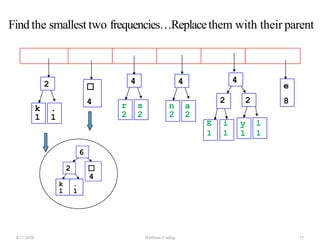
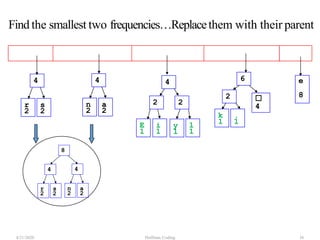
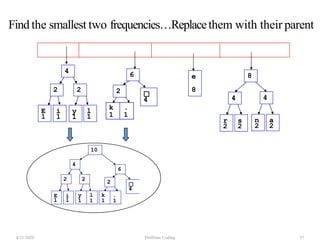
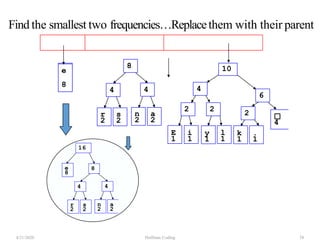
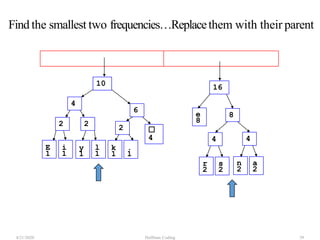
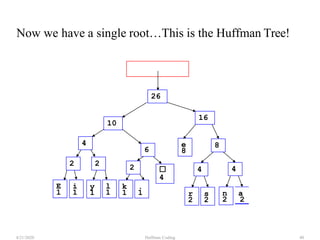
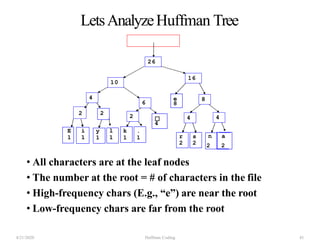
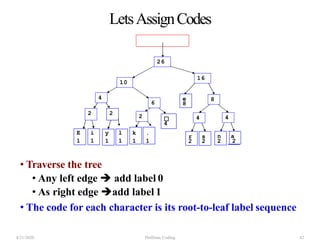
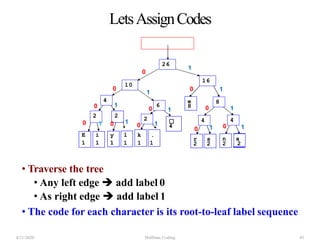
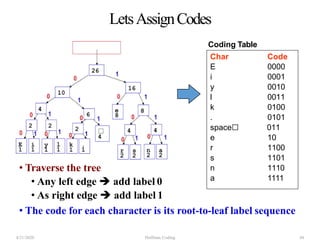
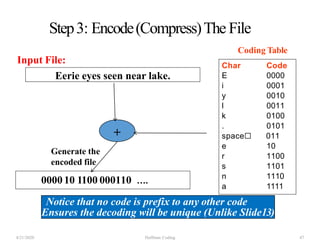
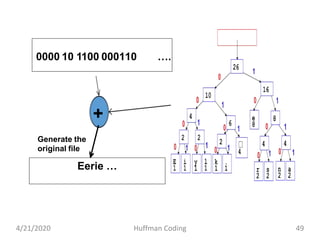
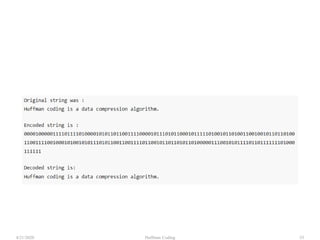
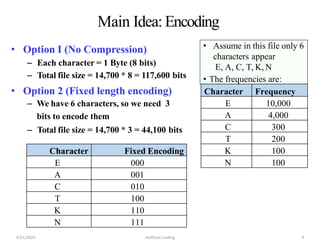
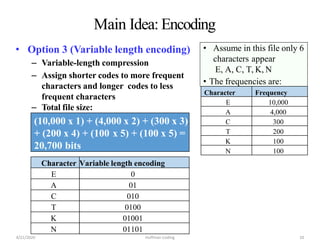
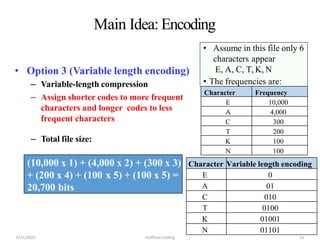
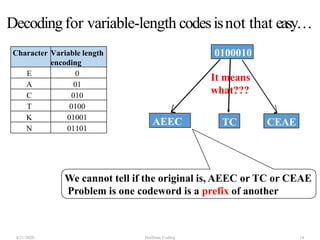
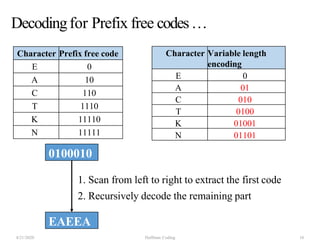
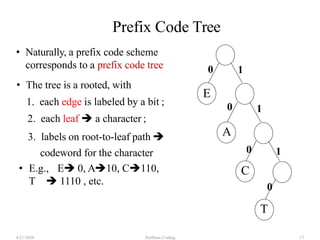
The document discusses Huffman coding, which is a lossless data compression algorithm that uses variable-length codes to encode characters based on their frequency of occurrence. It involves building a Huffman tree by iteratively combining the two lowest frequency nodes and assigning codes to characters based on their paths in the tree. The algorithm is described in 4 steps - getting character frequencies, building the Huffman tree and assigning codes, encoding the data, and decoding the compressed data. Examples are provided to illustrate how the Huffman tree is constructed bottom-up and codes are assigned.

1. Huffman Coding
4/21/2020 Huffman Coding 1

2. Contents:
• Data Compression
• Fixed length encoding
• Variable length encoding
• Prefix Code
• Representing Prefix Codes Using Binary Tree
• Decoding A Prefix Code
• Optimality
• Huffman Coding
• Cost Of Huffman Tree
• Huffman Algorithm and Implementation
4/21/2020 Huffman Coding 2

3. DataCompression
• Use less bits
• Reduce original file size.
• Space-Time complexity trade-off.
• useful - reduce resources usage, suchasdata storage spaceor
transmission capacity.
Compressiontypes:
1.Losslesscompression
2.Lossycompression
4/21/2020 Huffman Coding 3
Using the tools, such as zip, 7zip

4. 4
Bits...Bytes...etc...
Poll Question#1 : How many bits are required to represent 26
characters/ symbols?
A. 26 bits
B. 32 bits
C. 5 bits
D. 8 bits
2 = 26?
2 = 32
5
5 bits are required to represent
26 characters
4/21/2020 Huffman Coding

5. 32-26= 6 characters representation are unused.
e.g. 0= 00000 represents character A
1= 00001 represents character B
...
25= 011001 represents character Z
26= 011010 is unused.
27= 011011 is unused.
28= 011100 is unused.
29 unused.
30 unused.
31 unused.
can be used in future…
4/21/2020 Huffman Coding 5
Bits...Bytes...etc...

6. Huffman Coding4/21/2020 6
2 symbols
1
5 bits are required to represent 26 symbols
2
a
1b =
= 0
c = 0
0
0
1
1 1d =
2 =
2 4 symbols=
2 8 symbols=
3
2 16 symbols=
4
2 32 symbols=
5
Bits...Bytes...etc...

7. Huffman Coding4/21/2020 7
• In ASCII, each English character is represented in the
number of bits (8 bits)
• If a text contains n characters, it takes 8n bits in total to
store the text in ASCII
• E.g. A =
ABC = 8*3= 24 bits
Text file with 14,700 characters will require,
14,700 * 8 = 117,600 bits
Bits...Bytes...etc...
65 = 01000001= 8*1 = 8 bits

8. Main Idea: Encoding
• Assume in this file
only 6 characters
appear
E, A, C, T, K, N
• The frequencies are:
Character Frequency
E 10,000
A 4,000
C 300
T 200
K 100
N 100
Original file
4/21/2020 Huffman Coding 8

9. Main Idea: Encoding
• Assume in this file only 6
characters appear
E, A, C, T, K, N
• The frequencies are:
Character Frequency
E 10,000
A 4,000
C 300
T 200
K 100
N 100
• Option I (No Compression)
– Each character = 1 Byte (8 bits)
– Total file size = 14,700 * 8 = 117,600 bits
• Option 2 (Fixed length encoding)
– We have 6 characters, so we need 3
bits to encode them
– Total file size = 14,700 * 3 = 44,100 bits
Character Fixed Encoding
E 000
A 001
C 010
T 100
K 110
N 111
4/21/2020 Huffman Coding 9

10. Main Idea: Encoding
• Assume in this file only 6
characters appear
E, A, C, T, K, N
• The frequencies are:
Character Frequency
E 10,000
A 4,000
C 300
T 200
K 100
N 100
Character Variable length encoding
E 0
A 01
C 010
T 0100
K 01001
N 01101
• Option 3 (Variable length encoding)
– Variable-length compression
– Assign shorter codes to more frequent
characters and longer codes to less
frequent characters
– Total file size:
(10,000 x 1) + (4,000 x 2) + (300 x 3)
+ (200 x 4) + (100 x 5) + (100 x 5) =
20,700 bits
4/21/2020 Huffman Coding 10

11. 11
Poll Question#2 : The binary code length does not depend on the
frequency of occurrence of characters.
A. True
B. False
4/21/2020 Huffman Coding

12. Main Idea: Encoding
• Assume in this file only 6
characters appear
E, A, C, T, K, N
• The frequencies are:
Character Frequency
E 10,000
A 4,000
C 300
T 200
K 100
N 100
Character Variable length encoding
E 0
A 01
C 010
T 0100
K 01001
N 01101
• Option 3 (Variable length encoding)
– Variable-length compression
– Total file size:
(10,000 x 1) + (4,000 x 2) + (300 x 3)
+ (200 x 4) + (100 x 5) + (100 x 5) =
20,700 bits
4/21/2020 Huffman Coding 12
– Assign shorter codes to more frequent
characters and longer codes to less
frequent characters

13. Decodingfor fixed-length codesismuch easier
Character Fixed
length
encoding
E 000
A 001
C 010
T 100
K 110
N 111
010001100110111000
010 001 100 110 111 000
Divide into 3’s
C A T K N E
Decode
4/21/2020 Huffman Coding 13

14. Decodingfor variable-length codesisnot that easy…
0100010
It means
what???
AEEC TC CEAE
We cannot tell if the original is, AEEC or TC or CEAE
4/21/2020 Huffman Coding 14
Character Variable length
encoding
E 0
A 01
C 010
T 0100
K 01001
N 01101
Problem is one codeword is a prefix of another

15. Huffman Coding4/21/2020 15
• Toavoid the problem, we generally want that each codeword is
NOT a prefix of another
• Such an encoding scheme is called a prefix code, or prefix-free
code
• For a text encoded by a prefix code, we can easily decode it in the
following way :
10100001000101000101000…
1 2
1 Scan from left to right to extract the first code
2 Recursively decode the remaining part

16. Decodingfor Prefix free codes…
0100010
EAEEA
4/21/2020 Huffman Coding 16
Character Prefix free code
E 0
A 10
C 110
T 1110
K 11110
N 11111
Character Variable length
encoding
E 0
A 01
C 010
T 0100
K 01001
N 01101
1. Scan from left to right to extract the first code
2. Recursively decode the remaining part

17. Huffman Coding4/21/2020 17
Prefix Code Tree
• Naturally, a prefix code scheme
corresponds to a prefix code tree
E
0 1
0 1
A
C
0 1
T
0
• The tree is a rooted, with
1. each edge is labeled by a bit ;
2. each leaf  a character ;
3. labels on root-to-leaf path 
codeword for the character
• E.g., E 0, A10, C110,
T  1110 , etc.

18. 18
Poll Question#3 : From the following given tree, what is the code
word for the character ‘a’?
A. 010
B. 100
C. 101
D. 011
4/21/2020 Huffman Coding
0
1
1

19. 19
Poll Question#4 : From the following given tree, what is the
computed codeword for ‘c’?
A. 010
B. 100
C. 110
D. 011
4/21/2020 Huffman Coding
0
1
1

20. Main Idea: Encoding
• Assume in this file only 6
characters appear
E, A, C, T, K, N
• The frequencies are:
Character Frequency
E 10,000
A 4,000
C 300
T 200
K 100
N 100Original file
4/21/2020 Huffman Coding 20
….Construct Optimal Prefix Code Tree

21. • Proposed by Dr. David A. Huffman in 1952
“A Method for the Construction of Minimum Redundancy Codes”
• Applicable to many forms of data transmission
Our example: text files
• Build the optimal prefix code tree, bottom-up in a greedy fashion
Huffman Coding
4/21/2020 Huffman Coding 21

22. • A technique to compress data effectively
• Usually between 20%-90% compression
• Lossless compression
• No information is lost
• When decompress, you get the original file
4/21/2020 Huffman Coding 22
Compressed file
Huffman coding
Original file
Huffman Coding

23. Huffman Coding:Applications
• Saving space
• Store compressed files instead of original files
• Transmitting files or data
• Send compressed data to save transmission time and power
• Encryption and decryption
• Cannot read the compressed file without knowing the “key”
Compressed file
Huffman coding
4/21/2020 Huffman Coding 23
Original file

24. HuffmanCoding
•A variable-length coding for characters
• More frequent characters shorter codes
• Less frequent characters longer codes
•It is not like ASCII coding where all characters
have the same coding length (8 bits)
•Two main questions
1. How to assign codes (Encoding process)?
2. How to decode (from the compressed file, generate
the original file)
(Decoding process)?
4/21/2020 Huffman Coding 24

25. Huffman Algorithm
• Step 1: Get Frequencies
• Scan the file to be compressed and count the occurrence of
each character
• Sort the characters based on their frequency
• Step 2: Build Tree & Assign Codes
• Build a Huffman-code tree (binary tree)
• Traverse the tree to assign codes
• Step 3: Encode (Compress)
• Scan the file again and replace each character by its code
• Step 4: Decode (Decompress)
• Huffman tree is the key to decompress the file
4/21/2020 Huffman Coding 25

26. Step1: GetFrequencies
Eerie eyes seen near lake.
Char Frequency
E
e
1
8
k
.
1
1
r 2
I 1
y
s
n
a
l
1
2
2
2
1
Input File:
4/21/2020 Huffman Coding 26
Char Frequency Char Frequency
space 4

27. Step2: Build Huffman Tree& AssignCodes
• It is a binary tree in which each character is a leaf node
• Initially each node is a separate root
• At each step
• Select two roots with smallest frequency and connect
them to a new parent (Break ties arbitrary) [The greedy
choice]
• The parent will get the sum of frequencies of the two
child nodes
• Repeat until you have one root
4/21/2020 Huffman Coding 27

28. Example
E
1
i
1
y
1
l
1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
Each char has a leaf
node with its frequency
4/21/2020 Huffman Coding 28
Char Frequency
E
e
1
8
k
.
1
1
r 2
I 1
y
s
n
a
l
1
2
2
2
1
Char Frequency Char Frequency
space 4

29. Find the smallest two frequencies…Replacethem with their parent
E
1
i
1
y
1
l
1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
E
1
i
1
2
4/21/2020 Huffman Coding 29

30. E i
1 1
y
1
l
1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
2
y
1
l
1
2
4/21/2020 Huffman Coding 30
Find the smallest two frequencies…Replacethem with their parent

31. E i
1 1
k
1
.
1
r
2
s
2
n
2
a
2
☐
4
e
8
2
y l
1 1
2
k .
1 1
2
4/21/2020 Huffman Coding 31
Find the smallest two frequencies…Replacethem with their parent

32. E i
1 1
r
2
s
2
n
2
a
2
☐
4
e
8
2
y l
1 1
2
k .
1 1
2
r s
2 2
4
4/21/2020 Huffman Coding 32
Find the smallest two frequencies…Replacethem with their parent

33. E i
1 1
n
2
a
2
☐
4
e
8
2
y l
1 1
2
k .
1 1
2
r s
2 2
4
n a
2 2
4
4/21/2020 Huffman Coding 33
Find the smallest two frequencies…Replacethem with their parent

34. E i
1 1
☐
4
e
8
2
y l
1 1
2
k .
1 1
2
r s
2 2
4
n a
2 2
4
E i
2
y l
1 1 1 1
2
4
4/21/2020 Huffman Coding 34
Find the smallest two frequencies…Replacethem with their parent

35. ☐
4
e
82
E i y l
1 1 1 1
2
k .
1 1
2
r s
2 2
4
n a
2 2
4 4
☐
4
k .
1 1
2
6
4/21/2020 Huffman Coding 35
Find the smallest two frequencies…Replacethem with their parent

36. E i
1 1
☐
4
e
8
2
y
1
l
1
2
k .
1 1
2
r s
2 2
4
n a
2 2
4 4 6
r
4
s n a
2 2 2 2
4
8
4/21/2020 Huffman Coding 36
Find the smallest two frequencies…Replacethem with their parent

37. E i
☐
4
e
82
y l
1 1 1 1
2
k .
1 1
2
r s
2 2
4
n a
2 2
4
4
6 8
E i
1 1
☐
4
2 2
y l k .
1 1 1 1
2
4
6
10
4/21/2020 Huffman Coding 37
Find the smallest two frequencies…Replacethem with their parent

38. ☐
4
e
8
2 2
E i y l k .
1 1 1 1 1 1
2r s
2 2
4
n a
2 2
4 4
6
8 10
e
8
r s
4
n a
2 2 2 2
4
8
16
4/21/2020 Huffman Coding 38
Find the smallest two frequencies…Replacethem with their parent

39. ☐
4
e
82 2
E i y l k .
1 1 1 1 1 1
2
r s
4
n a
2 2 2 2
4
4
6
8
10 16
4/21/2020 Huffman Coding 39
Find the smallest two frequencies…Replacethem with their parent

40. ☐
4
e
8
2 2
E i y l k .
1 1 1 1 1 1
2
2 2
4
r s n a
2 2
4
4
6
8
10
16
26
Now we have a single root…This is the Huffman Tree!
4/21/2020 Huffman Coding 40

41. LetsAnalyzeHuffman Tree
• All characters are at the leaf nodes
• The number at the root = # of characters in the file
• High-frequency chars (E.g., “e”) are near the root
• Low-frequency chars are far from the root
E
☐
4
e
8
2 2
i y l k .
1 1 1 1 1 1
2
r s
2 2
4
n a
2 2
4
4
6
8
10
16
26
4/21/2020 Huffman Coding 41

42. LetsAssignCodes
• Traverse the tree
• Any left edge  add label 0
• As right edge add label 1
• The code for each character is its root-to-leaf label sequence
☐
4
e
8
2 2
E i y l k .
1 1 1 1 1 1
2
r s
4
n a
2 2 2 2
4
4
6
8
10
16
26
4/21/2020 Huffman Coding 42

43. • Traverse the tree
• Any left edge  add label 0
• As right edge  add label 1
• The code for each character is its root-to-leaf label sequence
☐
4
e
8
2 2
E i y l k .
1 1 1 1 1 1
2
r s
4
n a
2 2 2 2
4
4
6
8
10
16
26
0
1
0
0
0
0
0
0 0
1
1
11
1
1
1
10
01 0 1
4/21/2020 Huffman Coding 43
LetsAssignCodes

44. Char Code
E 0000
i 0001
y 0010
l 0011
k 0100
. 0101
space☐ 011
e 10
r 1100
s 1101
n 1110
a 1111
Coding Table
4/21/2020 Huffman Coding 44
• Traverse the tree
• Any left edge  add label 0
• As right edge  add label 1
• The code for each character is its root-to-leaf label sequence
LetsAssignCodes

45. Huffman Algorithm
4/21/2020 Huffman Coding 45
• Step 1: Get Frequencies
• Scan the file to be compressed and count the occurrence of
each character
• Sort the characters based on their frequency
• Step 2: Build Tree & Assign Codes
• Build a Huffman-code tree (binary tree)
• Traverse the tree to assign codes
• Step 3: Encode (Compress)
• Scan the file again and replace each character by its code
• Step 4: Decode (Decompress)
• Huffman tree is the key to decompress the file

46. 46
Poll Question#5 : In Huffman coding, data in a tree always occur?
A. Roots
B. Leaves
C. left sub trees
D. right sub trees
4/21/2020 Huffman Coding

47. Step3: Encode(Compress)The File
Eerie eyes seen near lake.
Input File: Char Code
E 0000
i 0001
y 0010
l 0011
k 0100
. 0101
space☐ 011
e 10
r 1100
s 1101
n 1110
a 1111
Coding Table
+
Generate the
encoded file
000010 1100 000110 ….
Notice that no code is prefix to any other code
Ensures the decoding will be unique (Unlike Slide13)
4/21/2020 Huffman Coding 47

48. Step4: Decode(Decompress)
• Must have the encoded file + the coding tree
• Scan the encoded file
• For each 0  move left in the tree
• For each 1  move right
• Until reach a leaf node  Emit that character and go back
to the root
4/21/2020 Huffman Coding 48

49. Huffman Coding4/21/2020 49
0000 10 1100 000110 ….
Eerie …
Generate the
original file
+

50. Huffman Algorithm
• Step 1: Get Frequencies
• Scan the file to be compressed and count the occurrence of
each character
• Sort the characters based on their frequency
• Step 2: Build Tree & Assign Codes
• Build a Huffman-code tree (binary tree)
• Traverse the tree to assign codes
• Step 3: Encode (Compress)
• Scan the file again and replace each character by its code
• Step 4: Decode (Decompress)
• Huffman tree is the key to decompess the file
4/21/2020 Huffman Coding 50

51. Pseudocode:HuffmanCoding
• An appropriate data structure is a binary min-heap
• Rebuilding the heap is lgn and n-1 extractions are made, so the
complexity is O( nlgn)
• The encoding is NOT unique, other encoding may work just as well,
but none will work better
4/21/2020 Huffman Coding 51

52. LabAssignment
• Example Input: Huffman coding is a data compression algorithm.
• Output:
4/21/2020 Huffman Coding 52

53. 4/21/2020 Huffman Coding 53