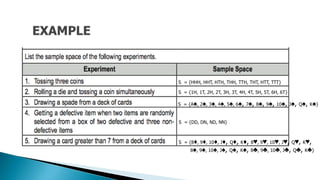
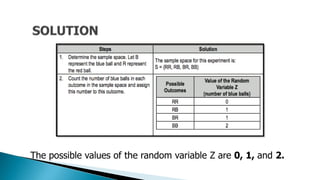
The document covers key concepts in statistics and probability, focusing on random variables which can be classified as discrete or continuous. It provides examples of sample spaces and the assignment of values to outcomes, illustrating how random variables function in different scenarios, such as tossing coins or drawing cards. The lesson concludes by distinguishing between discrete random variables, which have countable outcomes, and continuous random variables, which can take on an infinite range of values.

1. DOMINIC DALTON L. CALING
Statistics and Probability | Grade 11

2. At the end of this lesson, you are expected to:
• illustrate a random variable;
• classify random variables as discrete or
continuous; and
• find the possible values of a random variable.

3. The set of all possible outcomes of an experiment
and represented by the symbol S. It also refers as
the population.

4. S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
S = {1H, 1T, 2H, 2T, 3H, 3T, 4H, 4T, 5H, 5T, 6H, 6T}
S = {A♠, 2♠, 3♠, 4♠, 5♠, 6♠, 7♠, 8♠, 9♠, 10♠, J♠, Q♠, K♠}
S = {DD, DN, ND, NN}
S = {8♦, 9♦, 10♦, J♦, Q♦, K♦, 8♥, 9♥, 10♥, J♥, Q♥, K♥,
8♠, 9♠, 10♠, J♠, Q♠, K♠, 8♣, 9♣, 10♣, J♣, Q♣, K♣}

5. If three coins are tossed, what numbers can be assigned
for the frequency of heads that will occur?
If three cards are drawn from a deck, what number can
be assigned for the frequency of face cards that will
occur?
The answers to these questions require an
understanding of random variables.

6. Suppose three cell phones are tested at random. We want to
find out the number of defective cell phones that occur.
Thus, to each outcome in the sample space we shall assign
a value.
Sample Space
S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}

7. To each outcome in the sample space we shall assign a value.
0 - if there is no defective cell phone
1 - if there is 1 defective cell phone
2 - if there are two defective cell phones
3 - if there are three defective cell phones
The number of defective cell phones is a random variable.

8. The possible values of this random variable are 0, 1, 2, and 3.

9. A random variable is a function that associates
a real number to each element in the sample
space. It is a variable whose values are
determined by chance.

10. Tossing Three Coins
Suppose three coins are tossed. Let Y be the random variable
representing the number of tails that occur. Find the values of the
random variable Y. Complete the table below.

11. The possible values of this random variable are 0, 1, 2, and 3.

12. Drawing Balls from an Urn
Two balls are drawn in succession without replacement from an urn containing 5 red
balls and 6 blue balls. Let Z be the random variable representing the number of blue
balls. Find the values of the random variable Z. Complete the table below.

13. The possible values of the random variable Z are 0, 1, and 2.

14. If three coins are tossed, what numbers can be assigned
for the frequency of heads that will occur?
If three cards are drawn from a deck, what number can
be assigned for the frequency of face cards that will
occur?

15. A random variable is a discrete random variable if its set of possible
outcomes is countable. Mostly, discrete random variables represent count
data, such as the number of defective chairs produced in a factory.
For Example 1, the possible values of random variable Y are 0, 1, 2, and
3. The possible values for random variable Z in Example 2, are 0, 1, and
2. Random variables Y and Z are discrete random variables.

16. A random variable is a continuous random variable if it
takes on values on a continuous scale. Often, continuous
random variables represent measured data, such as heights,
weights, and temperatures.

17. Suppose an experiment is conducted to determine the distance
that a certain type of car will travel using 10 liters of gasoline
over a prescribed test course. If distance is a random variable,
then we have an infinite number of distances that cannot be
equated to the number of whole numbers. This is an example
of a continuous random variable.

18. Classify the following random variables as discrete or continuous.
1. the number of defective computers produced by a manufacturer
2. the weight of newborns each year in a hospital
3. the number of siblings in a family of a region
4. the amount of paint utilized in a building project
5. the number of dropout in a school district for a period of 10
years
discrete
discrete
discrete
continuous
continuous