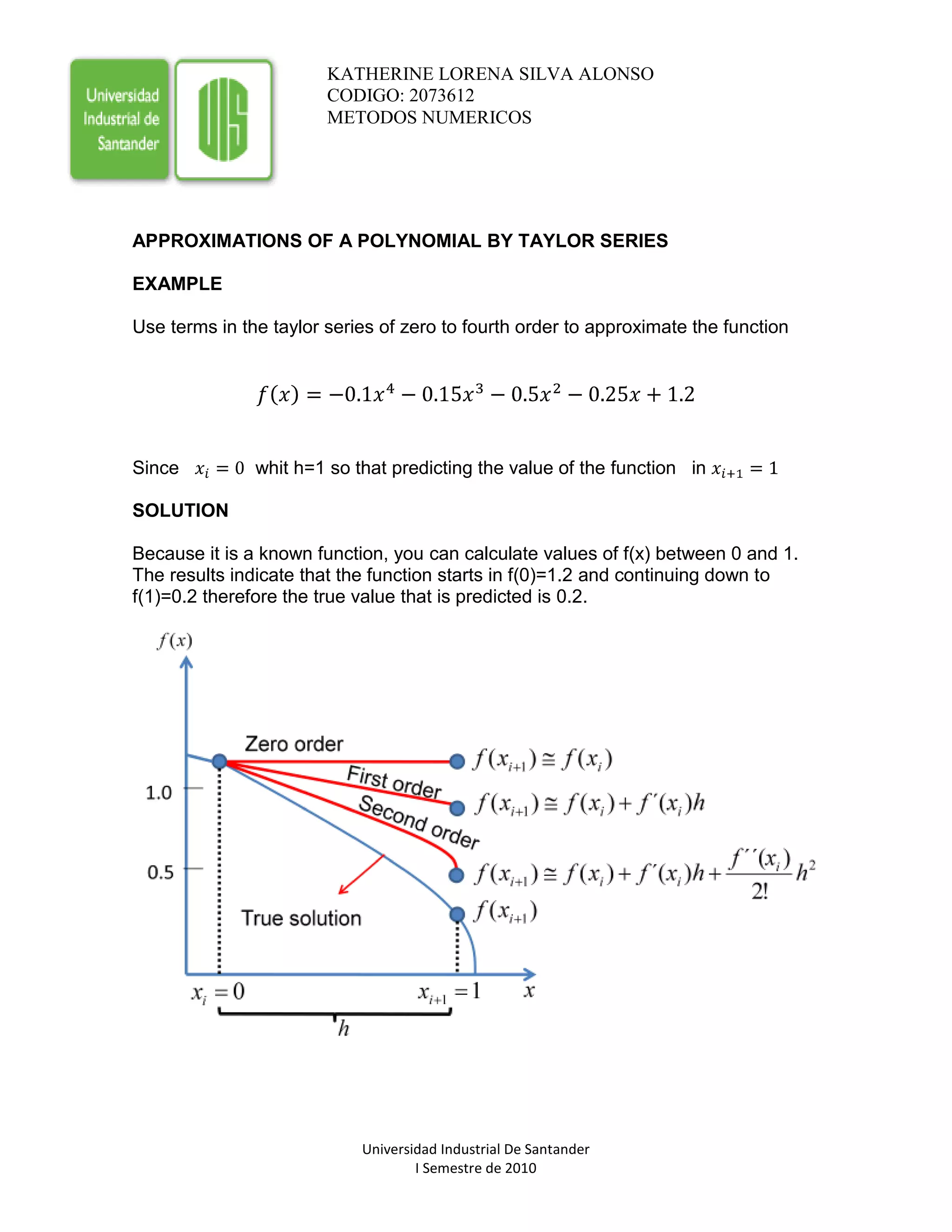
The document discusses using Taylor series approximations to estimate the value of a polynomial function f(x) at x=1. Specifically: 1) The zero-order approximation (constant term only) estimates f(1) as 1.2 with an error of -1.0. 2) The first-order approximation (linear term only) estimates f(1) as 0.95 with an error reduced to -0.75. 3) The second-order approximation (quadratic term added) estimates f(1) as 0.45, improving the estimate. Higher-order terms provide successively better approximations, with the fourth-order matching the true value of 0.2.

1. KATHERINE LORENA SILVA ALONSOCODIGO: 2073612METODOS NUMERICOS-534035-455295 <br />APPROXIMATIONS OF A POLYNOMIAL BY TAYLOR SERIES<br />EXAMPLE<br />Use terms in the taylor series of zero to fourth order to approximate the function<br />fx=-0.1x4-0.15x3-0.5x2-0.25x+1.2<br />Since xi=0 whit h=1 so that predicting the value of the function in xi+1=1<br />SOLUTION<br />Because it is a known function, you can calculate values of f(x) between 0 and 1. The results indicate that the function starts in f(0)=1.2 and continuing down to f(1)=0.2 therefore the true value that is predicted is 0.2.<br />True solution0.51.0Second orderFirst orderZeroorder<br />Approximations in the Taylor series with n = 0<br />f(xi+1)≅f(xi)<br />f(xi+1)≅0.2<br />As seen in the figure, the zero-order approximation is a constant by using this formulation is the truncation error of: <br />Er=0.2-1.2=-1.0<br />En x=1<br />For n=1 the first derivative must be determined and assess in x=0, like:<br />f´0=-0.40.03-0.450.02-1.00.0-0.25=-0.25<br />The first order approximation using the following equation<br />f(xi+1)≅fxi+f´xi(xi+1-xi)<br />f(xi+1)≅1.2-0.5h<br />That its can use for calculate f(1)= 0.95 so the approximation begins to coincide with the trajectory of the function as the slope of a straight line. Thus the truncation error is reduced to <br />Er=0.2-0.95=-0.75<br />For n=2 the second derivative must be determined in x=0<br />f´0=-1.20.03-0.90.02-1.0=-1.0<br />According to the following equation<br />f(xi+1)≅1.2-0.5h-0.5h2<br />Substituting h = 1, f (1) = 0.45. to include the second derivative is added to a downward curvature provides a best estimate as shown in Figure.<br />The additional terms improve the approximation. The inclusion of third and fourth derivative gives the same equation as a result of principle whit <br />f(xi+1)≅1.2-0.5h-0.5h2-0.15h3-0.1h4<br />Since the fifth derivative of a polynomial of fourth order is zero, then the expansion of Taylor series to the fourth derivative produces an accurate approximation in: <br />xi+1=1<br />f1≅1.2-0.51-0.51-0.1513-0.114=0.2<br />