1. CALCULATION OF THE ROOT
we first make the graph of the function to get an inkling of what the value of the root and so allocate an appropriate
x f(X)
0 1 GRAPH OF TH
0.1 0.71873075 1.2
0.2 0.47032005 1
0.3 0.24881164 0.8
0.4 0.04932896 0.6
0.5 -0.13212056 0.4
0.6 -0.29880579 0.2
0.7 -0.45340304 0
0.8 -0.59810348 -0.2 0 0.2
0.9 -0.73470111 -0.4
-0.6
-0.8
-1
we now make the evaluation of each of the methods
BISECTION METHOD
N° ITERATION Xi Xs Xr=Xi+Xs/2 F(Xi) F(Xr)
0 0 2 1 1 -0.86466472
1 0 1 0.5 1 -0.13212056
2 0 0.5 0.25 1 0.35653066
3 0.25 0.5 0.375 0.35653066 0.09736655
4 0.375 0.5 0.4375 0.09736655 -0.02063798
5 0.375 0.4375 0.40625 0.09736655 0.03749731
6 0.40625 0.4375 0.421875 0.03749731 0.00821964
7 0.421875 0.4375 0.4296875 0.00821964 -0.00626086
8 0.421875 0.4296875 0.42578125 0.00821964 0.00096637
9 0.42578125 0.4296875 0.427734375 0.00096637 -0.00265049
10 0.42578125 0.42773438 0.426757813 0.00096637 -0.00084287
11 0.42578125 0.42675781 0.426269531 0.00096637 6.1544E-05
FALSE POSITION METHOD
N° ITERACION Xi Xs Xr=Xs-F(Xs)(Xi-Xs)/F(Xi)-F(Xs) F(Xi) F(Xs)
0 0 2 0.67076181 1 -1.98168436
1 0 0.67076181 0.47594889 1 -0.40931479
2 0 0.47594889 0.436673946 1 -0.08994112
3 0 0.43667395 0.428480265 1 -0.01912266

2. 4 0 0.42848027 0.426760405 1 -0.00403004
5 0 0.4267604 0.426398958 1 -0.00084767
6 0 0.42639896 0.426322976 1 -0.00017823
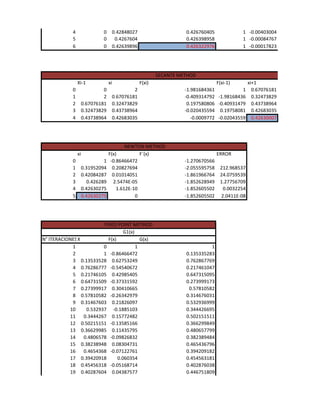
SECANTE METHOD
Xi-1 xi F(xi) F(xi-1) xi+1
0 0 2 -1.981684361 1 0.67076181
1 2 0.67076181 -0.409314792 -1.98168436 0.32473829
2 0.67076181 0.32473829 0.197580806 -0.40931479 0.43738964
3 0.32473829 0.43738964 -0.020435594 0.19758081 0.42683035
4 0.43738964 0.42683035 -0.0009772 -0.02043559 0.42630007
NEWTON METHOD
xi F(x) F´(x) ERROR
0 1 -0.86466472 -1.270670566
1 0.31952094 0.20827694 -2.055595758 212.968537
2 0.42084287 0.01014051 -1.861966764 24.0759539
3 0.426289 2.5474E-05 -1.852628949 1.27756709
4 0.42630275 1.612E-10 -1.852605502 0.0032254
5 0.42630275 0 -1.852605502 2.0411E-08
FIXED POINT METHOD
G1(x)
N° ITERACIONESX F(x) G(x)
1 0 1 1
2 1 -0.86466472 0.135335283
3 0.13533528 0.62753249 0.762867769
4 0.76286777 -0.54540672 0.217461047
5 0.21746105 0.42985405 0.647315095
6 0.64731509 -0.37331592 0.273999173
7 0.27399917 0.30410665 0.57810582
8 0.57810582 -0.26342979 0.314676031
9 0.31467603 0.21826097 0.532936999
10 0.532937 -0.1885103 0.344426695
11 0.3444267 0.15772482 0.502151511
12 0.50215151 -0.13585166 0.366299849
13 0.36629985 0.11435795 0.480657799
14 0.4806578 -0.09826832 0.382389484
15 0.38238948 0.08304731 0.465436796
16 0.4654368 -0.07122761 0.394209182
17 0.39420918 0.060354 0.454563181
18 0.45456318 -0.05168714 0.402876038
19 0.40287604 0.04387577 0.446751809

3. 20 0.44675181 -0.03753232 0.40921949
21 0.40921949 0.03190022 0.441119714
22 0.44111971 -0.02726464 0.413855074
23 0.41385507 0.02319384 0.437048918

4. ROOT
e root and so allocate an appropriate interval to assess
GRAPH OF THE FUNCTION
f(X)
0.4 0.6 0.8 1
F(Xi)*F(Xr) Ea
-0.86466472
-0.13212056 100
0.35653066 100
0.03471416 33.3333333
-0.00200945 14.2857143
0.00365098 7.69230769
0.00030821 3.7037037
-5.1462E-05 1.81818182
7.9432E-06 0.91743119
-2.5613E-06 0.456621
-8.1453E-07 0.22883295
5.9474E-08 0.11454754
THOD
F(Xr) F(Xi)*F(Xr) Ea
-0.40931479 -0.40931479
-0.08994112 -0.08994112 40.93147915
-0.01912266 -0.01912266 8.994111954
-0.00403004 -0.00403004 1.912265637

5. -0.00084767 -0.00084767 0.403003816
-0.00017823 -0.00017823 0.084767304
-3.7469E-05 -3.7469E-05 0.017822515
ERROR
198.168436
250
106.554579
25.7553761 200
2.47388323
0.12439283 150
100
50
0
0 2
-50

7. METODO SECANTE METODO NEWTON
% ERROR RELATIVO N° ITERACIONES % ERROR RELATIVO N° ITERACIONES
198.1684361 0 212.9685366 1
106.5545793 1 24.07595393 2
25.75537607 2 1.277567089 3
2.473883231 3 0.003225405 4
0.124392826 4 2.04108E-08 5

8. ERROR Vs ITERACIONES
METODO BISECCION
METODO SECANTE
METODO NEWTON
2 4 6 8 10 12

10. METODO BISECCION
N° ITERACIONES % ERROR RELATIVO
N° ITERACIONES
100 0
100 1
33.3333333 2
14.2857143 3
7.69230769 4
3.7037037 5

11. 1.81818182 6
0.91743119 7
0.456621 8
0.22883295 9
0.11454754 10