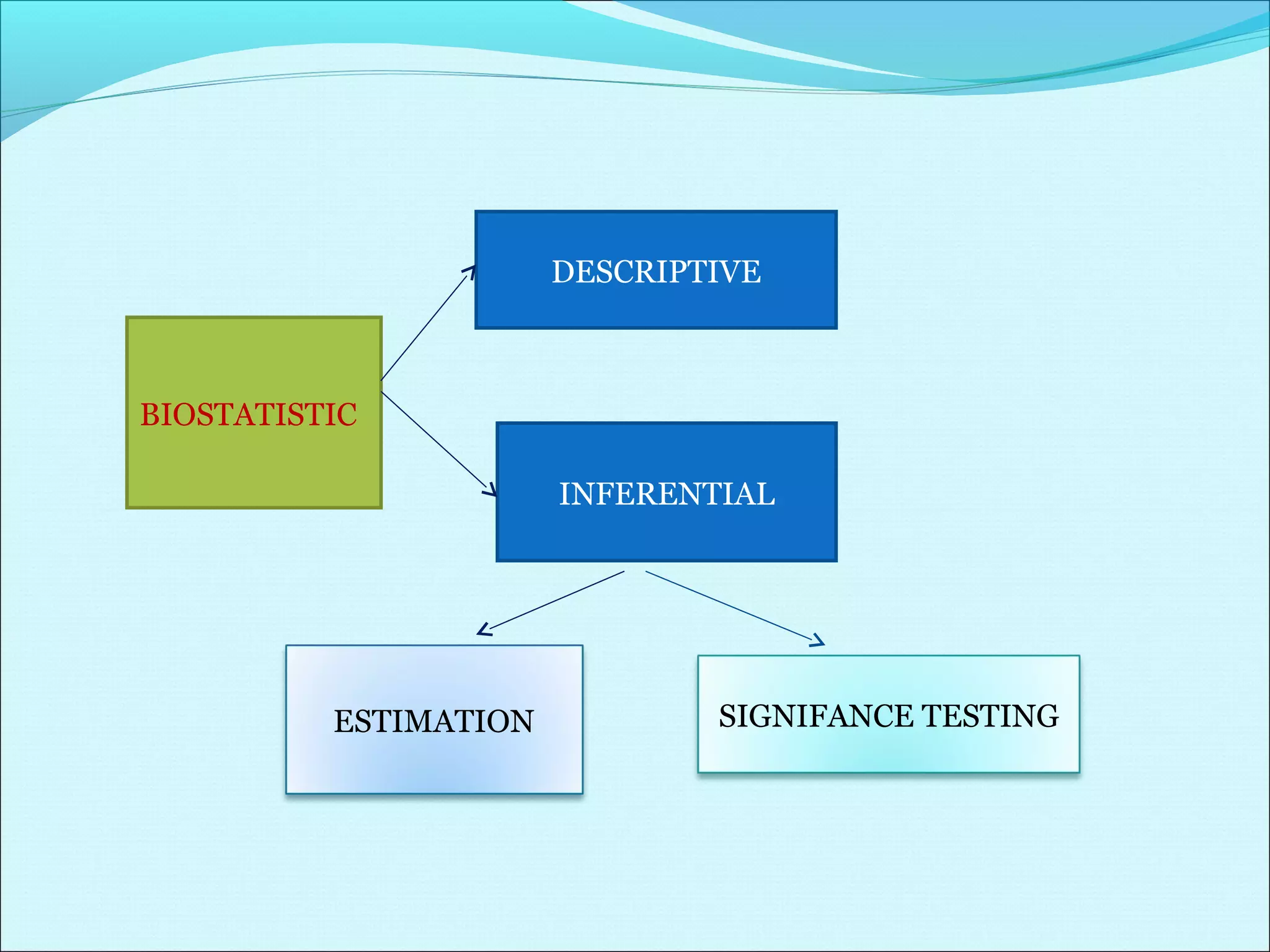
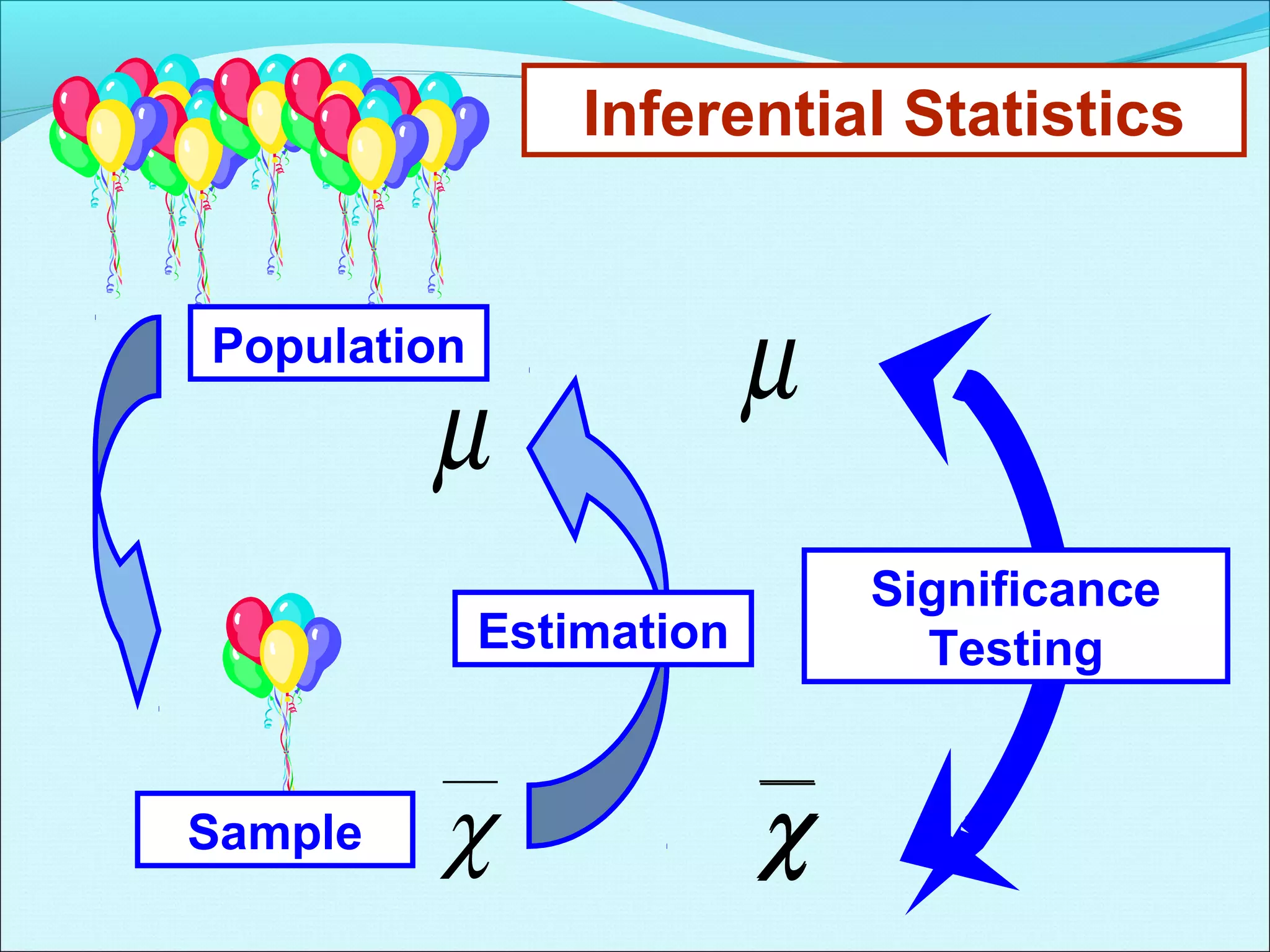
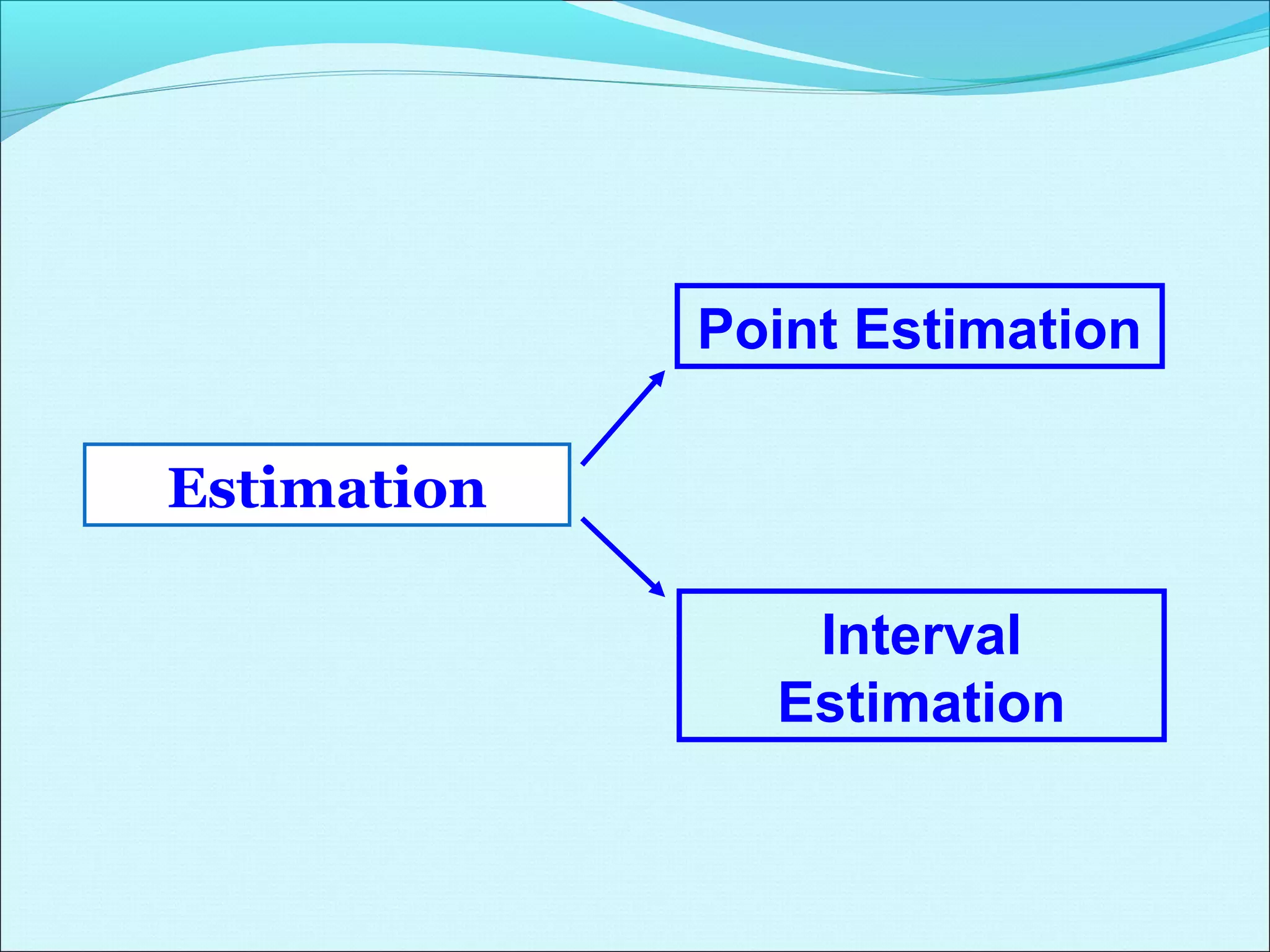
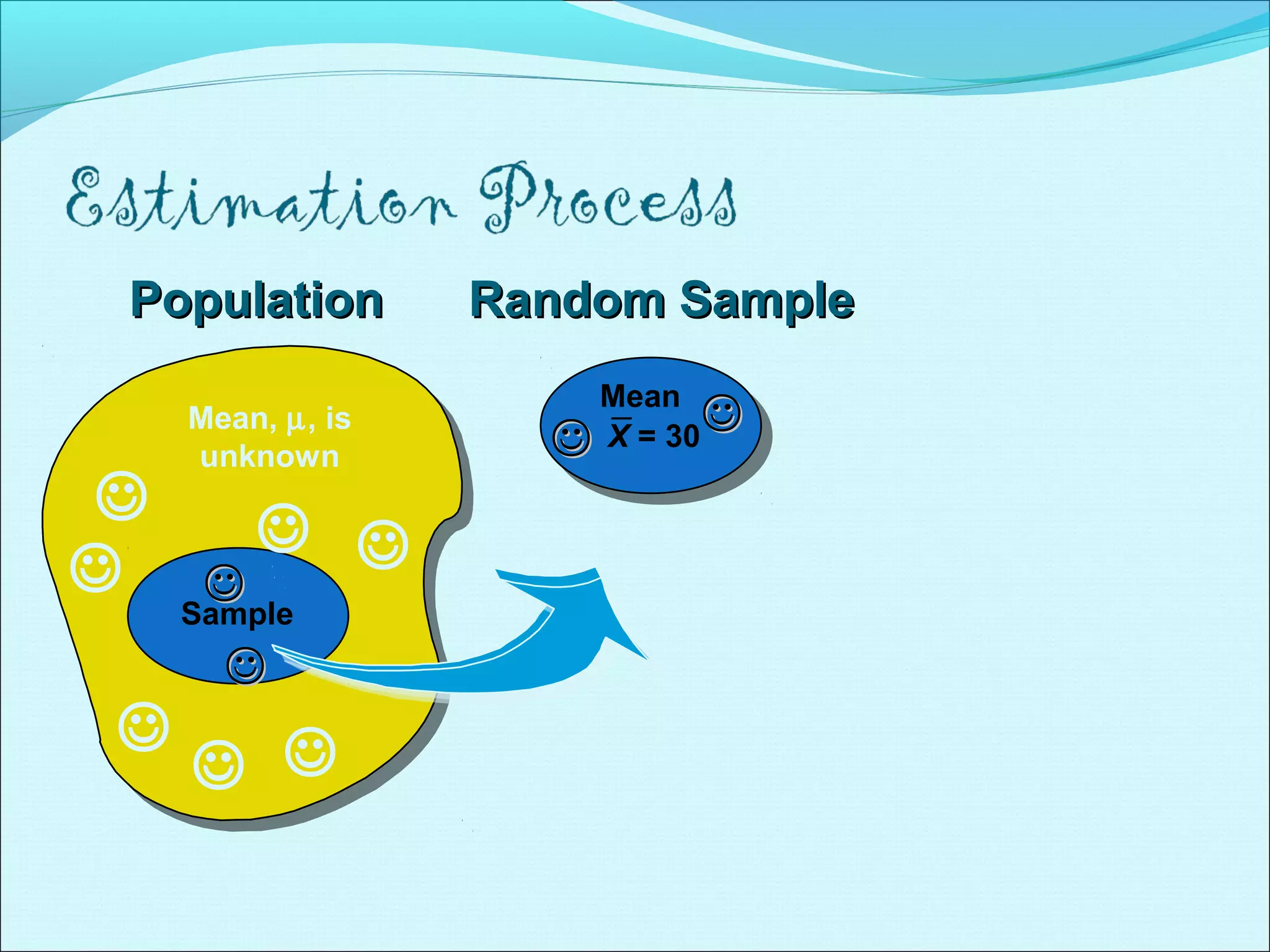
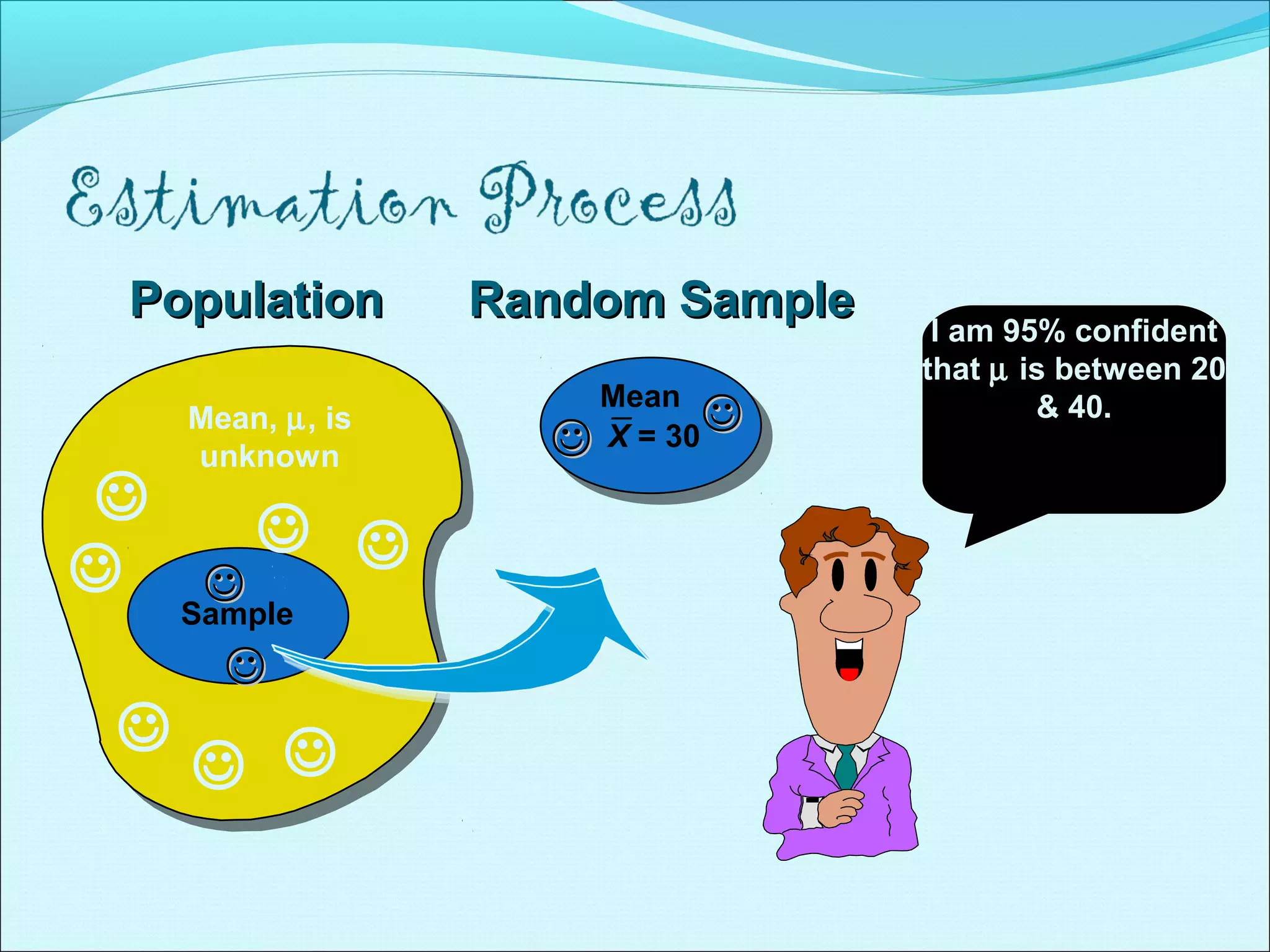
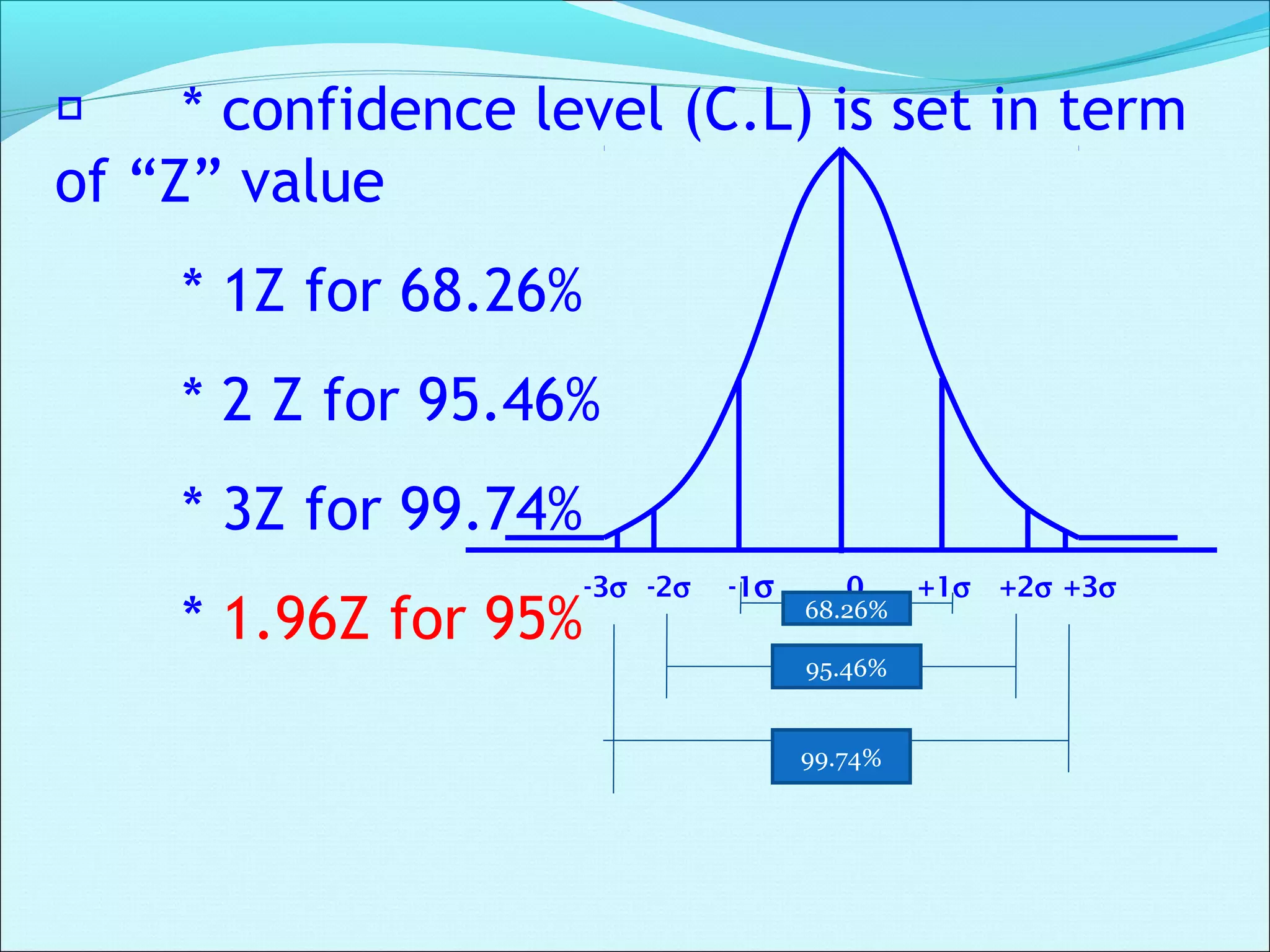
This document discusses statistical concepts related to descriptive and inferential statistics including estimation and significance testing. It explains point estimation and interval estimation. Point estimation provides a single value estimate of a population parameter based on a sample statistic. Interval estimation provides a range of plausible values for the population parameter with a stated probability based on a sample. The document provides examples of calculating confidence intervals and explains how confidence levels and sample sizes impact the width of confidence intervals.

1. Dr Su Su Khaing
Dr Htet Nu Wai

2. BIOSTATISTIC
DESCRIPTIVE
INFERENTIAL
ESTIMATION SIGNIFANCE TESTING

3. Sample
Population
χ
µ
Estimation
Inferential Statistics
χ
µ
Significance
Testing
χ

4. Estimation
Point Estimation
Interval
Estimation

5. Point estimation
• Once the sample has been drawn,
it has to be used to estimate
characteristics of the underlying
population.
• Calculating mean of a sample ( )
is a point estimation of sample
mean ( ) to population mean ( ).
χ
χ µ

6. Point Estimation
Provides single value
Based on observations from 1 sample
Gives no information about how close value is to the
unknown population parameter
Example: Sample meanX = 3 is point estimate of
unknown population mean

7. Interval Estimation
Provides range of values
Based on observations from 1 sample
Gives information about closeness to unknown
population parameter
Stated in terms of probability
Example: Unknown population mean lies between
50 & 70 with 95% confidence

8. Mean, µ, is
unknown
PopulationPopulation








9. Mean, µ, is
unknown
PopulationPopulation Random SampleRandom Sample
Mean
X = 30
Sample







 

10. Mean, µ, is
unknown
PopulationPopulation Random SampleRandom Sample
I am 95% confident
that µ is between 20
& 40.Mean
X = 30
Sample







 

11. Probabilistic Interpretation
Approximately 95% of intervals constructed in a
similar manner with samples of size n drawn from
the populations will contain the respective
population mean .

12. Practical Interpretation
We are 95% confident the population is between 20
and 40 .

13. Confidence interval (C.I)
Estimator ± ( reliability coefficient ) (standard error)
Estimator = mean, proportion
Reliability coefficient = confidence level
Confidence level is set in term of z or t value

14.  * confidence level (C.L) is set in term
of “Z” value
* 1Z for 68.26%
* 2 Z for 95.46%
* 3Z for 99.74%
* 1.96Z for 95%
-3σ -2σ -1σ 0 +1σ +2σ +3σ
68.26%
95.46%
99.74%

15. Confidence interval
Depend on
Confidence level &
 sample size
The larger the C.L, the larger the C.I
The larger the (n), the smaller the C.I

16. Calculation of CI
One mean
One proportion
Two Means
Two Proportions

17. Calculation of C.I
• one mean = – ±(C.L X S.E)
•One proportion = p ±(C.L X S.E)
χ