Downloaded 583 times
Uploaded byVrushali Nalawade
Problems on support reaction.pdf
The document provides solutions to multiple problems involving calculating support reactions for beams. The problems involve drawing free body diagrams of beams, then applying equations for the sum of forces and sum of moments at the supports to solve for the unknown support reactions. Key steps include considering the absence of any horizontal forces, setting equations for the sum of vertical forces and moments equal to zero, and solving the resulting systems of equations to find the support reactions.
More Related Content
Similar to Problems on support reaction.pdf
Problems on support reaction.pdf
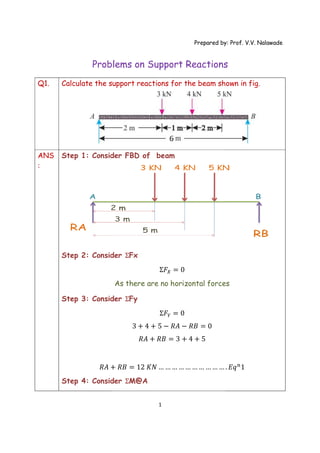
- 1. Problems on Q1. Calculatethe support reactions for the beam shown in fig ANS : Step 1: Consider Step 2: Consider Step 3: Consider 𝑅𝐴 + Step 4: Consider Prepared by: Prof. V.V. Nalawade 1 Problems on Support Reactions Calculate the support reactions for the beam shown in fig : Consider FBD of beam : Consider ƩFx Ʃ𝐹 = 0 As there are no horizontal forces : Consider ƩFy Ʃ𝐹 = 0 3 + 4 + 5 − 𝑅𝐴 − 𝑅𝐵 = 0 𝑅𝐴 + 𝑅𝐵 = 3 + 4 + 5 + 𝑅𝐵 = 12 𝐾𝑁 … … … … … … … … … … : Consider ƩM@A Prepared by: Prof. V.V. Nalawade Support Reactions Calculate the support reactions for the beam shown in fig. As there are no horizontal forces . 𝐸𝑞 1
- 2. (3 Put the valueof RB in Eq Step 5: Final Answer Reaction at support A = Reaction at support B = Q2. Calculate the support reactions for the beam shown in fig ANS : Step 1: Consider Step 2: Consider Prepared by: Prof. V.V. Nalawade 2 ƩM = 0 (3 × 2) + (4 × 3) + (5 × 5) − RB × 6 (3 × 2) + (4 × 3) + (5 × 5) = RB × RB × 6 = 6 + 12 + 25 RB = 43 6 = 7.17 KN Put the value of RB in Eqn 1, we get RA = 12-7.17 = 4.83 KN Final Answer Reaction at support A = RA = 4.83 KN Reaction at support B = RB = 7.17 KN Calculate the support reactions for the beam shown in fig : Consider FBD of beam : Consider ƩFx Prepared by: Prof. V.V. Nalawade = 0 6 4.83 KN RB = 7.17 KN Calculate the support reactions for the beam shown in fig.
- 3. Prepared by: Prof.V.V. Nalawade 3 Ʃ𝐹 = 0 As there are no horizontal forces Step 3: Consider ƩFy Ʃ𝐹 = 0 𝑅𝐴 + 𝑅𝐵 = 4 + (2 × 1.5) + 1.5 𝑅𝐴 + 𝑅𝐵 = 8.5 𝐾𝑁 … … … … … … … … … … . 𝐸𝑞 1 Step 4: Consider ƩM@A ƩM = 0 (4 × 1.5) + (3 × 2.25) + (1.5 × 4.5) = RB × 6 RB × 6 = 6 + 6.75 + 6.75 RB = 19.5 6 = 3.25 KN Put the value of RB in Eqn 1, we get RA = 8.5 – 3.25 = 5.25 KN Step 5: Final Answer Reaction at support A = RA = 5.25 KN Reaction at support B = RB = 3.25 KN Q3. A simply supported beam AB of Span 4.5 m is loaded as shown in fig. Find the support reactions at A & B.
- 4. ANS : Step 1: Consider Step2: Consider Step 3: Consider 𝑅𝐴 + Step 4: Consider Put the value of RB in Eq Step 5: Final Answer Reaction at support A = Reaction at support B = Prepared by: Prof. V.V. Nalawade 4 : Consider FBD of beam : Consider ƩFx Ʃ𝐹 = 0 As there are no horizontal forces : Consider ƩFy Ʃ𝐹 = 0 𝑅𝐴 + 𝑅𝐵 = 4.5 + 2.25 + 𝑅𝐵 = 6.75 𝐾𝑁 … … … … … … … … … … : Consider ƩM@A ƩM = 0 (4.5 × 2.25) + (2.25 × 3) = RB × 4. RB = 16.88 4.5 = 3.75 KN Put the value of RB in Eqn 1, we get RA = 6.75 – 3.75 = 3 KN Final Answer Reaction at support A = RA = 3 Reaction at support B = RB = 3.75 Prepared by: Prof. V.V. Nalawade there are no horizontal forces … . 𝐸𝑞 1 .5 KN 3.75 KN
- 5. Q4. Calculate thesupport reactions for the beam shown in fig ANS : Step 1: Consider Step 2: Consider As there are no horizontal Step 3: Consider 𝑉𝐴 + Step 4: Consider (120 × 3 Prepared by: Prof. V.V. Nalawade 5 Calculate the support reactions for the beam shown in fig : Consider FBD of beam : Consider ƩFx Ʃ𝐹 = 0 𝐻𝐴 = 0 As there are no horizontal forces acting on beam : Consider ƩFy Ʃ𝐹 = 0 𝑉𝐴 + 𝑅𝐵 = 120 + 30 + 90 + 𝑅𝐵 = 240 𝐾𝑁 … … … … … … … … … … : Consider ƩM@A ƩM = 0 3) + (30 × 6) + (40) + (90 × 8.67) = Prepared by: Prof. V.V. Nalawade Calculate the support reactions for the beam shown in fig. forces acting on beam … . 𝐸𝑞 1 ) = RB × 10
- 6. Put the valueof RB in Eq Step 5: Final Answer Horizontal Reaction at support A = H Vertical Reaction at support A = V Reaction at support B = Q5. Find analytically the support reactions at B and the load P, for the beam shown in fig. If the reaction of support A is Zero ANS : Step 1: Consider Step 2: Consider Prepared by: Prof. V.V. Nalawade 6 Put the value of RB in Eqn 1, we get VA = 240-136.03 = 103.97 KN Final Answer Horizontal Reaction at support A = H Vertical Reaction at support A = VA = 103.97 Reaction at support B = RB = 136.03 Find analytically the support reactions at B and the load P, for shown in fig. If the reaction of support A is Zero : Consider FBD of beam : Consider ƩFx Prepared by: Prof. V.V. Nalawade Horizontal Reaction at support A = HA = 0 103.97 KN 136.03 KN Find analytically the support reactions at B and the load P, for shown in fig. If the reaction of support A is Zero
- 7. Prepared by: Prof.V.V. Nalawade 7 Ʃ𝐹 = 0 𝐻𝐴 = 0 As there are no horizontal forces acting on beam Step 3: Consider ƩFy Ʃ𝐹 = 0 𝑉𝐴 + 𝑅𝐵 = 10 + 36 + 𝑃 0 + 𝑅𝐵 − 𝑃 = 46 𝐾𝑁 … … … … … … … … … … 𝑎𝑠 𝑉𝐴 = 0 𝑅𝐵 − 𝑃 = 46 𝐾𝑁 … … … … … … … … … … . 𝐸𝑞 1 Step 4: Consider ƩM@A ƩM = 0 (10 × 2) − 20 + (36 × 5) − (P × 7) = RB × 6 6RB − 7P = 220… … … … … … … … … … … … 𝐸𝑞 2 Solving Eqn 1 & 2, we get Putin Eqn 1, we get Step 5: Final Answer Reaction at support B = RB = 102 KN Load = P = 56 KN
- 8. Q6. Find thesupport reactions at A and B for the beam loaded as shown in fig. ANS : Step 1: Consider Step 2: Consider 𝐻𝐴 Step 3: Consider 𝑉𝐴 + 𝑅𝐵 Step 4: Consider Prepared by: Prof. V.V. Nalawade 8 Find the support reactions at A and B for the beam loaded as : Consider FBD of beam : Consider ƩFx Ʃ𝐹 = 0 𝐻𝐴 − 𝑅𝐵 𝐶𝑂𝑆 60 = 0 … … … … … … 𝐸𝑞 : Consider ƩFy Ʃ𝐹 = 0 𝑉𝐴 + 𝑅𝐵𝑠𝑖𝑛 60 = 120 + 90 + 80 𝑅𝐵 𝑠𝑖𝑛60 = 290 𝐾𝑁 … … … … … … … … … : Consider ƩM@A ƩM = 0 Prepared by: Prof. V.V. Nalawade Find the support reactions at A and B for the beam loaded as 𝐸𝑞 1 … … . 𝐸𝑞 2
- 9. (120 × Put inEqn 1 & 2 Step 5: Final Answer Horizontal Reaction at support A = H Vertical Reaction at support A = V Reaction at support B = Q7. Find the support reactions at A and F for the beam loaded as shown in fig. ANS : Step 1: Consider FBD of beam AC FBD of beam DF Prepared by: Prof. V.V. Nalawade 9 × 5) + (90 × 6) + (80 × 13) = RB sin & 2, we get Final Answer Horizontal Reaction at support A = HA = Vertical Reaction at support A = VA = Reaction at support B = RB = 251.72 Find the support reactions at A and F for the beam loaded as : Consider FBD of beam FBD of beam AC DF Prepared by: Prof. V.V. Nalawade sin60 × 10 A = 125.86 KN A = 72 KN 251.72 KN Find the support reactions at A and F for the beam loaded as
- 10. Consider FBD ofbeam DF first, Step 2: Consider Step 3: Consider 𝑉𝐹 Step 4: Consider Put in Eqn 1, we get Now Consider Step 5: Consider Prepared by: Prof. V.V. Nalawade 10 Consider FBD of beam DF first, : Consider ƩFx Ʃ𝐹 = 0 𝐻𝐹 = 0 : Consider ƩFy Ʃ𝐹 = 0 + 𝑅𝐷 = 120 … … … … … … … … … … . 𝐸𝑞 : Consider ƩM@D ƩM = 0 (120 × 3) − (VF × 4) = 0 1, we get Consider the FBD of beam AC, : Consider ƩFx Ʃ𝐹 = 0 𝐻𝐴 + 2 cos 59.04 = 0 Prepared by: Prof. V.V. Nalawade 𝐸𝑞 1
- 11. Prepared by: Prof.V.V. Nalawade 11 𝐻𝐴 = −1.03 𝐾𝑁 i.e. our assumed direction is wrong, Therefore 𝐻𝐴 = 1.03 𝐾𝑁 (←) Step 6: Consider ƩFy Ʃ𝐹 = 0 𝑉𝐴 − 𝑅𝐶 = 2 sin 59.04 𝑉𝐴 = 1.71 + 30 = 31.41 𝐾𝑁 (↑) Step 7: Consider ƩM@A −M − 2 sin 59.04 × 1 − (30 × 2) = 0 Step 8: Final Answer Horizontal Reaction at support A = HA = 1.03 KN Vertical Reaction at support A = VA = 31.41 KN Moment at support A = MA = 61.71 KN.m Horizontal Reaction at support F = HF = 0 KN Vertical Reaction at support F = VF = 90 KN Reaction at support D = RD = 30 KN Q8. Two beams AB & CD are arranged as shown in fig. Find the support reactions at D.
- 12. ANS : Step 1: Consider FBDof beam AB FBD of beam Prepared by: Prof. V.V. Nalawade 12 : Consider FBD of beam FBD of beam AB FBD of beam CD Prepared by: Prof. V.V. Nalawade
- 13. Step 2: Consider ( Step3: Consider Prepared by: Prof. V.V. Nalawade 13 : Consider FBD of AB & Consider ƩM@A ƩM = 0 (600 × 4) + 2400 = RB sin 53.13 × 12 Consider FBD of CD & Consider ƩM@C ƩM = 0 RD sin 36.87 × 10 − 500 × 4.2 = 0 Prepared by: Prof. V.V. Nalawade M@A 12 M@C 0
- 14. Q9. Prepared by: Prof.V.V. Nalawade 14 Prepared by: Prof. V.V. Nalawade
- 15. Prepared by: Prof.V.V. Nalawade 15 Q10. Q11.