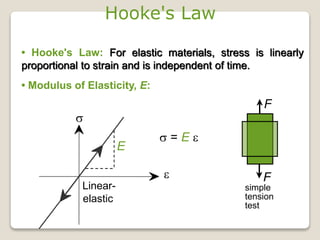
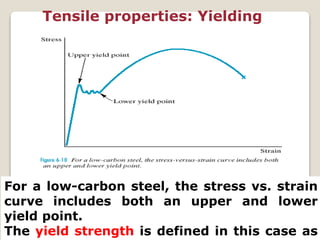
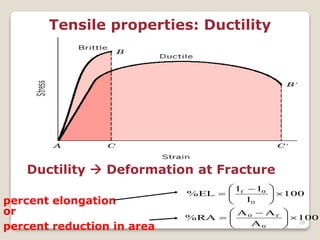
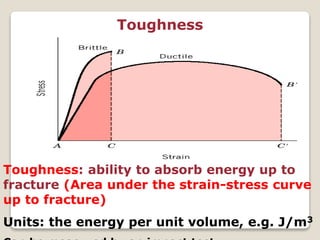
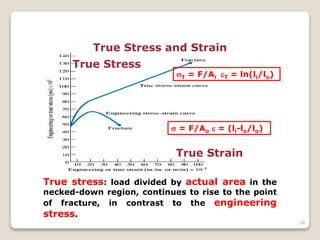
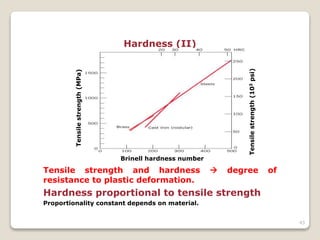
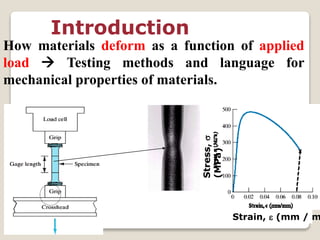
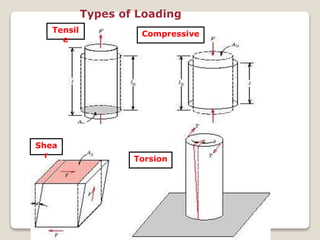
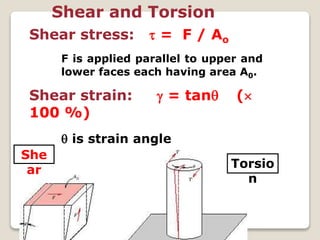
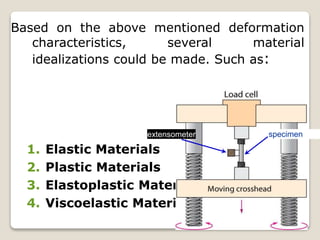
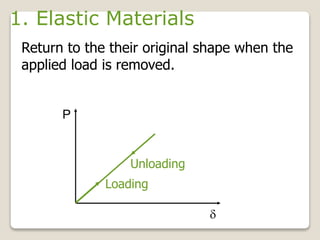
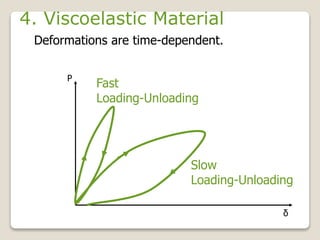
This document discusses the mechanical properties of materials. It defines mechanical properties as how materials behave when subjected to stresses and strains from applied forces. It explains different types of loading like tension, compression, and shear that materials can experience. It also defines concepts like stress, strain, elastic deformation, plastic deformation, and viscous deformation. Different material behaviors are described like elastic, plastic, elastoplastic, and viscoelastic. The document also discusses properties such as modulus of elasticity, Poisson's ratio, yield strength, ductility, toughness, resilience, hardness, and factors of safety in material design. Testing methods for mechanical properties and examples of stress-strain curves are provided.

1. MECHANICAL
PROPERTIES OF
MATERIALS
By Leliso H.

2. Cont…
Engineers are primarily concerned with the development
and design of machines, structures etc.
These products are often subjected to forces/
deformations, resulting in stresses/strains, the properties
of materials under the action of forces and deformations
becomes an important engineering consideration.
The properties of materials when subjected to stresses
and strains are called “mechanical properties”. In other
words the properties that determine the behavior of
engineering materials under applied forces are called
“mechanical properties”.

3. How materials deform as a function of applied
load  Testing methods and language for
mechanical properties of materials.
Introduction
Stress,
(MPa) Strain,  (mm / m

4. CONCEPTS OF STRESS AND STRAIN
If a load is static or changes relatively slowly
with time and is applied uniformly over a
cross section or surface of a member, the
mechanical behavior may be ascertained by a
simple stress–strain test; these are most
commonly conducted for metals at room
temperature.
There are three principal ways in which a load
may be applied: namely, tension,
compression, and shear

5. Types of Loading
Tensil
e
Compressive
Shea
r Torsion

6. Stress
(For Tension and Compression)
To compare specimens , the load is
calculated per unit area.
Engineering Stress:  = F / Ao
F: is load
A0: cross-sectional area
A0 perpendicular to F before
application of the load.

7. Strain
(For Tension and Compression)
Engineering Strain:  = l / lo
( 100 %)
l: change in length
lo: original length.
li instantaneous length.
Stress / strain = / 

8. Shear and Torsion
Shear stress:  = F / Ao
F is applied parallel to upper and
lower faces each having area A0.
Shear strain:  = tan (
100 %)
 is strain angle
She
ar Torsio
n

9.  Torsion is a variation of pure shear,
wherein a structural member is twisted.
Torsional forces produce a rotational
motion about the longitudinal axis of one
end of the member relative to the other
end.
 Examples of torsion are found for
machine axles and drive shafts, and also
for twist drills.
 Torsional tests are normally performed on
cylindrical solid shafts or tubes.
 A shear stress is a function of the applied
torque T, whereas shear strain is related
to the angle of twist,

10. Contd.
 The response of a material to applied forces depends
on the type and nature of the bond and the structural
arrangement of atoms, molecules or ions.
 Basic deformation types for load carrying materials
are:
1. Elastic deformation (deformations are instantaneously
recoverable)
2. Plastic deformation (non-recoverable)
3. Viscous deformation (time dependent deformation)

11. Viscous Deformation
• Plastic deformations in noncrystalline
solids (as well as liquids) occurs by a
viscous flow mechanism. Usually
attributed to fluids. But solids may
also behave like viscous materials
under high temperature and pressure.
• Viscous materials deform steadily
under stress.
• Deformations are time dependent.

12. Based on the above mentioned deformation
characteristics, several material
idealizations could be made. Such as:
1. Elastic Materials
2. Plastic Materials
3. Elastoplastic Materials
4. Viscoelastic Materials
specimenextensometer

13. 1. Elastic Materials
Return to the their original shape when the
applied load is removed.
Unloading
d
P
Loading

14. 2. Plastic Materials
No deformation is observed up to a certain limit.
Once the load passes this limit, permanent
deformartions are observed.
δ
P
Limit
Plastic deformation
Unloading
Loading

15. 3. Elastoplastic Materials
• Up to a limit shows elastic properties. Within this
limit if the load is removed, returns to its original
shape.
• If the load passes the limit, plastic deformations are
observed.
Plastic
deformation
Elastic
deformation
P
δ
Elastic
Limit

16. 4. Viscoelastic Material
Deformations are time-dependent.
P
δ
Slow
Loading-Unloading
Fast
Loading-Unloading

17. ISOTROPIC
and
ANISTROPIC
Materials

18. • The physical properties of some
substances depend on the
crystallographic direction in which the
measurements are taken.
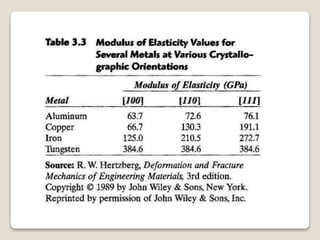
• For example, the elastic modulus, the
electrical conductivity, and index of
refraction may have different values in
the [100] and [111] directions.
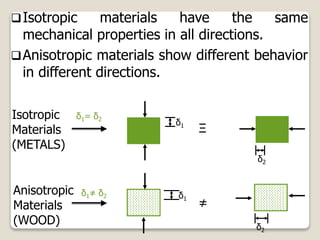
• This directionality of properties is
termed as anisotropy, and it is
associated with the variance of atomic
or ionic spacing with crystallographic
direction.
• Substances in which the measured

20. Isotropic materials have the same
mechanical properties in all directions.
Anisotropic materials show different behavior
in different directions.
Isotropic
Materials
(METALS)
Ξ
δ1
δ2
Anisotropic
Materials
(WOOD)
δ1
≠
δ2
δ1= δ2
δ1≠ δ2

21. Hooke's Law
• Modulus of Elasticity, E:
• Hooke's Law: For elastic materials, stress is linearly
proportional to strain and is independent of time.
 = E 

Linear-
elastic
E

F
F
simple
tension
test

22. Poisson’s ratio
Tension  shrink laterally
Compression  bulge.
Ratio of lateral to axial strain
called
Poisson's ratio .
Unloaded Loaded

23. Poisson’s ratio
z
y
z
x






 is dimensionless.
Sign:
• lateral strain opposite to
longitudinal strain
Theoretical value:
• For isotropic material: 0.25
• Maximum value: 0.50,
• Typical value: 0.24 - 0.30

24. Elastic Modulus, Poisson’s
Ratio
and
Shear Modulus
For isotropic material:
E = 2G(1+)  G ~ 0.4E
Single crystals are usually
elastically anisotropic
Elastic behavior varies with
crystallographic direction.

25. Plastic deformation
(Tension)
Plastic deformation:
• stress not proportional to strain
• deformation is not reversible
• deformation occurs by breaking and re-
arrangement of atomic bonds (crystalline
materials by motion of defects)

26. Tensile properties: YieldingStress
Strain
Yield strength: y , Permanent
strain= 0.002
Yield point: P
Where strain deviates from
being proportional to
stress
(the proportional limit)
A measure of resistance to
plastic deformation
P
y
0.002

27. Tensile properties: Yielding
For a low-carbon steel, the stress vs. strain
curve includes both an upper and lower
yield point.
The yield strength is defined in this case as

28. 28
Tensile properties: Ductility
percent elongation
or
percent reduction in area
Ductility  Deformation at Fracture
100
l
ll
EL%
0
0f





 

100
A
AA
RA%
0
f0





 


29. 29
Mechanical Properties of Metals
Yield strength and tensile strength vary
with thermal and mechanical treatment,
impurity levels, etc.
Variability related to behavior of
dislocations (Elastic moduli are relatively
insensitive)
Yield and tensile strengths and modulus of
elasticity: Decrease with increasing

30. 30
Toughness
Toughness: ability to absorb energy up to
fracture (Area under the strain-stress curve
up to fracture)
Units: the energy per unit volume, e.g. J/m3

31. Anelasticity
 Up to this point, it has been
assumed that elastic deformation is
time independent— that is, that an
applied stress produces an
instantaneous elastic strain that
remains constant over the period of
time the stress is maintained.
 It has also been assumed that upon
release of the load the strain is
totally recovered—that is, that the
strain immediately returns to zero.

32. Example Problem

34. Contd..,

35. Resilience
 Resilience is the capacity of a material to absorb
energy when it is deformed elastically and then,
upon unloading, to have this energy recovered.
 The associated property is the modulus of resilience, Ur
which is the strain energy per unit volume required to
stress a material from an unloaded state up to the point
of yielding.

36. Contd..,
 Assuming a linear elastic region

37. Toughness
 Toughness, it is a measure of the ability of a material
to absorb energy up to fracture.
 Specimen geometry as well as the manner of load
application are important in toughness determinations.
 For dynamic (high strain rate) loading conditions and
when a notch (or point of stress concentration) is
present, notch toughness is assessed by using an
impact test.
 Furthermore, fracture toughness is a property indicative
of a material’s resistance to fracture when a crack is
present

38. 38
True Stress and Strain
True stress: load divided by actual area in the
necked-down region, continues to rise to the point
of fracture, in contrast to the engineering
stress.
 = F/Ao  = (li-lo/lo)
T = F/Ai T = ln(li/lo)
True Strain
True Stress

39. 39
Elastic Recovery During Plastic Deformation
Deformed plastically, stress released, material has permanent
strain.
If stress is reapplied, material again responds elastically at
the beginning up to a new yield point that is higher than the
original yield point.
Elastic strain before reaching the yield point is called elastic
strain recovery.
y
y

40. Problems based on Ductility
and True-Stress-At-Fracture

42. 42
Hardness (I)
Hardness measure of material’s resistance
to localized plastic deformation
(e.g. dent or scratch)
Moh’s scale  ability of a material to scratch
another material: from 1 (softest = talc) to 10
(hardest = diamond).Variety of hardness tests
(Rockwell, Brinell, Vickers, etc.).
Small indenter (sphere, cone, or
pyramid) forced into surface of
material under controlled
magnitude and rate of loading.
Depth or size of indentation is
measured.
Tests are approximate, but
popular because they are easy
and non-destructive (except for
the small dent).

43. 43
Hardness (II)
Tensile strength and hardness  degree of
resistance to plastic deformation.
Hardness proportional to tensile strength
Proportionality constant depends on material.
Tensilestrength(MPa)
Tensilestrength(103psi)
Brinell hardness number

44. 44
What are the limits of “safe” deformation?
Design stress:
d = N’c : c = maximum anticipated stress,
N’ the “design factor” > 1.
Make sure d < y, safe or working stress:
w = y/N where N is “factor of safety” > 1.
For practical engineering design, the
yield strength is usually the
important parameter
Strain
Stress