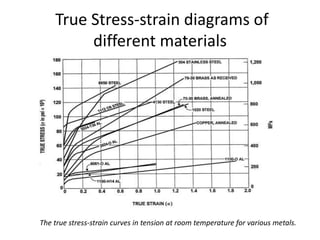
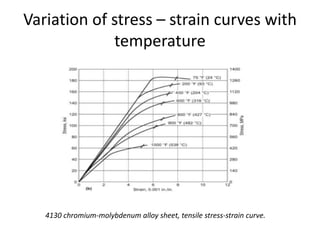
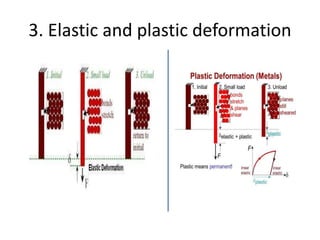
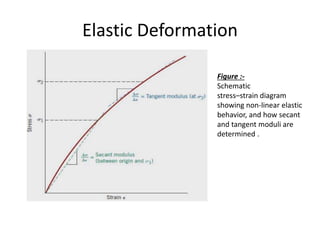
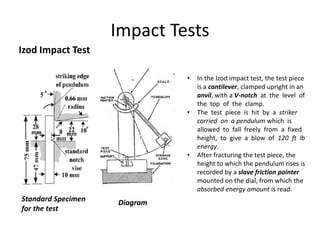
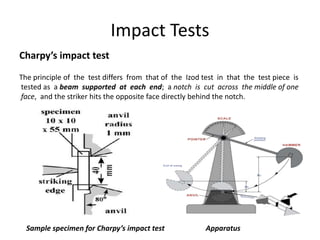
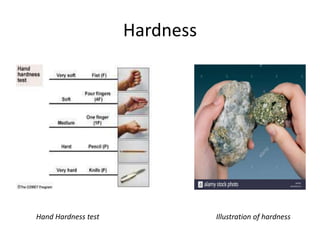
Mechanical properties refer to how materials behave under forces or pressures. This document discusses key mechanical properties including brittleness, hardness, strength, stiffness, ductility, malleability, elasticity, plasticity, creep, and weldability. It describes how these properties are defined, measured, and their significance for material selection and design. Measurement techniques covered include indentation hardness tests like Rockwell and Brinell, and tension tests. The document also examines stress-strain diagrams and how they vary for different materials and temperatures.

1. MECHANICAL PROPERTIES OF
MATERIALS
BME UG-II
SECTION - B1
GROUP - I
JADAVPUR UNIVERSITY

2. What do we mean by mechanical
properties of any material ?
Characteristics that indicate the elastic or
inelastic behavior of a material under pressure
(force), such as bending, brittleness, elongation,
hardness, tensile strength and so on are known
as mechanical properties .

3. Why do we need to know about the
mechanical properties of a material ?
1. To be able to select a material for a given use
based on considerations of cost and
performance .
2. To understand the loading limits of materials
and the change of their properties with use
3. To be able to create a new material that will
have solved the problems associated with
previously used materials.

4. Topics
• 1. Types and definitions of different
mechanical properties
• 2. Types of stress – strain diagrams
• 3. Elastic and plastic deformations
• 4. Measurement of mechanical properties

5. 1. Types and definitions of different
mechanical properties

6. Brittleness
1. A material is brittle if, when subjected to stress,
it breaks without significant deformation (strain).
2. Brittle materials absorb relatively little energy
prior to fracture, even those of high strength.
Breaking is often accompanied by a snapping
sound.
3. Brittle materials include most ceramics and
glasses (which do not deform plastically) and
some polymers, such as PMMA and polystyrene

7. Brittleness
Brittle fracture in cast iron
tensile testpieces
Illustration of brittleness

8. Hardness
• Hardness is a measure of how resistant solid matter is
to various kinds of permanent shape change when a
compressive force is applied.
• Some materials (e.g. metals) are harder than others
(e.g. plastics). Macroscopic hardness is generally
characterized by strong intermolecular bonds, but the
behavior of solid materials under force is complex;
therefore, there are different measurements of
hardness: scratch hardness, indentation hardness,
and rebound hardness.

9. Hardness
Hand Hardness test Illustration of hardness

10. Malleability
• Malleability is a substance's ability to deform under pressure
(compressive stress). If malleable, a material may be flattened into thin
sheets by hammering or rolling.
• Malleability is a physical property of matter, usually metals. It usually
applies to the family groups 1 to 12 on the modern periodic table of
elements. It is the ability of a solid to bend or be hammered into other
shapes without breaking.
• Examples of malleable metals are gold, iron, aluminum, copper, silver,
and lead.
• Gold and silver are highly malleable. When a piece of hot iron is
hammered it takes the shape of a sheet. The property is not seen in non-
metals. Non-malleable metals may break apart when struck by a hammer.
Malleable metals usually bend and twist in various shapes.

11. Malleability
Aluminium plates Gold bars
Aluminium and gold are examples of malleable materials.

12. Ductility
• In materials science, ductility is a solid
material's ability to deform
under tensile stress; this is often characterized
by the material's ability to be stretched into a
wire.

13. Ductility
Applications of ductile materials

14. Plasticity
• In physics and engineering, plasticity is the
propensity of a material to undergo
permanent deformation under load.
• The characteristics of material by which it
undergoes inelastic strain beyond those at the
elastic limit is known as plasticity .

15. Plasticity
Elastic and plastic regions of a material in stress – strain plot

16. Elasticity
• Elasticity refers to the material's ability to deform in
a non-permanent way, meaning that when the stress
load is removed from the material it will recover its
original form.
• A material will continue to deform elastically as the
stress upon it increases until the elastic limit is
reached.

17. Elasticity
Explanation of elasticity

18. Strength
• In materials science, the strength of a material is its
ability to withstand an applied load without failure or
plastic deformation.
• The field of strength of materials deals with forces and
deformations that result from their acting on a
material.
• A load applied to a mechanical member will induce
internal forces within the member called stresses when
those forces are expressed on a unit basis.

19. Categories of strength
• Yield strength is the lowest stress that produces a permanent deformation in a
material. In some materials, like aluminium alloys, the point of yielding is difficult
to identify, thus it is usually defined as the stress required to cause 0.2% plastic
strain. This is called a 0.2% proof stress.
• Compressive strength is a limit state of compressive stress that leads to failure in a
material in the manner of ductile failure (infinite theoretical yield) or brittle failure
(rupture as the result of crack propagation, or sliding along a weak plane -
see shear strength).
• Tensile strength or ultimate tensile strength is a limit state of tensile stress that
leads to tensile failure in the manner of ductile failure (yield as the first stage of
that failure, some hardening in the second stage and breakage after a possible
"neck" formation) or brittle failure (sudden breaking in two or more pieces at a
low stress state).
• Fatigue strength is a measure of the strength of a material or a component under
cyclic loading, and is usually more difficult to assess than the static strength
measures. Fatigue strength is quoted as stress amplitude or stress range, usually at
zero mean stress, along with the number of cycles to failure under that condition
of stress.
• Impact strength, is the capability of the material to withstand a suddenly applied
load and is expressed in terms of energy. Often measured with the Izod impact
strength test or Charpy impact test, both of which measure the impact energy
required to fracture a sample.

20. Strength
Applications of strength of materials

21. Stiffness
• Stiffness is the rigidity of an object — the
extent to which it resists deformation in
response to an applied force.
• The complementary concept is flexibility or
pliability: the more flexible an object is, the
less stiff it is.

22. Stiffness
• The stiffness, k, of a body is a measure of the resistance offered by
an elastic body to deformation. For an elastic body with a
single degree of freedom (DOF) (for example, stretching or
compression of a rod), the stiffness is defined as
k=F/δ
where :
• F is the force applied on the body
• δ is the displacement produced by the force along the same degree
of freedom (for instance, the change in length of a stretched spring)

23. Stiffness
• A body may also have a rotational stiffness, k,
given by
k=M/θ
• M is the applied moment
• θ is the rotation

24. A particular case of stiffness

25. Weldability
• The weldability, also known as joinability,[1] of a
material refers to its ability to be welded.
• Many metals and thermoplastics can be welded,
but some are easier to weld than others .
• A material's weldability is used to determine the
welding process and to compare the final weld
quality to other materials.

26. Weldability
Weldability helps choosing a material for welding purposes

27. Castability
• Castability (Fluidity) is the ability of the molten
metal to flow easily without premature
solidification is a major factor in determining the
proper filling of the mold cavity.
• The higher the castability of a molten metal, the
easier it is for that molten metal to fill thin
grooves in the mold and exactly reproduce shape
of mold cavity, there by successfully producing
the castings with thinner sections.

28. Castability
3- sand moulds at a foundry shop
Applications of castability

29. Creep
• In materials science, creep (sometimes called cold
flow) is the tendency of a solid material to move slowly
or deform permanently under the influence of
mechanical stresses.
• It can occur as a result of long-term exposure to high
levels of stress that are still below the yield strength of
the material.
• Creep is more severe in materials that are subjected
to heat for long periods, and generally increases as
they near theirmelting point.

30. Creep
Typical creep curve for engineering materials

31. 2. Types of stress-strain diagrams

32. Stress
(For Tension and Compression)
• To compare specimens , the load is calculated per unit
area.
• Stress:  = F / Ao
• F: is load
• A0: cross-sectional area
• A0 perpendicular to F before application of the load.

33. Strain
(For Tension and Compression)
• Strain:  = l / lo ( 100 %)
• l: change in length
• lo: original length.
• Stress / strain = / 

34. True stress and strain
T = F/Ai T = ln(li/lo)
= F/Ao  = (li-lo/lo)
True Strain
True Stress
True stress: load divided by actual area
in the necked-down region, continues to rise
to the point of fracture, in contrast to the
engineering stress.
True strain is the deformation divided by the
actual deformed length (the length changing
with respect to time) of the specimen at that
load. Engineering strain is the amount that a
material deforms per unit length in a tensile
test.

35. Stress – strain diagrams
Important points on a stress – strain diagram in general

36. Stress-Strain Behavior
(Tension)
Elastic deformation
Reversible:
( For small strains)
Stress removed  material returns to original
size
Plastic deformation
Irreversible:
Stress removed  material does not return to
original dimensions.

37. Conventional stress-strain
diagram
• Figure shows the characteristic stress-strain
diagram for steel, a commonly used material for
structural members and mechanical elements

38. Conventional stress-strain
diagram
Strain hardening.
• Ultimate stress, σu
• While specimen is elongating, its x-sectional area will decrease
• Decrease in area is fairly uniform over entire gauge length

39. Conventional stress-strain
diagram
Necking.
• At ultimate stress, x-sectional area begins to decrease in a localized region
• As a result, a constriction or “neck” tends to form in this region as
specimen elongates further
• Specimen finally breaks at fracture stress, σf

40. Conventional stress-strain
diagram
Fracture:
Specimen finally breaks at fracture stress, σf

41. Stress-strain diagrams of different
materials
Schematic of the different types of stress strain curves in a polymer

42. Stress-strain diagrams of different
materials
Stress- strain diagram for various types of steel

43. Stress-strain diagrams of different
materials
Comparative study of the stress – strain diagrams of brittle and ductile materials

44. Stress-strain diagrams of different
materials
Stress-strain diagram on basis of strong and tough

45. Stress-strain diagrams of different
materials
Explanation of regions in a stress – strain diagram for different materials

46. True Stress-strain diagrams of
different materials
The true stress-strain curves in tension at room temperature for various metals.

47. Variation of stress – strain curves with
temperature
4130 chromium-molybdenum alloy sheet, tensile stress-strain curve.

48. Deformation
In materials science, deformation refers to any changes in the shape or
size of an object due to-
1. An applied force (the deformation energy in this case is transferred
through work) or
2. A change in temperature (the deformation energy in this case is
transferred through heat).
The first case can be a result of tensile (pulling) forces, compressive (pushing)
forces, shear, bending or torsion (twisting).
In the second case, the most significant factor, which is determined by the
temperature, is the mobility of the structural defects such as grain
boundaries, point vacancies, line and screw dislocations, stacking faults and
twins in both crystalline and non-crystalline solids.

49. 3. Elastic and plastic deformation

50. Elastic Deformation
The degree to which a structure deforms or strains depends on the magnitude
of an imposed stress. For most metals that are stressed in tension and at
relatively low levels, stress and strain are proportional to each other through the
relationship :-
This is known as Hooke’s law, and the constant of proportionality E (GPa or psi)6
is the modulus of elasticity, or Young’s modulus. For most typical metals the magnitude
of this modulus ranges between 45 GPa ( psi), for magnesium, and
407 GPa ( psi), for tungsten .

51. Elastic Deformation
Figure :-
Schematic stress–strain diagram showing linear
elastic deformation for loading and unloading
cycles.
For elastic deformation , application of the load corresponds to moving from the
origin up and along the straight line. Upon release of the load, the same line is
traversed in the opposite direction, back to the origin .

52. Elastic Deformation
Figure :-
Schematic
stress–strain diagram
showing non-linear elastic
behavior, and how secant
and tangent moduli are
determined .

53. Elastic Deformation
Figure :-
Force (F)
versus interatomic
separation (r) for
weakly and strongly
bonded atoms
The magnitude of the modulus of elasticity is proportional to
the slope of each curve at the equilibrium interatomic
separation r0 .

54. Plastic Deformation
For most metallic materials, elastic deformation persists only to strains of about
0.005. As the material is deformed beyond this point, the stress is no longer proportional
to strain (Hooke’s law ceases to be valid), and permanent, non-recoverable, or
plastic deformation occurs.
Figure 1 :-
Stress–
strain
behavior
for
a metal
showing
elastic and
plastic
deformati
ons .
Figure 2 :-
Representative
stress–strain
behavior
found for some
steels
demonstrating
the yield point
phenomenon.

55. Plastic Deformation
From an atomic perspective, plastic deformation corresponds to the breaking
of bonds with original atom neighbors and then reforming bonds with new neighbors
as large numbers of atoms or molecules move relative to one another; upon
removal of the stress they do not return to their original positions.

56. Measurement of Mechanical
Properties
1. HARDNESS TESTS
2. COMPRESSION TESTS
3. TENSION TESTS
4. IMPACT TESTS

57. Hardness Tests
There are three general types of hardness measurements :-
1) Scratch hardness
• The ability of material to scratch on one another
• Important to mineralogists, using Mohs’scale 1= talc, 10 = diamond
• Not suited for metal annealed copper = 3, martensite = 7.
2) Indentation hardness
• Major important engineering interest for metals.
• Different types : Brinell, Meyer, Vickers, Rockwell
hardness tests
3) Rebound hardness
• The indentor is dropped onto the metal surface and the
hardness is expressed as the energy of impact.

58. Moh’s Hardness Scale
The Moh's hardness scale for minerals has been used since 1822. It simply
consists of 10 minerals arranged in order from 1 to 10. Diamond is rated as
the hardest and is indexed as 10; talc as the softest with index number 1. Each
mineral in the scale will scratch all those above it as follows:

59. Indentation Hardness Tests
1.Rockwell Test
2.Brinell’s Test
3.Meyer’s Test
4.Vicker’s Test
5.Knoop Microhardness Test
6.Vicker’s Microhardness Test

60. Rockwell Test
• The Rockwell hardness test method consists of indenting the test material
with a diamond cone or hardened steel ball indenter.
• The indenter is forced into the test material under a preliminary minor
load F0 usually 10 kgf.
• When equilibrium has been reached, an indicating device, which follows
the movements of the indenter and so responds to changes in depth of
penetration of the indenter is set to a datum position.
• While the preliminary minor load is still applied an additional major load
is applied with resulting increase in penetration .
• When equilibrium has again been reached, the additional major load is
removed but the preliminary minor load is still maintained.
• Removal of the additional major load allows a partial recovery, so reducing
the depth of penetration .
• The permanent increase in depth of penetration, resulting from the
application and removal of the additional major load is used to calculate
the Rockwell hardness number.

61. Rockwell Test
HR=E-eWhere :
• F0 = preliminary minor load in kgf
• F1 = additional major load in kgf
• F = total load in kgf
• e = permanent increase in depth of penetration due to major load measured in units of 0.002 mm
• E = a constant depending on form of indenter: 100 units for diamond indenter, 130 units for steel ball indenter
• HR = Rockwell hardness number
• D = diameter of steel ball
Rockwell Principle

62. Brinell’s Test
J.A. Brinell introduced the first standardised indentation-hardness test in 1900. The
Brinell hardness test consists in indenting the metal surface with a 10-mm diameter
steel ball at a load range of 500-3000 kg, depending of hardness of particular
materials.
• The full load is normally applied for 10 to 15 seconds in the case of iron and steel and
for at least 30 seconds in the case of other metals.
• The diameter of the indentation left in the test material is measured with a low
powered microscope.
• The Brinell harness number is calculated by dividing the load applied by the surface
area of the indentation.

63. Meyer’s Test
Meyer suggested that hardness should be expressed in terms of the mean
pressure between the surface of the indenter and the indentation, which is
equal to the load divided by the projected area of the indentation.
Meyer hardness is therefore expressed as follows :-

64. Vicker’s Test
• To convert HV to MPa we multiply by
9.807
• To convert HV to GPa we multiply by
0.009807
• The Vickers hardness test method consists of
indenting the test material with a diamond indenter,
in the form of a right pyramid with a square base and
an angle of 136 degrees between opposite faces
subjected to a load of 1 to 100 kgf.
• The full load is normally applied for 10 to 15 seconds.
• The two diagonals of the indentation left in the
surface of the material after removal of the load are
measured using a microscope and their average
calculated.
• The area of the sloping surface of the indentation is
calculated
• The Vickers hardness is the quotient obtained by
dividing the kgf load by the square mm area of
indentation.

65. Microhardness Test
• The term microhardness test usually refers to static indentations
made with loads not exceeding 1 kgf.
• The indenter is either the Vickers diamond pyramid or the Knoop
elongated diamond pyramid.
• The procedure for testing is very similar to that of the standard
Vickers hardness test, except that it is done on a microscopic scale
with higher precision instruments.
• The surface being tested generally requires a metallographic finish;
the smaller the load used, the higher the surface finish required.
• Precision microscopes are used to measure the indentations; these
usually have a magnification of around X500 and measure to an
accuracy of +0.5 micrometres.
• Also with the same observer differences of +0.2 micrometres can
usually be resolved.

66. Knoop Microhardness Test
The Knoop indenter
• The Knoop indenter (diamond shape)
is used for measuring in a small
area, such as at the cross section of the
heat-treated metal surface.
• The Knoop hardness number KHN is the ratio of
the load applied to the indenter, P (kgf) to the
unrecovered projected area A (mm2)
Where:
F = applied load in kgf
A = the unrecovered projected area of the indentation
in square millimetres
L = measured length of long diagonal of indentation in mm
C = 0.07028
= Constant of indenter relating projected area of the
indentation to the square of the length of the long
diagonal.

67. Vicker’s Microhardness Test
1. This is same as Vickers hardness except that the applied load is much smaller so as to
cover a small area.
2. The applied load range is 1 – 100 g ( Microhardness Test Range )

68. Compression Tests
• Compression test is used to obtain the mechanical
properties and is the basis of acceptance and refusal
of brittle non-metallic and other materials that have
very low strength in tension like concrete , wood ,
masonry ,etc .
• Bearing blocks are used to ensure the load is applied
to the specimen .
• Spherical loading heads are used to avoid applying
the load at a single point if the loading surfaces are
at a small angle .

69. Compression Tests
Compression Test Setup

70. Behaviour of metals under
compression tests

71. Tension Tests
• Figure : Schematic representation of
the apparatus used to conduct
tensile stress-strain tests .
• The specimen is elongated
by the moving crosshead.
• Load cell and extensometer measure,
respectively, the magnitude of the
applied load and the elongation .
Figure :
Standard specimen used for
tensile testing.

72. Stages in tension testing
1. Elastic deformation 2. Plastic deformation
3. Necking 4. Fracture

73. Tension Testing
Stress- Strain curves for tensile testing

74. Impact Tests
Izod Impact Test
• In the Izod impact test, the test piece
is a cantilever, clamped upright in an
anvil, with a V-notch at the level of
the top of the clamp.
• The test piece is hit by a striker
carried on a pendulum which is
allowed to fall freely from a fixed
height, to give a blow of 120 ft lb
energy.
• After fracturing the test piece, the
height to which the pendulum rises is
recorded by a slave friction pointer
mounted on the dial, from which the
absorbed energy amount is read.
Standard Specimen
for the test
Diagram

75. Impact Tests
Charpy’s impact test
The principle of the test differs from that of the Izod test in that the test piece is
tested as a beam supported at each end; a notch is cut across the middle of one
face, and the striker hits the opposite face directly behind the notch.
Sample specimen for Charpy’s impact test Apparatus

76. Bibliography
• Materials Science and Engineering An
Introduction by William D. Callister, Jr .(John
Wiley & Sons, Inc.).
• The Internet .