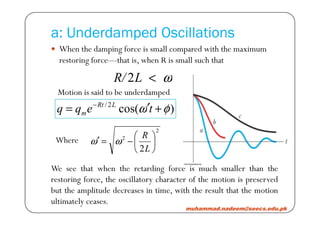
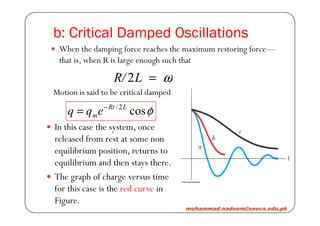
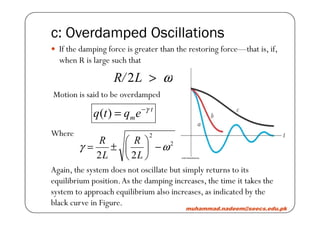
1) The document discusses electromagnetic oscillations in LC circuits. It describes how the electric and magnetic energy oscillate between the inductor and capacitor over time, with the total energy remaining constant. 2) Damped oscillations in an LC circuit with resistance R are also examined. The type of damping (underdamped, critically damped, or overdamped) depends on the ratio of R to other circuit parameters. 3) Forced oscillations occur when an external periodic force supplies energy to compensate for losses, maintaining a steady oscillation amplitude. Resonance effects occur near the natural frequency of the system.

1. Muhammad Nadeem
School of Electrical Engineering &Computer Sciences
ma
F =
Electromagnetic Oscillations
∂
=
+
∂
−
ψ
ψ
ψ
2
2
hf
E =
Muhammad Nadeem
School of Electrical Engineering &Computer Sciences
muhammad.nadeem@seecs.edu.pk
2
mc
E =
t
B
E ∂
−∂
=
×
∇ /
ma
F =
Physics
20th Century 21st Century
t
i
V
x ∂
∂
=
+
∂
∂
−
ψ
ψ
ψ
h
h 2
2
2
hf
E =
o
ε
ρ /
=
•
∇ E
mv
P =
P
r
L ×
= h
≈
∆
∆ P
x.
0
=
•
∇ B
t
E
j
B ∂
∂
+
=
×
∇ /
o
o
o ε
µ
µ
P
h
=
λ
h
G
k
o
ε
o
µ
R
c

2. Electromagnetic Oscillator
0
=
+
c
q
dt
di
L
Consider a LC circuit with no resistance and zero emf applied. By
Kirchhoff's voltage rule,
0
2
=
+
q
q
d
L
C
0
2
=
+
Lc
dt
The solution of above 2nd order homogenous ODE with constant
coefficients will be
)
cos( φ
ω +
= t
q
q m
LC
/
1
=
ω
Where is the maximum charge on capacitor, is the phase
constant and is the angular frequency.
m
q φ
muhammad.nadeem@seecs.edu.pk

3. Electric energy stored in LC circuit is
)
(
cos
2
2
1 2
2
2
φ
ω +
=
= t
C
q
q
C
U m
E
1
1
2

 dq
Electric energy is stored in the
electric field inside capacitor
Magnetic energy stored in LC circuit is
)
(
sin
2
)
(
sin
2
1
2
1
2
1
2
2
2
2
2
2
2
φ
ω
φ
ω
ω
+
=
+
=






=
=
t
C
q
t
q
L
dt
dq
L
Li
U
m
m
B
m
k
=
∴ 2
ω
Magnetic energy is stored in the
magnetic field inside Inductor
muhammad.nadeem@seecs.edu.pk

4. Both, UE and UB, oscillates with time and have a maximum
value of
During the motion both, UE and UB vary between zero and
maximum value.
The total energy of the oscillator remains constant at every
time.
C
qm
2
2
time.
C
q
t
C
q
t
C
q
U
U
E
m
m
m
B
E
2
)
(
cos
2
)
(
cos
2
2
2
2
2
2
=
+
+
+
=
+
=
φ
ω
φ
ω
muhammad.nadeem@seecs.edu.pk

5. E
K
U
Energy versus time at ϕ=0
)
(
cos
2
2
2
t
C
q
U m
E ω
=
)
(
sin
2
2
2
t
C
q
U m
B ω
=
C
q
E m
2
2
=
muhammad.nadeem@seecs.edu.pk

6. Consider an oscillating LC circuit with L=12mH and C=1.7µF.
(a) what value of charge is present on the capacitor when the
energy is shared equally between electric and magnetic field?
(b) At what time t will this condition occur? Assume capacitor is
fully charged at t=0
Since
(a)
C
q
E m
2
2
=
C
q
UE
2
2
=
So
C
2 C
2
C
q
C
q
E
U m
E
2
2
1
2
2
1
2
2
=
⇒
=
2
m
q
q =
muhammad.nadeem@seecs.edu.pk

7. (b) If capacitor is fully charged at t=0 then
)
cos(
2
)
cos(
t
q
q
t
q
q
m
m
m
ω
ω
=
=
t
ω
1
)
cos( =
s
LC
t
t
t
µ
π
π
ω
ω
110
4
4
/
2
1
)
cos(
=
=
=
=
muhammad.nadeem@seecs.edu.pk

8. Damped Oscillator
A resistance R is always present in LC circuit.When we take this
resistance into account,
0
=
+
+
c
q
iR
dt
di
L
0
2
2
=
+
+
LC
q
dt
dq
R
dt
q
d
L
C
R
0
2
=
+
+
LC
dt
R
dt
The solution of above 2nd order homogenous ODE with constant
coefficients will be
)
cos(
2
/
φ
ω +
′
= −
t
e
q
q L
Rt
m
2
2
)
2
/
( L
R
−
=
′ ω
ω
Where is the maximum charge on capacitor, is the phase
constant and is the angular frequency.
m
q φ
muhammad.nadeem@seecs.edu.pk

9. a: Underdamped Oscillations
When the damping force is small compared with the maximum
restoring force—that is, when R is small such that
ω
L
R/
2
Motion is said to be underdamped
)
cos(
2
/
φ
ω +
′
= −
t
e
q
q L
Rt
m
Where
2
2
2






−
=
′
L
R
ω
ω
)
cos( φ
ω +
′
= t
e
q
q m
We see that when the retarding force is much smaller than the
restoring force, the oscillatory character of the motion is preserved
but the amplitude decreases in time, with the result that the motion
ultimately ceases.
muhammad.nadeem@seecs.edu.pk

10. b: Critical Damped Oscillations
When the damping force reaches the maximum restoring force—
that is, when R is large enough such that
ω
L
R/ =
2
Motion is said to be critical damped
φ
cos
2
/ L
Rt
me
q
q −
=
In this case the system, once
released from rest at some non
equilibrium position, returns to
equilibrium and then stays there.
The graph of charge versus time
for this case is the red curve in
Figure.
φ
cos
me
q
q =
muhammad.nadeem@seecs.edu.pk

11. c: Overdamped Oscillations
If the damping force is greater than the restoring force—that is, if,
when R is large such that
t
e
q
t
q )
( γ
−
=
ω
L
R/
2
Motion is said to be overdamped
t
me
q
t
q )
( γ
−
=
2
2
2
2
ω
γ −






±
=
L
R
L
R
Again, the system does not oscillate but simply returns to its
equilibrium position.As the damping increases, the time it takes the
system to approach equilibrium also increases, as indicated by the
black curve in Figure.
Where
muhammad.nadeem@seecs.edu.pk

12. Consider RLC circuit having L=12mH, C=1.6µF and R=1.5Ω.
After what time t will the amplitude of the charge oscillations
drop to one half of its initial value?
L
Rt
e L
Rt
2
ln
2
/
2
1
2
/
−
=
−
=
−
In RLC circuit, amplitude of charge oscillations will be half if
s
t
R
L
t
L
Rt
011
.
0
2
ln
2
2
ln
2
/
=
=
−
=
−
muhammad.nadeem@seecs.edu.pk

13. In any case in which resistance is present, whether the
system is overdamped or underdamped, the energy of
the oscillator eventually falls to zero. The lost
the oscillator eventually falls to zero. The lost
ELECTROMAGNETIC energy dissipates into heat.
muhammad.nadeem@seecs.edu.pk

14. It is possible to compensate for energy
loss in a damped system by applying an
external force that does positive work
on the system.
At any instant, energy can be put into
the system by an applied force that
Forced Oscillator
L
C
R
~
the system by an applied force that
acts in the direction of motion of the
oscillator.
The amplitude of motion remains constant if the energy input per
cycle exactly equals the energy lost as a result of damping.Any
motion of this type is called forced oscillation.
muhammad.nadeem@seecs.edu.pk

15. A common example of a forced oscillator is a damped oscillator
driven by an external force that varies periodically, such as
Where is the angular frequency of the applied periodic force
)
cos(
0 t
ω
ξ
ξ ′
=
After a sufficiently long period of time, when the energy input per
ξ
=
+
+
LC
q
dt
dq
R
dt
q
d
2
2
ω′
After a sufficiently long period of time, when the energy input per
cycle equals the energy lost per cycle, a steady-state condition is
reached in which the oscillations proceed with constant amplitude.At
this time, when the system is in a steady state, the solution of above
Equation is
)
cos( φ
ω +
′
= t
q
q m
( )
2
2
2
2
/





 ′
−
−
′
=
L
R
L
qm
ω
ω
ω
ξo
muhammad.nadeem@seecs.edu.pk

16. Because an external force is driving it, the motion of the forced
R=0; Undamped
Small R
Large R
Because an external force is driving it, the motion of the forced
oscillator is not damped.The external agent provides the necessary
energy to overcome the losses due to the retarding force. Note that
the system oscillates at the angular frequency of the driving force.
For small damping, the amplitude becomes very large when the
frequency of the driving force is near the natural frequency of
oscillation.The dramatic increase in amplitude near the natural
frequency ω is called resonance, and for this reason ω is sometimes
called the resonance frequency of the system
ω′
muhammad.nadeem@seecs.edu.pk